ここまでの熱力学によれば，状態は自由エネルギーまたはエントロピーによって序列がつけられることがわかりました．自由エネルギーがわかれば，系から自由に取り出せる仕事がわかります．つまり，使える「資源」の限界を教えてくれます．

平衡状態は熱力学ポテンシャルの極値をとるような状態として決まりますが，熱力学ポテンシャルの凸性によって，平衡状態とは安定な世界であることが保証されました．しかし，物理系が実際に「機能」をしているときというのは，系は平衡状態にはなく，非平衡状態に駆動されています．もっとも身近な（かつ複雑な）例としては私たち生命で，明らかに生命は非平衡状態であって，そのためにエネルギーを常に消費しています．そもそも私たちは太陽からのエネルギーが注ぎ非平衡に維持された世界に生きていて，身の回りを見渡してみると，平衡状態というのはむしろ例外的です．

それでも，平衡状態の熱力学が有用なのは，ほとんどの場合局所的に見れば平衡状態と思うことができるからです．非平衡状態も平衡状態を頼りに考えていくのが自然な方法でしょう．ここでは，もっとも簡単な非平衡状態として，平衡状態からわずかにずれた場合を考えます．この場合，非平衡状態は平衡状態に向かって不可逆的に変化していくことになりますが，その過渡的な現象を応答関数によって記述する方法を考えます．よって，これからは時間が変数に入ってきます．応答関数の理論的な導出は統計力学の仕事になるので，今回は非平衡統計力学のための布石としての話といえます．

線形関係式

外力を系に加え，流れが駆動されるときを考えます．流れとは，示量変数の時間変化のことで，

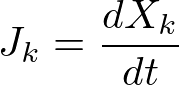
とあらわします．外力が小さく，平衡の近くで議論できる場合，現象論的に外力と流れの間に線形の関係式

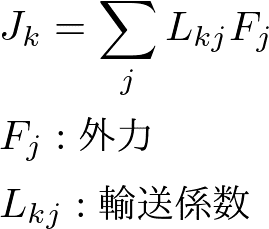
が成り立つことが期待されます．添え字は種類の違いを区別するためのものです．力についている係数は輸送係数といいます．輸送係数はは一般に二階のテンソルで表されています．これは，交差効果，つまりある種類の力がいくつかの種類の流れを駆動することがあることを示しています．たとえば，温度勾配による熱的な力は，熱流だけでなく，物質の流れや電流なども駆動することができ，それぞれ交差拡散，熱電効果（ゼーベック効果・ペルチェ効果）と呼ばれ知られています．

交差効果のない簡単な場合のこのような現象論的関係式の例として，以下があげられます．

オームの法則（電気伝導）

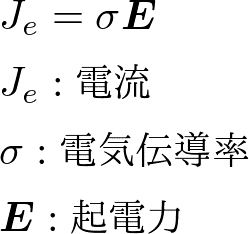
フィックの法則（拡散）

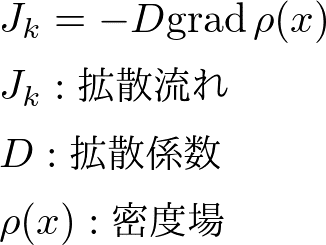
フーリエの法則（熱伝導）

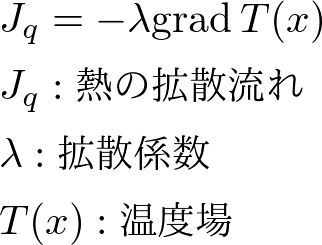
などなどです．電気伝導率や拡散係数が輸送係数に対応します．また，交差効果を含む熱電現象は

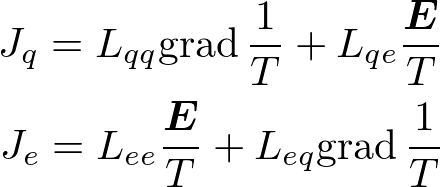
という形で書けます．これらの式において，外力は，電場や密度や温度といった体積当たりの示量変数または示強変数が空間的に分布していると考えて出てくるものになっています．系全体としては非平衡状態ですが，局所的には平衡状態と見て，各場所に熱力学的な量を割り当てているわけです．

輸送係数を用いた線形関係式は，右辺と左辺は同時刻の量を表していますが，これは流れを力に対して瞬時に応答するような現象として見ていることを意味します．このように，過去の状況によらず，今の力だけで応答が決まるような性質を，マルコフ的であるといいます．

非マルコフ過程への拡張

現象論的な式は，理論の適用範囲が広いほうが価値が高い．マルコフ的な関係が成り立たない場合にも式を拡張しようと試みます．実際，時間の精度を細かくしていくと，力に対して流れの応答が遅れてくる現象が見られます．この遅れの効果が無視できないような時間精度で見るときを考え，先ほどの現象論的線形関係式を拡張すると，

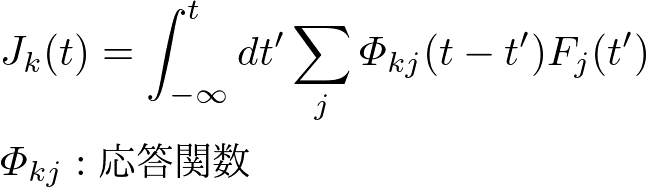
という非マルコフ的な形にできます．右辺の積分は畳み込み積分と呼ばれる積分で，過去の力に対する応答の「記憶」を現在の時点までですべて足し合わせることで，現在の応答を求める形です．輸送係数の代わりに現れた係数は，応答関数と呼ばれます．

過去の力は長い時間経てば消えるのが普通なので，応答関数は

を満たすべき，としておきます．

以上の議論では前提として，線形性に加えて，因果性を仮定しています．因果性とは，流れの応答（結果）は力（原因）よりも前には生じないという性質です．これは積分の中に過去の力のみ現れていて，未来の力は入っていないところに現れています．

力の時間変化が緩やかな場合，積分の中の力の引数にとってある時刻を過去の時刻でなく現在時刻で置き換えてよく，

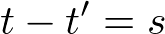
と変数変換すれば

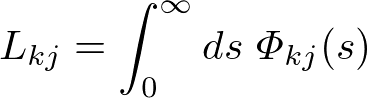
となり，マルコフ過程に戻ることが確かめられます．

応答関数を使った記述で線形関係式をやや一般化できました．

応答関数と緩和関数

不可逆現象を具体的に見るために，ある時刻までかけておいた力を突然取り除く場合を考えてみます．その時点までは，力のかかったもとでの平衡状態にあった系が，力が除かれた後は，力のかかっていない新しい平衡状態へと向かって緩和していきます．

加えていた力を

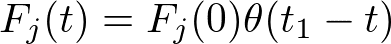
と書きます．右辺に現れた関数はステップ関数で，

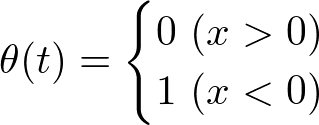
という関数です．これを畳み込み積分に代入すれば，力を切った後の応答は，

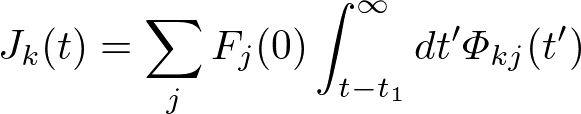
と書けることがわかります．右辺の積分

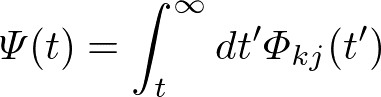
は緩和を表す関数なので，これを緩和関数と呼びます．

緩和関数と応答関数は積分と微分の関係にあることがわかります．したがって，加えていた力の初期値がわかっている場合，緩和と応答のどちらかがわかれば他方もわかる関係であり，緩和と応答は等価な情報を持っています．

複素感受率とエネルギー散逸

非マルコフ的な線形関係式をフーリエ変換すると

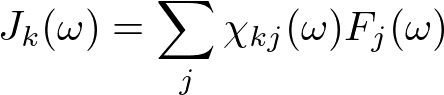
と簡単な式が得られます（この結果を畳み込み定理といいます）．
ただし，

と定義しました．（流れや力のフーリエ変換も同様の定義ですが，記号はもとの流れや力と区別せず，引数のみによって区別したことには注意してください．）この応答関数のフーリエ変換を複素感受率（または複素アドミッタンス，周波数応答関数）といいます．（注: フーリエ変換でなくラプラス変換した場合は伝達関数といいます．）

力が周期的な場合，たとえば

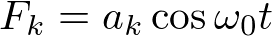
と書けるとき，畳み込み積分によって，応答を計算すると

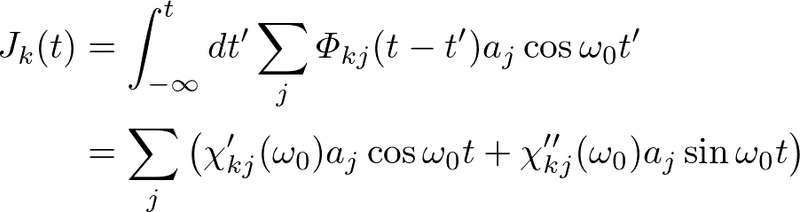
となります．ここで，複素感受率の実部と虚部をそれぞれ

と置きました．（計算過程は省略したのでできそうな人はやってみてください．3行くらいの計算でできると思います．）

一般に，仕事率は，力と流れの積で書けるので，一周期の後に外力が系にした仕事は

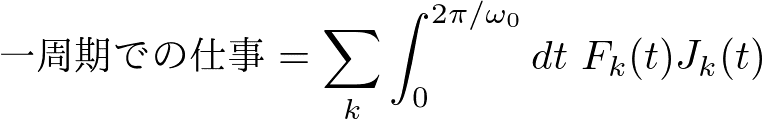
と書けます．力と流れに具体的なものを代入して計算すると

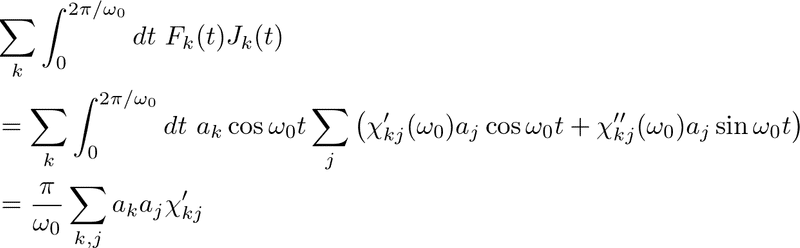
となります．一周期の時間平均をとったものは，

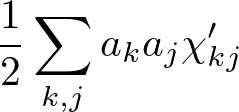
となります．

系が周期的な運動をするとき，一周期後には元の状態に戻っていますから，系のエネルギーは最初と最後で変わりません．熱力学第二法則の内容は，系にした仕事のすべては自由エネルギーに蓄えられず，一部分は環境に散逸してしまうということでした．したがって，外力が一周期の間にした仕事は決して負ではないということがいえて，

となっています．この単位時間あたりに損失したエネルギーをパワーロスといいます．外力によって流れが駆動される場合，複素感受率の実部がパワーロスに結びついていることがここからわかります．

まとめ

今回言いたかったことは，系が少しだけ非平衡状態にあるときは，系の応答関数がわかれば過渡的な非平衡状態が記述できるということですが，その応答関数を調べるためには，力を切った後の系の緩和を測定するか，周期的な力を連続的に加えたときのパワーロスを調べればよいということになります．

ところで，この現象論をミクロな運動方程式から導出できないでしょうか？応答関数を系のミクロな性質から導けないでしょうか？実は，応答関数は，平衡状態のミクロなゆらぎを観察すれば求めることができるのです．これはアインシュタインやナイキストが初めて示した揺動散逸定理と呼ばれるもののより一般的な内容で，久保亮五によって示されました．これを示すのは統計力学の仕事になります．

（注: 複素感受率の実部と虚部の一方がわかれば，実はもう一方もわかります．クラマース・クローニッヒの関係と呼ばれる関係式によるものですが，物理的には因果律に原因を求めることができます．詳しくは別の節で証明したいと思っています．）

コラム（光学の分散・吸収）

複素感受率の実部を分散，虚部を吸収と呼ぶことがあります．この用語は光学に由来します．（最初聞いたとき，どういう意味だろうと私は思いました．）ある周波数の光をある媒質に入射したとき，誘電率は，

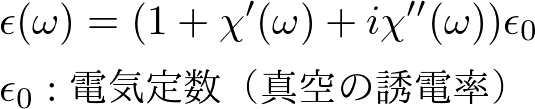
と応答します．すると波数は，

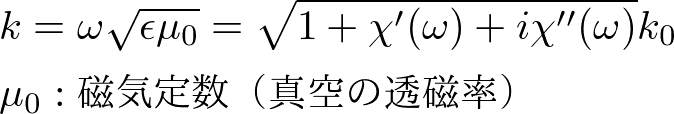
と応答します．感受率が小さいとき，

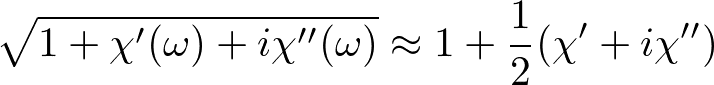
と近似でき，したがって，波動の空間分布は

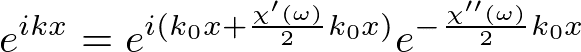
となります．この式をよく見ると，感じる屈折率が

となっていて，また

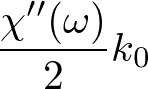
という係数で減衰していくような波を表しています．つまり，複素感受率の実部は屈折率の波長依存性に結びついていて，プリズムで異なる波長の光を分散させる現象が説明されます．一方，複素感受率の虚部は媒質が光を吸収して減衰する現象を説明します．こういうわけで，複素感受率の実部と虚部をそれぞれ分散，吸収と呼びます．