2「典型性とミクロカノニカル分布」の補足です．

典型性を要請して，アンサンブルに含まれる代表点はほとんど確実に平衡状態に対応する，としました．「ほとんど確実に」とは何かをもう少しきちんと説明します．

熱力学極限

十分大きなサイズの系では，熱力学的な状態は少数の変数で指定されることが知られています．平衡統計力学の理論は，系のサイズが十分大きいような極限で，この熱力学に漸近していくような理論として作ることを目指します．

系のサイズを大きくすることは，力学では粒子数を増やすことに対応します．熱力学的な状態を変えないように粒子数を増やすには，系の密度が変わらないように，エネルギーや体積といった示量変数も粒子数に比例して増加させていくのが自然です．この根拠を以下に見ていきましょう．

エネルギー・体積・粒子数を変数として用いるとき，熱力学では系の状態は，

というふうにエントロピーをエネルギー・体積・粒子数の関数で表したものによって完全に指定されます（この記事を参照）．ここで，エントロピーには示量性があるので，

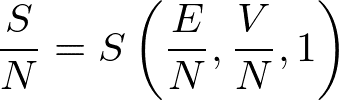
と書くことができます．このように，熱力学的な状態は本質的には二つの密度で指定されます．したがって，この二つの密度を保っていれば，熱力学的な状態を変えずに，系のサイズだけ大きくする極限をとることができます．

というわけで，統計力学では常に，

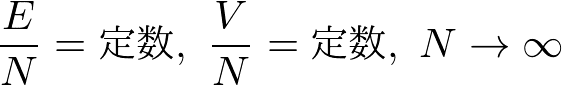
という極限をとって考えます．これを熱力学極限といいます．

ほとんど確実にの意味

「アンサンブルに含まれる代表点はほとんど確実に平衡状態に対応する」というのは，熱力学極限において，非平衡状態に対応するような特殊な状態は確率０でしかアンサンブルに含まれておらず，典型的な状態が確率１で含まれていますよ，という意味です．熱力学極限において典型性が成り立つと要請するのです．

（注: 確率０といっても，まったく含まれていないという意味ではありません．たとえば，実数の集合の中からある数を選ぶとき，整数を選ぶ確率は０ですが，もちろん整数は存在はしていますし，しかも無限に存在しています．）

（注の注: 上で整数を選ぶ確率が０なのをちゃんと説明すると，実数の濃度が無限なのに対して，整数の濃度は可算だからです．実数の濃度が無限であることは，カントール（Cantor）の対角線論法によって証明されます．）