【統計力学3】状態数と熱力学的重率【エネルギー幅の任意性】
統計力学では,アンサンブル平均をとることを物理量の計算手段とするわけですので,アンサンブルに含まれる状態の数を数えることが本質的に重要となります.今回は状態の数え方について考察しましょう.
状態数
まず,状態数(総状態数と呼ぶ教科書もあります)というものを定義します.(確率論でいうところの累積分布関数に似たものです.)
状態数は,「あるエネルギー以下の状態の数」で定義します.ただし,古典力学では状態は位相空間上で連続に変化するものですから,「数」と言われても困ってしまいます.しかし,リウビルの定理があるので,一様分布を仮定すれば「数」は「位相空間の体積」で測ることができます.というわけで,状態数を次のように,位相空間をあるエネルギー以下の部分で積分したものによって定義します.

つまり,等エネルギー面に囲まれた体積です.ただし,記号の意味は

です.ここで,体積をただの数に対応させるために「エネルギー×時間」の次元を持った(今のところ物理的意味はよくわからない)定数で割っています.この定数はプランク(Planck)定数と呼ばれます.
具体例
統計力学ではモデルを立てて計算して,熱力学を再現することを見るので,具体例を考えることは重要です.ここでは理想気体と連成振動子について,状態数を計算してみましょう.
(注: これらの例は,可積分系です.可積分系は緩和せず,熱力学を再現しませんから,これらに統計力学を適用してよいものか悩みます.しかし,緩和した後のことを計算したいだけなので,別によいのです.もし相互作用が小さい系なら,これらの理想化したモデルで「平衡状態の」物理量を近似計算できるでしょう.もちろん,緩和過程を考えるには,弱くてもいいから相互作用を入れる必要がありますが,これはずっと難しい問題です.)
(1) 理想気体
理想気体のハミルトニアンは,気体粒子同士に相互作用がないとして,各粒子の運動エネルギーの和
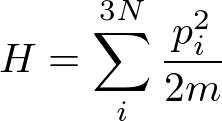
で表されます.したがって,状態数は
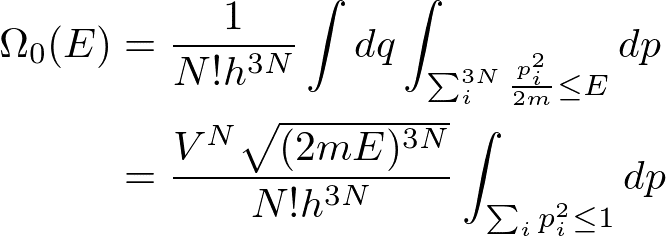
と計算することができます.二行目の式に行くときに,座標での積分は体積を与えることを用いています.また,積分の変数変換をして積分の範囲を簡単にしました.
ここで,粒子数の階乗で割っていることが気になるかと思います.粒子の入れ替えに関して,状態が区別可能と考えればこのファクターは要りませんが,粒子の入れ替えは区別できないと考えて,このファクターで割っています.状態数の数え方にはこのような任意性があるのですが,このように粒子の入れ替えは区別しないで数えるのが,実は熱力学的に正しい結果を与えるのです.そのことは後に統計力学と熱力学の対応を見るときに確認します.
この積分の範囲をよく見ると,この積分は「半径1の球(単位球)の体積」を表していることがわかります(ただし多次元の球です).単位球の体積は一般に

と書けることが数学的に知られています.ここで,分母に出てきた関数はガンマ関数といわれ,
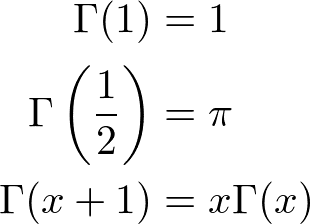
という性質を満たしています.実はガンマ関数は,階乗を実数の範囲に拡張したものになっています(三つ目の性質をよーく見るとわかります).すなわち

となっています.
統計力学は漸近理論ですから,近似を適切に用いることが大切です.ガンマ関数については,スターリング(Stirling)の公式という近似式が知られています.統計力学では,

という形でスターリングの公式をよく用います.また,これをおおらかに指数を取って,
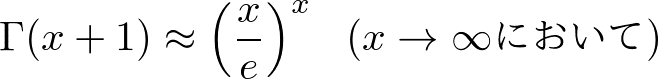
とするのは,本当は数学的には良くありませんが,後でわかるように統計力学の計算をするときは,いつも状態数の対数をとることになるので,この程度の粗い近似を許してもらうことにしましょう.
(注: 上で用いた記号について,

は,「漸近する」というちゃんとした意味で用いています.一方

は,「だいたい等しい」という意味で割と適当に用いています.対数をとれば,ちゃんとした意味に戻せるので,まあいいか,というのが今の話です.漸近の意味やランダウの記号についてはこちらの記事を参照ください.)
というわけで,状態数は熱力学極限において,おおらかに
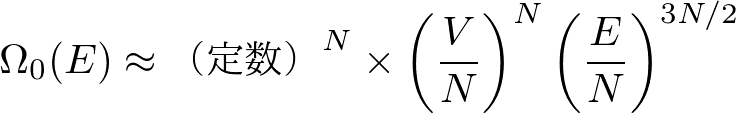
となります.定数の部分は次元をキャンセルしてくれる以外にたいした意味がないので,まとめてこのように書くと見やすい.
ここで,注目すべきは,状態数が密度の関数になっていることです.(ただし,普通の体積あたりの密度ではなく,一粒子あたりの密度で書きました.普通の密度で書くことももちろんできます.どちらでも同じことです.)そして,状態数が密度の関数になったのは,粒子数の階乗で割ったことのおかげであることに注意しておきましょう.
(2) 連成振動子
たくさんの粒子がばねで繋がった系を連成振動子といいます.ここでは下図のような一次元の連成振動子を考えます.
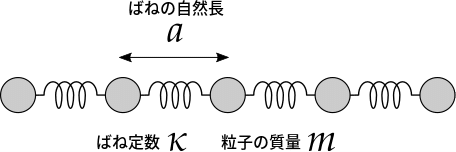
このような連成振動子のハミルトニアンは
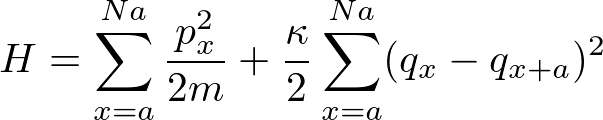
と書かれます.ここでの座標は,自然長からのずれとしています.相互作用の項があってややこしそうですが,これはうまく座標を変換してやると,
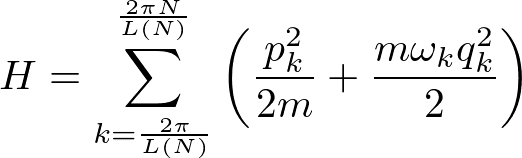
となり,なんと独立な調和振動子の和と等価であることが示せます.この特別な空間では,調和振動子は波数(wave number)
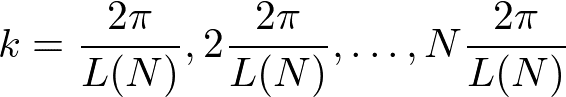
でラベルされています.ただしここで,
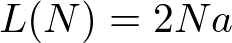
は連成振動子の長さの2倍で定義しました.また,ある波数に対応する固有振動数(eigenfrequency)は
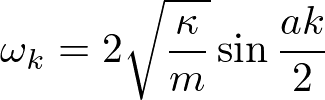
となります.
このように,連成振動子はうまい座標系に変換すると,相互作用をうまく解きほぐして,多数の調和振動子の問題に直せるのですが,そのことの詳しい説明をしだすと,今回の主題から離れてしまいます.この記事では,これは数学的には行列の固有値問題を解くことに対応していて,特にフーリエ変換していることと同じである,と言うにとどめておき,詳しくはまた別の記事で書くことにしましょう.
調和振動子の問題に置き換えることができたので,状態数は
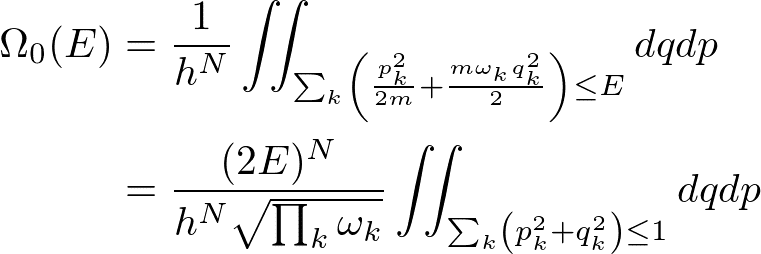
と計算できます.粒子はここでは入れ替わらないので粒子数の階乗で割るファクターは出てきません.分母に厄介そうな積が出てきますが,粒子数を無限に飛ばす極限をとっても収束するので,ただの定数と思ってよい.
やっぱり球の体積の項が出てくるので,先の例と同じようにして,球の体積を求めます.熱力学極限において,スターリングの公式をおおらかに使うと,

となります.ここでも,状態数が密度の関数になっています.
熱力学的重率
一方,アンサンブルとは,等エネルギー面の上に一様に分布した代表点の集合でした.状態数よりもむしろこちらを考えなければなりません.等エネルギー面の上の状態の数は熱力学的重率と呼ばれます.熱力学的重率は,状態数を用いて,
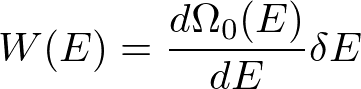
と書けます.右辺の微分係数は状態密度と呼ばれ
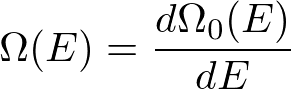
と書くことにします.(状態数が累積分布関数なら,状態密度は確率密度関数のようなものです.)ただし,エネルギーに幅がないと体積がゼロになってしまって数が測れないので,
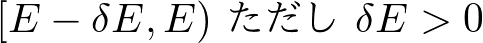
という適当なエネルギーの区間内での状態の数を数えることにしています.
(注: 熱力学的重率は教科書によって呼び方が違います.これを単に「状態数」と言うものもあります.「統計的重率」「許される状態数」「微視的状態数」「配置数」などの用語を見たことがあります.)
エネルギーの幅について
熱力学的重率の定義にエネルギー幅が出てきましたが,幅のとり方によって熱力学的重率の大きさは変わってしまいます.ですからエネルギー幅を導入することは気持ちの悪い要素です.このような人為的に導入したエネルギー幅が理論の最後まで残っては絶対にいけません.
しかし,実はこのエネルギー幅は何でもよいことがわかるので安心します.なんと,極端に,
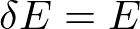
としてもよいのです.そうすると結局,
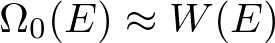
が十分な精度で(対数をとると熱力学極限で無視できる精度で)成り立ち,状態数を使おうが熱力学的重率を使おうがどちらでもよいことになります.
ずいぶんいい加減に思われると思います.なぜそんないい加減なことをしていいのでしょうか?もう一度先ほどの例を振り返ってみましょう.状態数は理想気体については
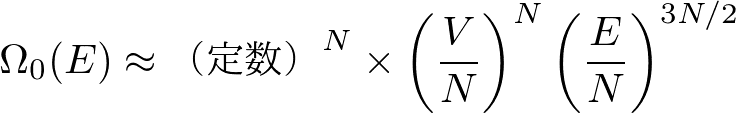
で,連成振動子については

となるのでした.このように,状態数は
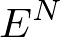
くらいの程度でエネルギーに依存しています.状態密度は,状態数のエネルギーでの微分ですから,エネルギーの次元が一つ下がって,
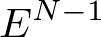
くらいになります.しかし,粒子数は,猛烈にもの凄く多い状況を考えるので,このマイナス1にほとんど意味はありません.ですから,
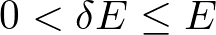
の範囲なら,どんな値をとっても,熱力学的重率は結局のところ状態数と大して変わりません.したがって,エネルギーの幅はこの範囲なら何でもよいのです.
これは空間の次元が大きくなると,体積のほとんどは表面に集中していることに由来します.そのために,一般的に,等エネルギー面の内部全体の体積は,表面付近の体積をとってもほとんど変わりません.その結果,状態数と熱力学的重率はどちらでも同じくらいになるのです.
(私は餃子が好きですが,おいしく餃子を食べていられるのも,生きている空間が3次元なことのおかげですね.もしも大きな次元の空間に生きていたら,餃子の体積のほとんどが皮ということになってしまいますから.餃子のおいしさは皮と餡の絶妙なバランスにあります.)
今回のまとめ
アンサンブルに含まれる状態の数(熱力学的重率)は,等エネルギー面で囲まれた位相空間の体積で測ったもの(状態数)でよい.
_____________________
更新履歴
Mar. 23, 2020 ちょっとした都合により状態数を表す記号を\Omegaから\Omega_0に変更しました.
クオリティの高いノートをたくさん書けるように頑張ります!
