1925年にヴェルナー・ハイゼンベルクが奇妙な論文を出しました。

原子における電子の軌道について、です。

それまでの電子軌道の計算は、誰のものも不完全に終わっていました。

当時とある有力説があったのですが、それも使えないと判明しました。

ハイゼンベルク（当時23歳）はとうとう開き直りました。「だいたい電子の周回軌道だなんて誰がそれを確認したっていうんだ？顕微鏡でそれが見えたっていうのかよ。ええいこうなったら周回軌道のイメージをかなぐり捨てて、観測データとつき合わせて確認されている値オンリーで数式作ってまえ！」

そして彼が書き上げたのは、∑と数列が ∞ とともに並ぶ、わけのわからない論文でした。

それを送られた師匠筋のマックス・ボルンは、わけのわからない数列が∑とともに ∫ に変身する様に半分うんざりしながらも「これって行列ちゃうか？」と気が付きました。

ハイゼンベルクはアイディアばつぐんの天才肌青年でしたが、最新の数学には通じていませんでした。

ボルンはというと、行列については多少知識がありました。

それで、この方面に強い教え子パスカル・ヨルダンを呼び寄せて、ハイゼンベルクの論文を行列で書き表してみせました。

ＰＱ－ＱＰ＝Ｉ

ＰとＱはそれぞれ行列です。Ｉは単位行列。こんな式が最終的に浮かび上がってきました。

同じ頃、ドイツではなくイギリスで、ポール・ディラックが違う閃きをもとに、これと酷似した数式に到達していました。

ｐｑ－ｑｐ＝ａ

ここにあるｐとｑは行列ではなく、代数的変数です。ａは私がてきとーに選びました。ディラックがひねり出した式は本当は「ａ」のところに虚数「ⅰ」とかプランク定数「ｈ」とか円周率「π」とかが一塊で出てきますが、ここでは「ＰＱ－ＱＰ＝Ｉ」との形式的類似について話を絞りたいので「ｐｑ－ｑｐ＝ａ」としました。

ハイゼンベルク一派は行列を使いましたが、ディラックはというと、この式を見出した後、ここに何か新しい代数が潜んでいると直観しました。

２×３は３×２と同じ値になるけれど、これとは違って ①変数の前後を入れ替えると積が同じにならない、②入れ替えたものどうしを引き算すると一定の値になる、そういう代数を新たに作ってまえ！と考えました。（ここでは「ｑ代数」と呼んでおきます）

ハイゼンベルク一派は「行列」を、孤高ディラックは「ｑ代数」を拠り所に、電子の軌道について前代未聞の研究に乗り出したわけです。

ここでもうひとつ、つまり三つ目の代数が登場します。登場というか、行列よりもっと使い勝手のいい代数があったらいいなと、ハイゼンの師匠ボルンは考えました。

そこでアメリカのマサチューセツ工科大学（いわゆるＭＩＴ）に招かれた際に、彼はそこのど天才数学者ノーバート・ウィーナーに自分のアイディアを伝え、このテーマで共同研究しました。

ウィーナーはかつて12歳にして大学生になったぐらいの頭脳で、その後確率論の研究を進めてブラウン運動の確率論的解釈など、物理学のいろいろな現象をウィーナー過程と後に呼ばれることになる考え方で語り、ドイツのゲッチンゲン大（当時の欧米で数学と物理学の最高知性が集ったところ）の俊才たちからも一目置かれていた方です。

彼は前にゲッチンゲンに来て講義を行ったことがあって、ボルンとも面識がありました。そして彼のアイディアをたちどころに理解して、ふたりで議論を続け、そして「演算子」の考え方を使えば「行列」よりもスマートにくだんの電子軌道の謎を語れることに彼らは気づきました。

その論文を紹介します。「Journal of mathematics and physics」（数理物理ジャーナル）1926年1月発行ぶんに掲載されたものです。

タイトルは「周期的および非周期的現象の量子化法則の新しい定式法」といいます。

全１５頁。かいつまんで内容を説明すると、原子における電子は、原子核を電子がぐるぐるまわるイメージで語れるけれど、それとは別に「自由電子」と呼ばれる電子があって、これはぐるぐるまわっていないため、行列メソッドでは取り扱えないわけです。

そういう自由な電子についても語れるような数学が要ると考え、ボルンとウィーナーのふたりでそれを探求いたすと、そういう前説でスタートです。

順に目を通していくと…

出てきました「ｐｑ－ｑｐ＝ａ」の式が。

しかしよく読むと、これらｐとｑについてボルン＆ウィーナーは「operator」と呼んでいます。行列でも代数でもなく「演算子」であると。

演算子ってなんだべ？という方のために説明すると…

関数は分かりますね？ 関数を微分したり積分したり、ほかいろいろ演算する過程を一くくりに「演算子」と呼んでいます。これはライプニッツが微積の記号 d とか ∫ とかの記号を作ったのが始まりです。１９世紀末に、イギリスのオリヴァー・ヘヴィサイドが電磁気学に応用して実用的なものとして重宝されました。２０世紀になると電気工学の方面でいろいろ応用されました。

ウィーナーも電気畑の方だったで演算子を使ったフーリエ変換の手法を編み出したりと、もともと縁のある考え方でした。

それを電子の軌道（軌跡というべきでしょうか）の数式による記述に使えるんやないか…ボルンとそこまで考えを進めたのです。

周期的でない電子、つまり自由電子についても、原子核に付随する電子と同じ演算子を使って記述できることを、ふたりはこの論文で示してみせました。ボルンのアイディアは、ウィーナーのおかげで一応達成されたわけです。

いちおうです。

実はこの二人、あることを見過ごしてしまったのです。ここです。

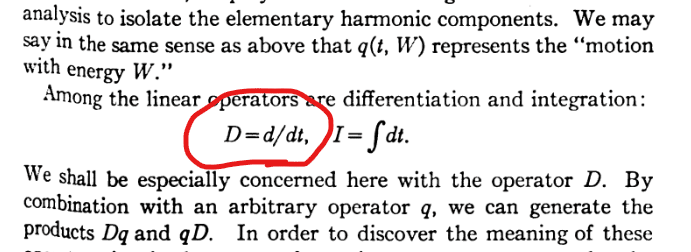
赤で括ったのは微分演算子ですね「d / dt」。これを演算子「Ｄ」と名付けて「W」（エネルギー）に作用させるところまでは二人とも実行したのですが…

「ｄ/ ｄｑ」という微分演算子には考えが至らなかったのです。

もし考えていたら、この微分演算子を運動量ｐに作用させる、すなわち座標ｑにおける運動量ｐを表す演算子が作れるぞって。

もしこのことに気づいていたら…

この五か月後、‎エルヴィン・シュレディンガーが、後に「シュレディンガー方程式」と呼ばれることになる画期的方程式を提唱した論文が出ました。

後日じっくり検証するつもりですが、この論文の中でシュは、電子の運動エネルギーが運動量の二乗と関係することを指摘しています。シュ方程式の肝ですね肝。

ボルンとウィーナーのふたりが、もし「ｄ/ ｄｑ」という微分演算子についても思索を深めていたら、これを使って「ｄｐ/ｄｑ」すなわち運動量ｐに対応する演算子であること、そしてエネルギー演算子との絡みがいいことに気づいて、シュ方程式にあたるものをねん出していたのではないか…と思うのです。

これは私の勝手な想像ではありません。ボルンそのひとが後に「ちくしょうあそこでもそっと粘ってたら…」と発言を残していることからもわかるように、もし粘っていたらウィーナーの頭脳に支えられて彼はそこまで到達できていたと考えます。

その後、その口惜しさを挽回するかのように、違う画期的アイディアを彼は同1926年後半に提唱して、これが後にノーベル物理学賞に輝くことになります。その受賞記念講演（1959年）でも「ちっくしょーウィーナーとあそこでもそっと粘ってたら…しかしシュレディンガーの功績は認めざるをえないね」と謙虚に振り返っています。