「ああ、あれってこれのことやったんか！」と伏線回収される心地よさと、明日への希望が予告編されるのが、高校数学の「数Ⅲ」つまり理系用微積コースだといわれます。小学校の５年生あたりで円の面積について習いませんでしたか。こんなの。

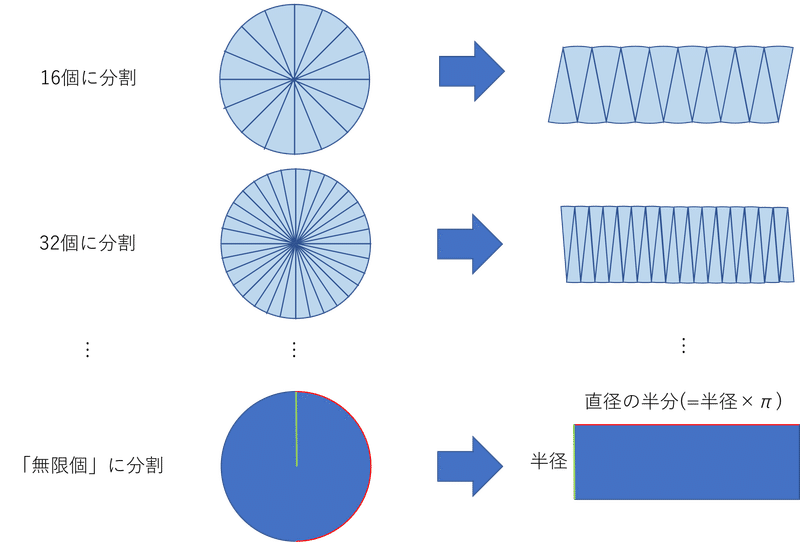
今は小６で習うのですが私はもっと早くに習いました。ひとりで先に学びました。何しろ見ればわかるから。小学校の図書室には、各学年向けの学習誌がひとつの棚に置かれていて、その気になれば小４の子が小６向けのものを閲覧しても別に構わないわけです。だから同学年の子たちより先にいろいろひとりで学んでしまう（少なくとも知る）のは、自分にとってはそんなに不思議なことではありませんでした。

その後、数Ⅲ（一部の上位校を除けば高校３年で習う）で、円の面積の算出法を改めて習います。もっと難しめにですが、考え方は同じです。無限小幅のスライスを足し算していくの。

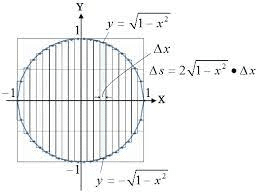
これを習って感動した方は少なくないと思います。「おお小６で習ったあれのもっとかっこいい、おとなバージョンやんか！」と。さらにこの後、微分方程式のイロハを習い、多少耳年増さんなら、微分方程式を使うと野兎の増加と安定が予想できるとかの類の応用法を目にして「よっしゃあ大学進んだらばりばりこれ勉強したるねん！」と理系ダマシイを膨らませたりしてね。性差のことはこの際無視。こういう伏線回収の快感と明日への希望をひとり味わいつつ、受験勉強にいそしむのが受験数学秀才くんたちの半ばパターンです。

ところが進学後、数学の講義を受けていくにつれて、だんだんわけわかんなくなっていくわけですよ。積分にもいろいろあると知って、ああそうなのかとわくわくするなか、やがてリーマン積分とかルベーグ積分とか、変なのを語られて、次第に自分が今どこあたりにいるのかわからなくなっていきます。測度空間がどうのリースの定理がこうの、もっと先には積分方程式を通してクラメールの解法が無限次元では固有値０の場合どうたらこうたら作用素が不連続でヒルベルト空間がバナッハしてああだこうだと濁流に呑み込まれてほうほうのていで単位は取って卒業証書をなんとか頂戴する…学部や専攻によってどこまで何を習うかは違うとして、この感覚はわかるひとにはわかると考えます。

どうして受験数学秀才さんたちが落ちこぼれていくのかというと、私見ですが小１より体で叩きこまれたものを大学で脱臭しないまま、絶壁上りを続けてとうとう延長ロープが伸びきってそこより上に行けなくなってしまうのです。小１のさんすうのじゅぎょう、思い出してください。

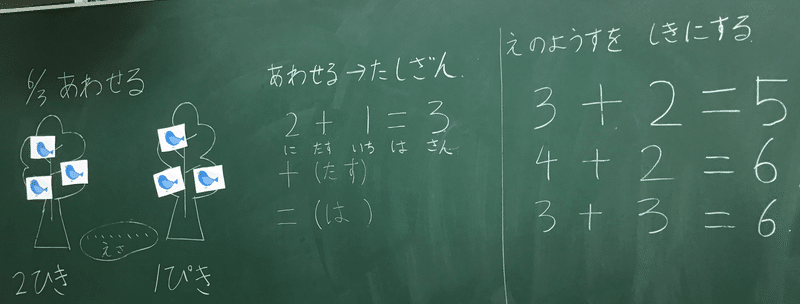
これはかなり意欲的な教え方をされていますね。いずれにせよ基本は「数える」です。数えることがさんすうのきほんだと、私たちは小１より叩きこまれます。

ところが大学で習う数学は、数えるが数学の基本でも基礎石でもない世界です。「１＋１＝２であることを証明しろ」みたいな問いを真正面からぶつけられます。これを証明せよというからには、１＋１＝２は絶対的なものではなく、もっと絶対的なものが他に仮定されているわけです。それを受け入れられるかな、と。

１９世紀後半、ヨーロッパの最高の数学知性が命をかけて激突した大バトルでもありますこれは。その後、精神病院で亡くなった方までいます。皮肉なことに亡くなったこの方による「数えることは数学の絶対根拠ではない」スタンスこそが今では正統となって久しいです。

私は勇気を振り絞って、独りで行けるところまで行ってみることにしました。そして「集合と写像」という、現代数学の絶対的根拠にまでたどり着きました。（圏論は？というツッコミは今は控えてください数学徒の皆さま）　ブルバキの皆さまが作り上げた、現代数学の一大スーパーハイウェイ。そのセントラルステーション、ハブエアポートが「集合と写像」。その地点より小１から大学入試までの学校数学を眺めなおすと…

 すごく政治の力を感じます。国家の意思というべきかな。歴代のさんすう、数学の教科書を眺めていっても、その時代その時代の優先事項、焦り、不安などが色濃くうかがえます。

別に自分を目覚めし者と考えるとか恍惚と不安を感じるとかはないのですが、それに近いものをちらっとは感じないでもない気がする一瞬がごくたまにあるとはけして言わないでおこうと、そんなことを駄文の体裁でそっとつぶやいておくのも青春の１ページになるかもしれないわね鉄郎。