円
途中ですしChatGPTですしミスも誤解もありますし。
参考
途中でぶっこんでるオイラー法
テイラー展開
ただしまだ十分でない。
ベクトル解析のページでも触れた気がする。
連立方程式をとくだのとかないだのとけないだのはこちらへん。
円の定義
円とは、中心から一定距離にあるすべての点の集まりです。
数学的には、中心が$${ (h, k) }$$で半径が$${r}$$の円の方程式は次のように表されます。
$$
(x - h)^2 + (y - k)^2 = r^2
$$
中心が$${(0, 0)}$$なら$${x^2+y^2=r^2}$$です。
円周は $${ 2\pi r }$$です。
円の面積は $${ \pi r^2 }$$ です。
一般形
$$
x^2 + y^2 + Dx + Ey + F = 0
$$
パラメトリック形式
角度パラメータ $${ t }$$ を使って
$$
x = h + r\cos t\\
y = k + r\sin t
$$
と表すことができます。
中心が$${(0, 0)}$$なら
$$
x = r\cos t\\
y = r\sin t
$$
です。
パラメトリック形式は$${f(t)}$$であって、出力はベクトルです。
陽関数形式
陽関数形式では、関数が $${ y }$$ を $${ x }$$ の関数として明示的に解かれています。上述した円の方程式を $${ y }$$ について解くと、次の2つの解が得られます。
$$
y = k \pm \sqrt{r^2 - (x - h)^2}
$$
この式は、$${ x }$$ の各値に対して2つの $${ y }$$ の値(上半円と下半円)を提供します。陽関数形式は、特定の $${ x }$$ 値に対する $${ y }$$ の値を直接計算する場合に便利ですが、$${ x }$$ の範囲が $${ h-r }$$ から $${ h+r }$$ までと限定され、$${ r^2 - (x - h)^2 }$$ が非負である必要があります。
中心が$${(0, 0)}$$の場合
$$
y = \sqrt{r^2 - x^2}
$$
陰関数形式
陰関数形式では、関数が $${ y }$$ を明示的に解かない形で表されます。円の最も一般的な陰関数形式は、中心が $${ (h, k) }$$で半径 $${ r }$$ の円の場合、次のように表されます。
$$
(x - h)^2 + (y - k)^2 = r^2
$$
この形式では、$${ x }$$ と $${ y }$$ が等式で結ばれていますが、$${ y }$$ について解くことはされていません。これが「陰関数」の特徴です。
中心が$${(0, 0)}$$の場合
$$
x^2 + y^2 = r^2
$$
あるいは
$$
x^2 + y^2 - r^2= 0
$$
陰関数は$${f(x, y)}$$で表すと
$$
f(x, y) = x^2 + y^2 - r^2= 0
$$
です。
つまり出力常にゼロです。
$${ f(x, y) = x^2 + y^2 - r^2 }$$において
$${ f(x, y) = 0 }$$ を満たす点 $${ (x, y) }$$ は、半径$${ r }$$の円上にあります。
$${ f(x, y) > 0 }$$ の場合、点 $${ (x, y) }$$ は円の外側にあります。
$${ f(x, y) < 0 }$$ の場合、点 $${ (x, y) }$$ は円の内側にあります。
出力がゼロでなく、
$$
f(x, y) = x^2 + y^2 + z^2= r^2
$$
の場合は球面です。
$$
f(x, y) = x^2 + y^2= z^2
$$
の場合は円錐です。
放物面
円形放物面
放物面の一種で、軸が垂直な円錐の断面である放物線によって生成されます。
$$
z = \frac{x^2 + y^2}{4p}
$$
ここで、$${ p }$$ は焦点までの距離(焦点パラメータ)を表し、$${ x,y,z }$$ はそれぞれ座標軸です。この形式では、すべての点が$${ z }$$ 軸に関して対称で、放物面は上向きです。
楕円放物面
$$
z = \frac{x^2}{a^2} + \frac{y^2}{b^2}
$$
ここで、$${ a }$$ と $${ b }$$ はそれぞれ $${ x }$$ 軸と $${ y }$$ 軸に沿った楕円の半径を表します。この場合、放物面は $${ z }$$ 軸に関して対称であり、放物面の断面は楕円です。
双曲放物面
サドル形状の放物面
$$
z = \frac{x^2}{a^2} - \frac{y^2}{b^2}
$$
この方程式は双曲放物面を表し、$${ x }$$ 方向と $${ y }$$ 方向で曲率が異なるサドルのような形状をしています。$${ a }$$ と $${ b }$$ は放物面の幅を調整します。
微分と勾配
パラメトリックな円の方程式$${\bm r(t)=(r\cos t, r \sin t)}$$は入力が1変数、出力がベクトル(2値)でありベクトル値関数です。また、位置ベクトルを意味します。パラメータが1つなので微分可能な場合があり、円の場合は可能です。微分すると速度ベクトル$${\bm v(t)=(-r\sin t, r \cos t)}$$となり、これは円の接線方向を向きます。
円の場合、ある意味で特殊な結果として、$${\bm r(t)\cdot \bm r'(t)=\bm r(t)\cdot \bm v(t)=0}$$です。これは微分前のベクトルが全ての$${t}$$において同じ大きさの場合に起こります。つまり円とか球です。それ以外ではなかなか起こりません。
陰関数形式の円の式は$${f(x,y)=x^2+y^2-r^2}$$の入力2変数、出力スカラーのスカラー値関数と見做し、その微分操作に相当する勾配$${f(x,y)=(2x, 2y)}$$は円の法線方向を向きます。
数学における関数の微分について、異なる種類の関数の微分法を簡潔にまとめます。具体的には、1変数のスカラー値関数、1変数のベクトル値関数、多変数のスカラー値関数、および多変数のベクトル値関数の微分について説明します。
1変数入力のスカラー値関数の微分
定義と例:
関数 $${ f(x) }$$ がスカラー値であり、$${ x }$$ が一つの実数変数である場合、この関数の微分 $${ f'(x) }$$ は、$${ x }$$ の小さな変化に対する $${ f(x) }$$ の変化の割合を示します。
例:$${ f(x) = x^2 }$$ の微分は $${ f'(x) = 2x }$$。
$$
y = \sqrt{r^2 - x^2}
$$
の場合、
一般的な関数 $${ f(x) = x^n }$$ の微分は$${f'(x) = nx^{n-1}}$$であって
$${\sqrt{x}}$$は$${x^{\frac{1}{2}}}$$かつ$${x^{-1}}$$は$${\frac{1}{x}}$$であるから、$${\frac{d}{dx} \sqrt{x}=\frac{1}{2\sqrt{x}}}$$
微分の連鎖律(合成関数の微分)として
関数 $${ y = f(u) }$$ があるとき、もしもう一つの関数 $${ u = g(x) }$$ が存在するならば、合成関数 $${ y = f(g(x)) }$$ の $${ x }$$ に対する微分は次のように計算されます:
$$
\frac{dy}{dx} = \frac{df}{du} \cdot \frac{du}{dx}
$$
なので
$$
f(x)=\sqrt{g(x)}\\
g(x)=r^2 - x^2\\
f'(x)=\frac{1}{2\sqrt{g(x)}}\\
g'(x)=-2x
$$
とするなら
$$
y = \sqrt{r^2 - x^2}
$$
の微分は
$$
f'(x) = \frac{d}{dx} \sqrt{g(x)} = \frac{1}{2\sqrt{g(x)}} \cdot g'(x)
$$
$$
\frac{d}{dx} \sqrt{r^2 - x^2} = \frac{1}{2\sqrt{r^2 - x^2}} \cdot (-2x) = -\frac{x}{\sqrt{r^2 - x^2}}
$$
つまり
$$
-\frac{x}{\sqrt{r^2 - x^2}}=-\frac{x}{y}
$$
これは接線の傾きです。
曲線上の微小領域におけるxとyの比です。
これをGoogle Colab上で評価してみましょう。
ただしr=1, x=0から1まで0.1刻み。
import numpy as np
# 定義された範囲と刻み幅でxの値を生成
x_values = np.arange(0, 1.1, 0.1)
# rの値
r = 1
# 式を評価
# ここでx = rの場合、分母が0になるため、定義域外の値は除外
results = [-x / np.sqrt(r**2 - x**2) if x != r else None for x in x_values]
# 結果の出力
for x, result in zip(x_values, results):
print(f"x = {x:.1f}, f(x) = {result}")x = 0.0, f(x) = -0.0
x = 0.1, f(x) = -0.10050378152592121
x = 0.2, f(x) = -0.20412414523193154
x = 0.3, f(x) = -0.31448545101657555
x = 0.4, f(x) = -0.4364357804719848
x = 0.5, f(x) = -0.5773502691896258
x = 0.6, f(x) = -0.7500000000000002
x = 0.7, f(x) = -0.980196058819607
x = 0.8, f(x) = -1.3333333333333337
x = 0.9, f(x) = -2.0647416048350564
x = 1.0, f(x) = None
x = 1 付近でyが急激に変動し、一生懸命曲がろうとしているのがわかります。xが定点なので、yの方で増加しなければ帳尻が取れないわけです。
オイラー法で再現してみましょう。オイラー法なので、せっかく微分したものを近似積分して元に戻してることになります。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r = 1 # 半径
x = np.arange(0, r + 0.1, 0.1) # 0から1まで0.1刻み
# 微分式を利用して y の値を数値的に求める
y = np.zeros_like(x)
y[0] = r # x=0 の時の y の初期値は r
# 微分式 dy/dx = -x / sqrt(r^2 - x^2) を用いて、オイラー法で y を更新
for i in range(1, len(x)):
dx = x[i] - x[i - 1]
dy_dx = -x[i - 1] / np.sqrt(r**2 - x[i - 1]**2)
y[i] = y[i - 1] + dy_dx * dx
# プロット
plt.figure(figsize=(6, 6))
plt.plot(x, y, label='Upper half-circle calculated using differential equation')
plt.scatter(x, y, color='red') # 座標点を赤でマーク
plt.xlabel('x')
plt.ylabel('y')
plt.title('Upper Half-Circle Calculated Numerically')
plt.legend()
plt.grid(True)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.show()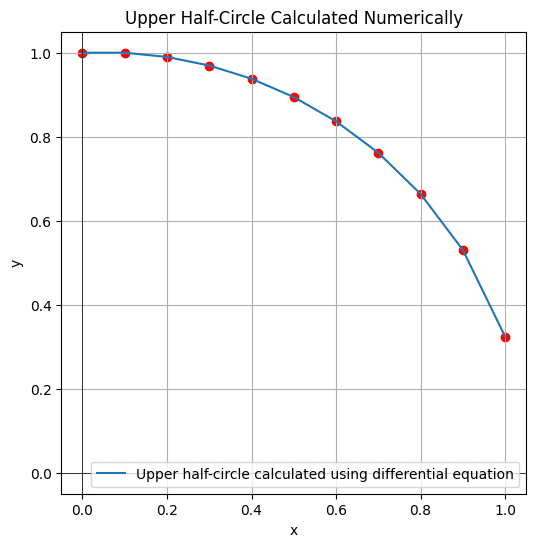
1変数入力のベクトル値関数の微分
定義と例:
関数 $${ \mathbf{r}(t) }$$ がベクトル値であり、入力 $${ t }$$ が一つの実数変数である場合、この関数の微分 $${ \mathbf{r}'(t) }$$ は、$${ t }$$ の小さな変化に対する $${ \mathbf{r}(t) }$$ のベクトルの変化を示します。
例:$${ \mathbf{r}(t) = (t^2, t^3) }$$ の微分は $${ \mathbf{r}'(t) = (2t, 3t^2) }$$。
また
$$
\mathbf{r}(t)=(x(t),y(t))
$$
ならば、その微分
$$
\mathbf{r}'(t)=(x'(t),y'(t))
$$
は接線ベクトルである。
例えば
$$
x = r\cos t\\
y = r\sin t
$$
ならば、三角関数の微分は
$$
\frac{d}{dx} \sin x = \cos x\\
\frac{d}{dx} \cos x = -\sin x
$$
であるから
$$
\frac{dx}{dt} = -r\sin t\\
\frac{dy}{dt} = r\cos t
$$
これは接線ベクトルである。
陽関数のように$${y}$$が$${x}$$に依存してないため、
単純にベクトル$${(dx, dy)}$$を曲線の進行方向と見ることができる。
多変数入力のスカラー値関数の微分
定義と例:
関数 $${ f(x, y) }$$ がスカラー値で、入力が複数の実数変数 $${ x, y }$$ である場合、この関数の勾配 $${ \nabla f(x, y) }$$ は、各方向の偏微分をベクトルとして組み合わせたものです。
例:$${ f(x, y) = x^2 + y^2 }$$ の勾配は $${ \nabla f(x, y) = (2x, 2y) }$$。
$$
x^2 + y^2 = r^2
$$
の場合、やはり勾配は
$$
\nabla f(x, y) = (2x, 2y)
$$
であって、このベクトルは原点から円の外に放射する。
ちゃんとした勾配はマイナスがつくので原点に向かう。
import numpy as np
# パラメータ設定
r = 1 # 半径
x = np.arange(0, r + 0.1, 0.1) # 0から1まで0.1刻み
# yの値を計算
y = np.sqrt(r**2 - x**2)
# 各(x, y)点における勾配ベクトルを計算
gradient_vectors = [(xi, yi, 2 * xi, 2 * yi) for xi, yi in zip(x, y)]
# 勾配ベクトルの結果を出力
gradient_vectors
$$
x = 0.0, y = 1.0, \nabla f = (0.0, 2.0) \\
x = 0.1, y = 0.995, \nabla f = (0.2, 1.990) \\
x = 0.2, y = 0.980, \nabla f = (0.4, 1.960) \\
x = 0.3, y = 0.954, \nabla f = (0.6, 1.908) \\
x = 0.4, y = 0.917, \nabla f = (0.8, 1.833) \\
x = 0.5, y = 0.866, \nabla f = (1.0, 1.732) \\
x = 0.6, y = 0.800, \nabla f = (1.2, 1.600) \\
x = 0.7, y = 0.714, \nabla f = (1.4, 1.428) \\
x = 0.8, y = 0.600, \nabla f = (1.6, 1.200) \\
x = 0.9, y = 0.436, \nabla f = (1.8, 0.872) \\
x = 1.0, y = 0.0, \nabla f = (2.0, 0.0)
$$
よく見るまでもなく2倍しとるだけである。
とりわけ原点を中心とした円は、座標ベクトルがそのまま勾配の逆方向であって、座標ベクトルを逆にしたら勾配方向である。
多変数入力のベクトル値関数の微分
定義と例:
関数 $${ \mathbf{F}(x, y, z) }$$ がベクトル値で、入力が複数の実数変数である場合、この関数のヤコビアン $${ J_{\mathbf{F}} }$$ は、各成分の勾配を行として持つ行列です。
例:$${ \mathbf{F}(x, y, z) = (xy, yz, zx) }$$ のヤコビアンは
$$
J_{\mathbf{F}}(x, y, z) =
\begin{bmatrix}
y & x & 0 \\
0 & z & y \\
z & 0 & x
\end{bmatrix}
$$
これらの微分法はそれぞれの関数の種類に応じて異なり、関数の性質や応用によって異なる数学的手法を要求します。スカラー値関数は個別の変化率や方向微分(勾配)を提供し、ベクトル値関数はそれが複数の次元にわたって展開されます。これらの基礎は、高度な数学や物理学、工学の問題を
3点通る円および曲率半径
三点を通る円の半径(曲率半径)を求めるためには、まずはそれら三点を通る円の方程式を設定し、それから半径を求める計算を行います。ここで、三点 $${ (x_1, y_1) , (x_2, y_2) , (x_3, y_3) }$$ が与えられたとします。これらの点を通る円の半径 $${ R }$$ を求める一般的な公式は以下のように導出されます。
步み
三点から二つの中点を求めます:
点 $${ A }$$ と $${ B }$$ の中点: $${ M = \left( \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2} \right) }$$
点 $${ B }$$ と $${ C }$$ の中点: $${ N = \left( \frac{x_2+x_3}{2}, \frac{y_2+y_3}{2} \right) }$$
中線の方程式を求めます:
点 $${ A }$$ と $${ B }$$ を結ぶ線の傾き $${ m_{AB} = \frac{y_2 - y_1}{x_2 - x_1} }$$
点 $${ B }$$ と $${ C }$$ を結ぶ線の傾き $${ m_{BC} = \frac{y_3 - y_2}{x_3 - x_2} }$$
それぞれの中線の傾き(垂直二等分線)を求める:
$${ m_{AB} }$$ の垂直二等分線の傾き $${ m_{\perp AB} = -\frac{1}{m_{AB}} }$$
$${ m_{BC} }$$ の垂直二等分線の傾き $${ m_{\perp BC} = -\frac{1}{m_{BC}} }$$
垂直二等分線の方程式を設定し、その交点を求める:
これは、円の中心を求める計算になります。
方程式を解くことで円の中心 $${ (x_c, y_c) }$$ を求めます。
円の半径を計算:
任意の点 $${ (x_1, y_1) }$$ から中心 $${ (x_c, y_c) }$$ までの距離が半径 $${ R }$$ です。
$${ R = \sqrt{(x_c - x_1)^2 + (y_c - y_1)^2} }$$
具体的な計算
実際の計算では行列や連立方程式を用いることが一般的で、半径Rを求めるために次のような公式を使います:
$$
R = \frac{a \times b \times c}{4 \times \text{Area of triangle ABC}}
$$
ここで、$${ a, b, c }$$ は三辺の長さ、Area of triangle ABC は三点による三角形の面積です。面積はヘロンの公式や行列式を用いて求めることができます。この方法は、三角形の各辺の長さと面積を用いて、直接的に半径を求めるアプローチです。
import numpy as np
def calculate_circle_radius(x1, y1, x2, y2, x3, y3):
# 3点の座標を配列として定義
points = np.array([[x1, y1], [x2, y2], [x3, y3]])
# 各辺の長さを計算
a = np.linalg.norm(points[0] - points[1])
b = np.linalg.norm(points[1] - points[2])
c = np.linalg.norm(points[2] - points[0])
# 三角形の面積を求める(ヘロンの公式)
s = (a + b + c) / 2
area = np.sqrt(s * (s - a) * (s - b) * (s - c))
# 三点を通る円の半径を計算
if area == 0:
return None # 三点が一直線上にある場合、半径は定義できない
radius = (a * b * c) / (4 * area)
return radius
# 例: 三点の座標を指定
x1, y1 = 0, 0
x2, y2 = 1, 0
x3, y3 = 0.5, np.sqrt(3)/2
# 半径を計算して表示
radius = calculate_circle_radius(x1, y1, x2, y2, x3, y3)
print(f"The radius of the circle passing through the given points is: {radius}")
この計算では、三点が一直線上にある場合(面積がゼロの場合)には、半径を計算することができない点に注意してください。
連立方程式から円の中心点
未テスト
import numpy as np
def calculate_circle_center(x1, y1, x2, y2, x3, y3):
# 二点間の中点を求める関数
def midpoint(x1, y1, x2, y2):
return (x1 + x2) / 2, (y1 + y2) / 2
# 中点を求める
mx1, my1 = midpoint(x1, y1, x2, y2)
mx2, my2 = midpoint(x2, y2, x3, y3)
# 中線の傾きが0でない場合、その逆数を取る。0なら無限大(垂直)とする。
def slope(x1, y1, x2, y2):
if x2 - x1 != 0:
return (y2 - y1) / (x2 - x1)
else:
return None
# 傾きを計算
slope1 = slope(x1, y1, x2, y2)
slope2 = slope(x2, y2, x3, y3)
# 垂直二等分線の傾き(傾きが存在する場合、逆数の符号を反転)
if slope1 is not None:
perp_slope1 = -1 / slope1
else:
perp_slope1 = 0
if slope2 is not None:
perp_slope2 = -1 / slope2
else:
perp_slope2 = 0
# 垂直二等分線の方程式を行列で解く
A = np.array([
[-perp_slope1, 1],
[-perp_slope2, 1]
])
b = np.array([
-perp_slope1 * mx1 + my1,
-perp_slope2 * mx2 + my2
])
# 連立方程式を解く
center_x, center_y = np.linalg.solve(A, b)
return center_x, center_y
# 三点の座標
x1, y1 = 0, 0
x2, y2 = 4, 0
x3, y3 = 2, 4
# 円の中心を計算
center_x, center_y = calculate_circle_center(x1, y1, x2, y2, x3, y3)
print(f"The center of the circle passing through the given points is: ({center_x}, {center_y})")
このコードは、三点が一直線上にない場合に有効です。一直線上にある場合、連立方程式は解けない(または特異行列となる)ため、その場合はエラーが発生することを考慮する必要があります。
この記事が気に入ったらサポートをしてみませんか?
