子供のころ算数が好きだった。中でも図形が好きで、印象に残っている問題の1つに60°20°50°30°の角度の問題がある。もしかしたら数学を好きになったきっかけかもしれない。記憶の扉が開いてこの問題を思い出した。本当に求まるの？って思いながら補助線引いてあれこれ考えるのが楽しかった。

具体的には次の図の？の角度を求める問題だ。解く過程で何度か「気づく」気持ちよさがあり、答えがきれいな数字になるし、改めて解答を見てもやられた感がある。

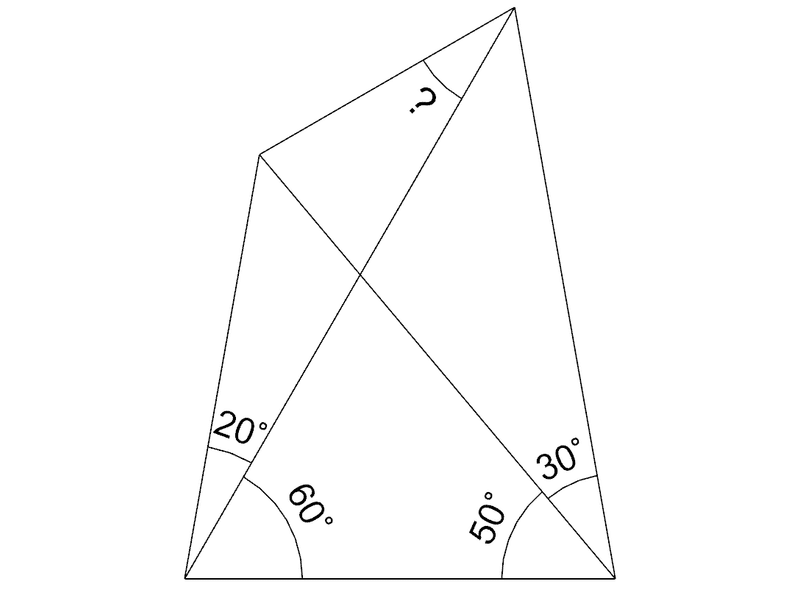
この記事を書くにあたり調べて初めて知ったが、ラングレーの問題というらしい。有名なのでネット検索するといろいろな興味深い解説や考察を見つけられるが、せっかくなので考え方を実況するように解説を書いてみたい。

まず、3角形の内角の和は180°なので、ここは50°だ。

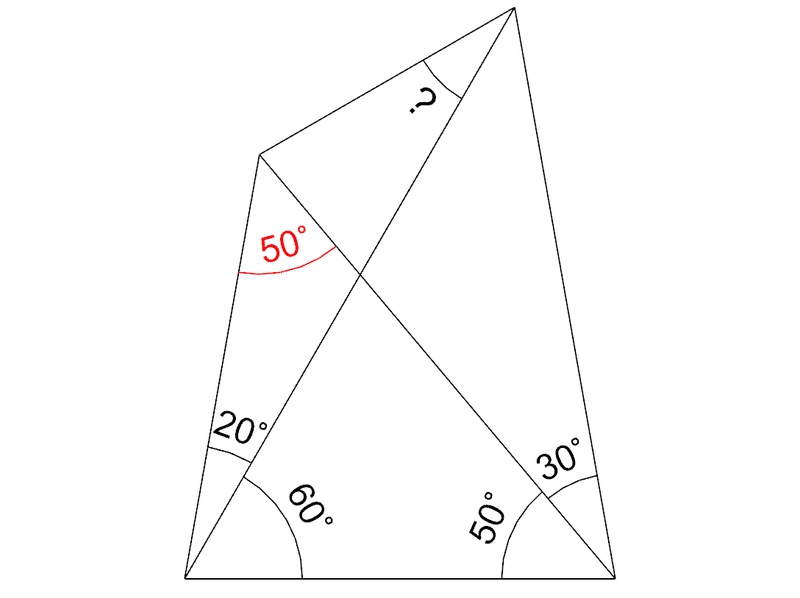
ということは、この3角形は2等辺3角形とわかる。

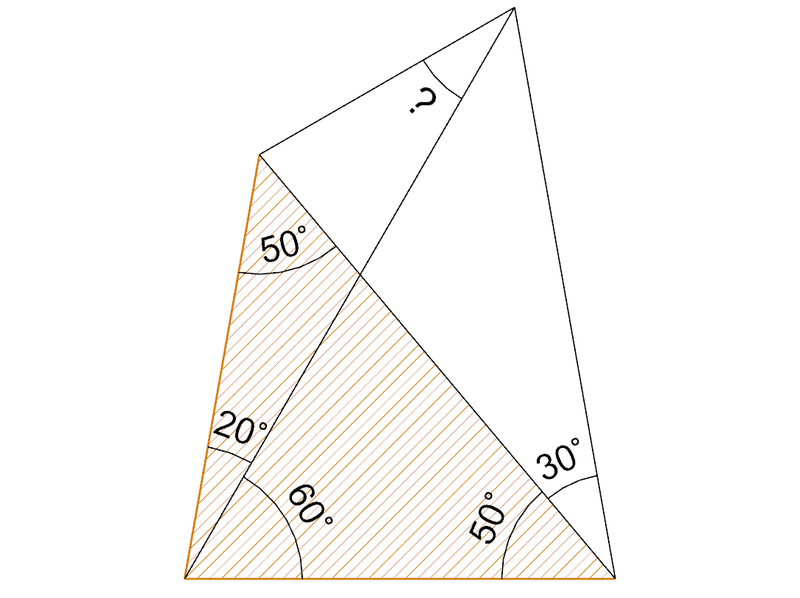
どこかに補助線を引くが、この2等辺3角形に関係するところに引くといいかもしれない。ということで、もう1つ同じ長さの辺を持つ2等辺3角形を作るように補助線を引いてみる。

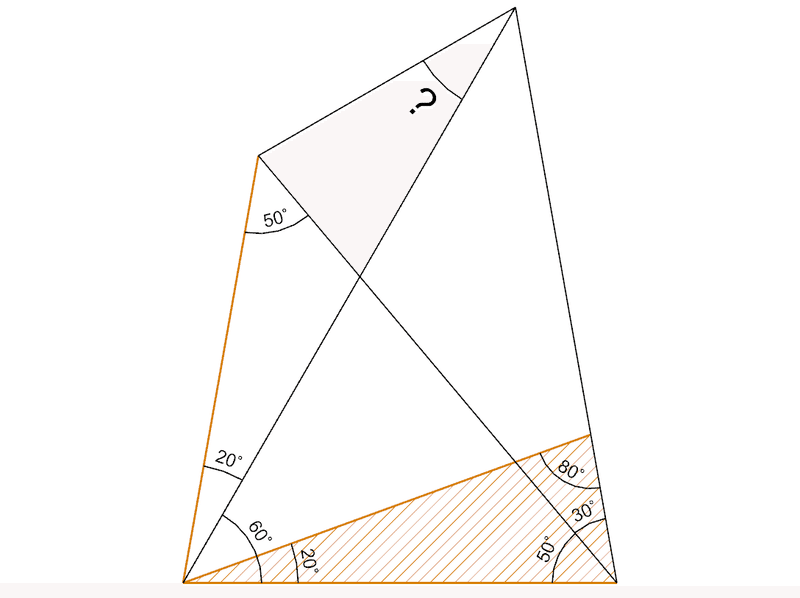
新たに現れた3角形の内角を計算すると、40°が2つ。

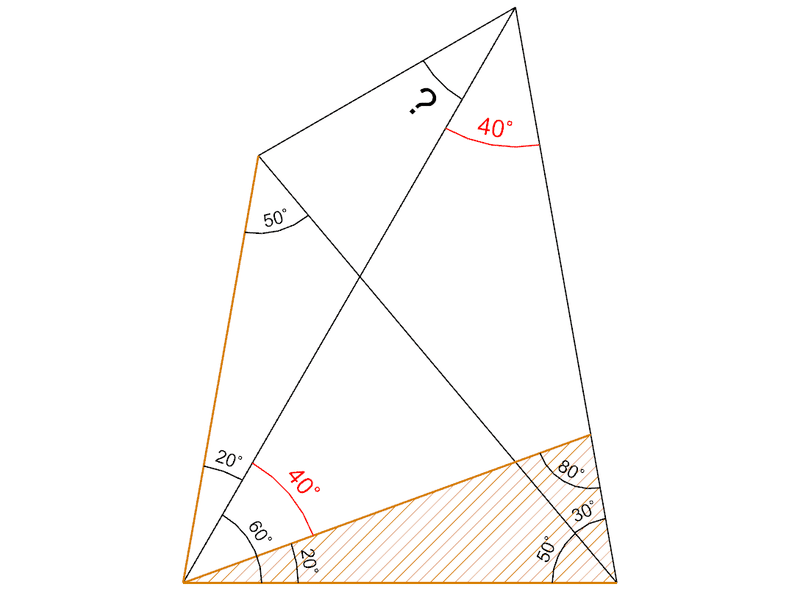
ということは、この3角形は2等辺3角形だ。

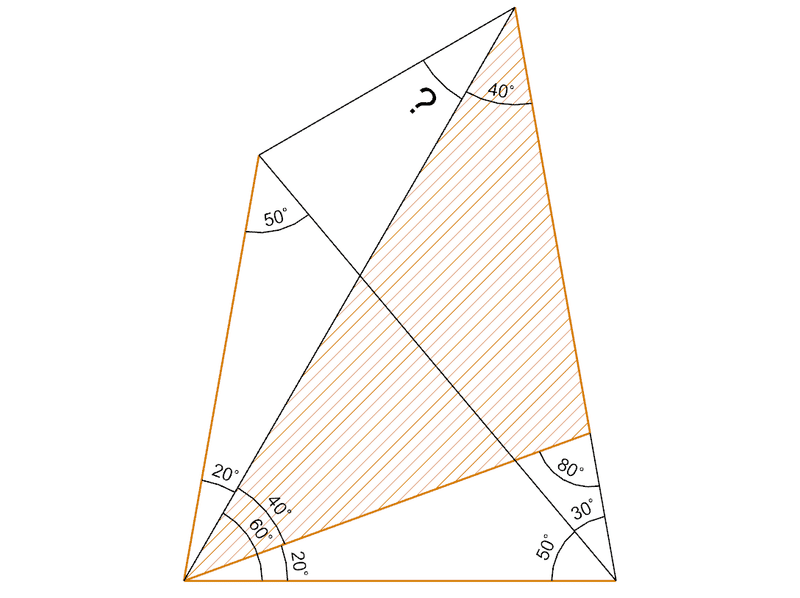
補助線を引くことで同じ長さの辺が4本になった。さて、この角度は60°で、両隣の辺の長さが同じということは…。

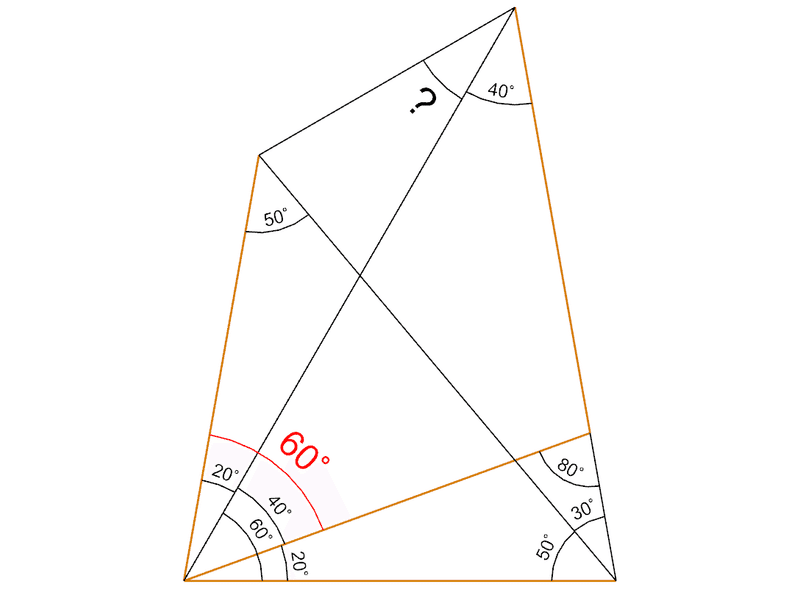
頂角が60°の2等辺3角形は正3角形なので、ここに正3角形ができている。
よって同じ長さの辺がさらにもう1本出てきた。

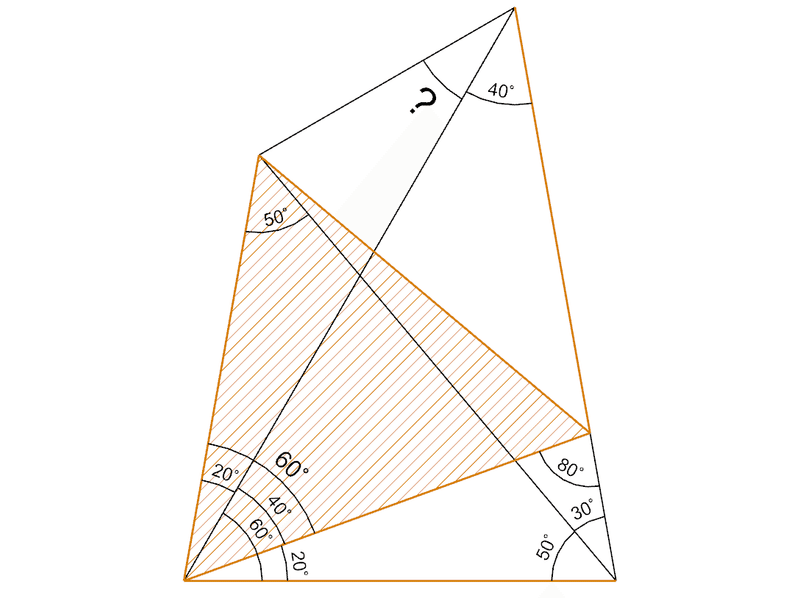
ということはこの3角形の2辺の長さが同じなので2等辺3角形ということがわかる。

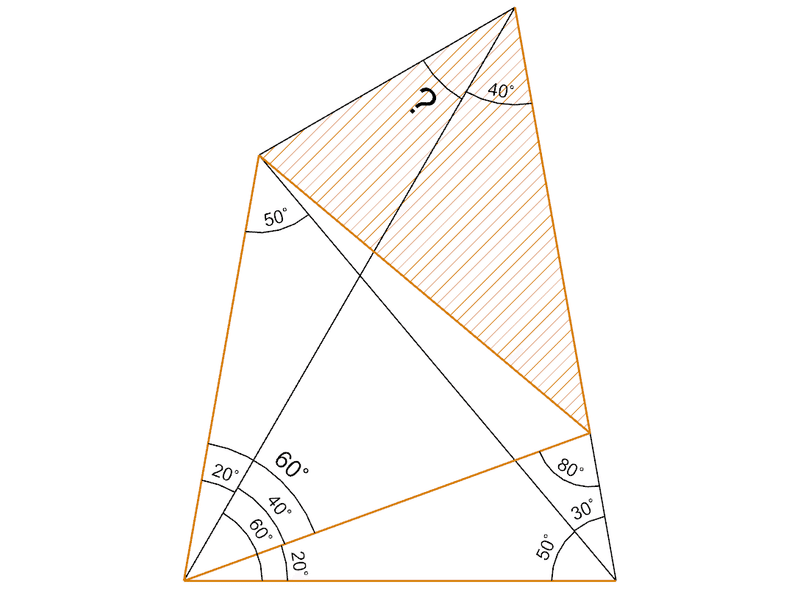
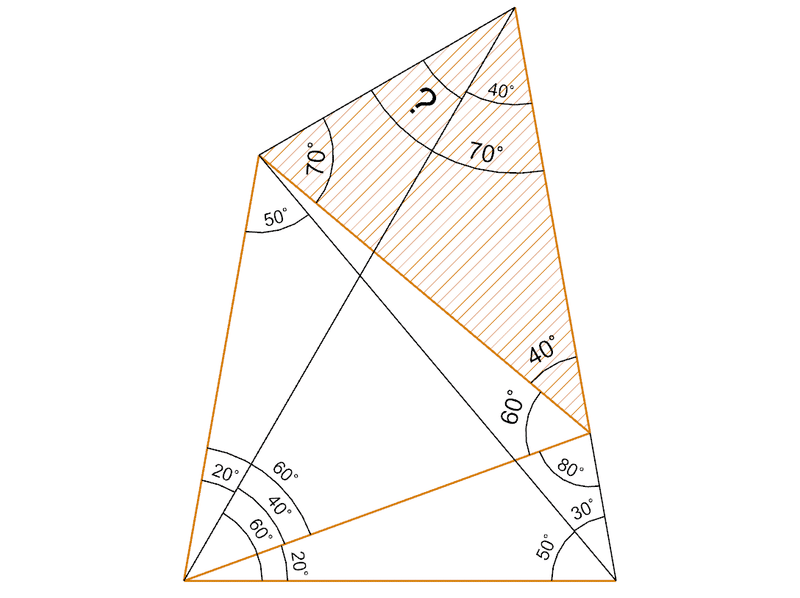
この2等辺3角形の内角を計算すると。

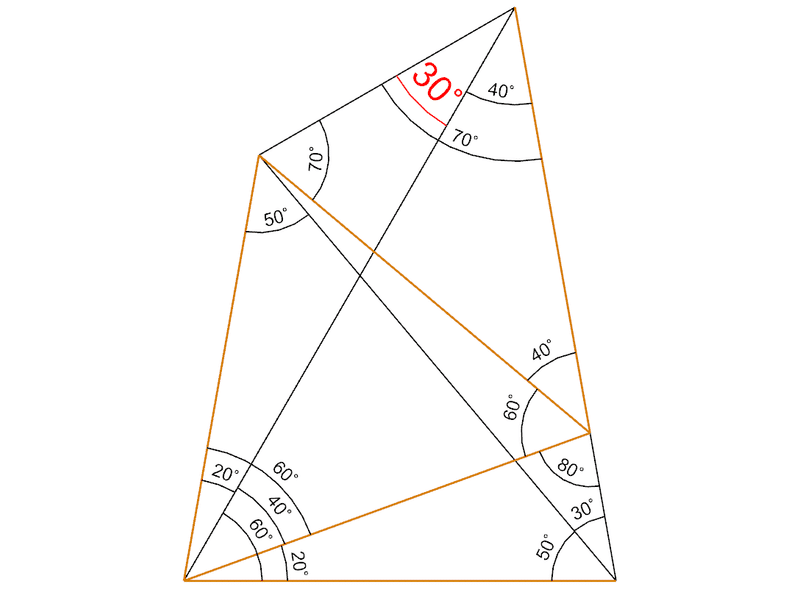
解けた！30°

なぜおもしろく感じるのかな？答えにたどり着くまでの手数や2等辺3角形が次から次に見つかる意外性ではないだろうか。「底角が同じだから2等辺3角形、よって辺の長さが等しい。」「辺の長さが同じだから2等辺3角形、よって底角が等しい。」という2通りの2等辺3角形の気づき方が両方含まれてるのもツボだろう。正3角形も絡んでいることでさらに美しい問題になっている。

書いていて子供のころに感じただろう感動を思い出せた。やはりこの問題は、数学を好きになったきっかけの1つだったかもしれない。

一件落着したところで、線で区切られたそれぞれの領域を冷蔵庫に貼るマグネットみたいにして遊んでみる。急にわけのわからない展開だが。

見つかった2等辺3角形たち。

ばらばらにして重ねる。

めくる。