「三角関数なんて生活のなんの役にも立たないっ！」って某元知事が吠えてたらしいですが、そんなことを言ったら、物理の知識なんてほとんど役にたたないです。

それはともかく、今朝、チーム員が面白いブログを紹介していました。「二次曲線の法則を知ると挫折に強くなる」というやつです。

出典：https://ameblo.jp/muni2525/entry-10990133747.html

ポイントは、練習（自転車に限らない）をしていてもなかなか成果が上がらないけど、あるときから急に成果が出てくる（ことがあるので）諦めないで、ということらしいです。

ただ、理系人間な人はこれ見たときに引っかかっると思うんですよね。まず、

二次曲線の法則

なんて聞いたことがない（笑　それで、ここの話は、別に「二次」である必要はまったくないのです。「一次」「二次」って何？と中学数学を忘れてしまった人向けにかくと、

ある量Aとある量Bが比例する　＝　一次

ある量Aの２乗 が　ある量Bと比例する　＝　二次

です。たとえば、練習時間の２乗と、練習成果が比例するなら、二次、です。なので、上の話、「練習量と成果は比例しない」ということを言いたいなら、

練習時間の３乗と、練習成果が比例する（つまり、３次）

でも、

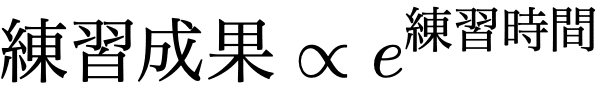
と指数関数に比例しても（８の時の横倒しみたいな記号は比例の意味です）でもよいわけです。

一次の関係は「線形」ともいいます。原因と結果が直接結びつく場合ですね。それに対して、二次とか三次、あるいは指数関数的な変化は、非線形な関係といいます。これは原因と結果が関係していて、さらに結果が原因に関係する（フィードバックする）ような場合によく現れます。

たとえば、自転車の練習でいえば、練習した結果、少し強くなり、その結果、より強度の高い練習ができるようになる、みたいなのときには、練習量を２倍したら、成果が２倍という比例関係よりも、成果が３倍とか４倍とかになります。

まあ、上のブログの「二次曲線の法則」というのはこういうことを言いたいのだと思います（でも、用語は正しく使わないと。。。）。

ちなみに、グラフが「曲線になる」というのは二次曲線を表しているわけではありません。Wikipediaの両対数グラフのところを見てみましょう。

ここには３種類直線が書かれていますが、青線は１次、緑は２次、赤は３次曲線です。縦軸・横軸を対数で書いているから直線になるのです。

（了）