最近、理系になじみのないひとが周りに増えてきてた。かれらは「数学なんかできなくても生きていけるし！」的なことをよくいうのだが、まぁそうなのかもしれないとおもいつつも、やっぱりずっと数式をいじってきた人間としてはさみしいものをかんじる。
　こうしたことは数学だけに限らない。学問全般で「この知識が生活の○○に役立つ」とか、そういう発想はやめた方がいいというのがぼくの持論だ。学問がなんの役に立つのか？という大きな問題について思うところはないわけではないのだけれど、それに関してのコメントは今回は控えたい。とにかく＜なにかに役立てるために＞学問をする、というのはやっぱりなんか気持ちが悪い。もちろん、実学的な研究ではそうなのだろうけど、目的に合わせて学問を間引くみたいな発想を、ぼくはどうも貧困さをかんじてしまう。

　役に立つとか立たないとかとどれだけ関係があるのかはわからないけれど、とにかく「学問と感覚」の話題はしておいた方がいいと思った。
　そこで今回は数学の話をしてみることにした。モンティ・ホール問題という有名な問題を題材に、数学の感覚についての話をする。

「モンティ・ホール問題」とは？

　そもそもこの名前を聞いたことがないというひとももちろんいるだろう。元ネタはアメリカのテレビ番組かなにからしいのだが、以下のような問題としてモンティ・ホールは知られている。

「プレイヤー（回答者）の前に閉じられた3つのドアが用意され、そのうちの1つの後ろには景品が置かれ、2つの後ろには、外れを意味するヤギがいる。プレイヤーは景品のドアを当てると景品をもらえる。最初に、プレイヤーは1つのドアを選択するがドアは開けない。次に、当たり外れを事前に知っているモンティ（司会者）が残りのドアのうち1つの外れのドアをプレイヤーに教える（ドアを開け、外れを見せる）。ここでプレイヤーは、ドアの選択を、残っている開けられていないドアに変更しても良いとモンティから告げられる。プレイヤーはドアの選択を変更すべきだろうか？」
引用元：モンティ・ホール問題 - Wikipedia

　この問題は「残った２つのうちのどっちかがアタリなんだから、確率はドアを変えようが変えまいが1/2なんじゃないの？？」というふうに直感的に思えてしまうのだが、答えは1/2にはなってくれない。

極端な例を考える

　確率の問題の一番愚直な解法は樹形図を書くことだが、そんな七面倒くさいことをするつもりはない。サクッとザックリ解いていきたい。

　そもそも、モンティがいらんことをしなければ勝率は1/3だ。この問題の気持ち悪いところは、モンティがちょっかいをかけることで勝率が変わることだ。テキトーに選んで勝率1/3だったものが、モンティがドアを開けることでなぜ1/2になるのか？　勝率が変わるなら、どのように変わるのか？

　こういうときの鉄則は「極端な例を考える」ということだ。
　たとえばドアの数を１００００個あったとする。そのなかでアタリはやっぱり１つ。そしてモンティはアタリと挑戦者が選んだドアを残してぜんぶ開けます（9998個のドアを開ける）。
　そしたらどうだろう？　勝率は本当に1/2だろうか？
　これ、ドア変えた方が勝つじゃん。
　だって、一発目の選択で1/10000を引き当ててるとか、常識的に考えない。最初じぶんが引いたものはアタリのはずがない、そう考えると、残った１つのドアに選択を変えることは自分が選ばなかった9999個のドアを選んだことに等しいと考えられる。

　ここでもとのドア３つの問題に戻る。起こっていることはドアが何個だろうが同じだ。なので、

ドアをモンティが開けた後に変更したら、最初に選ばなかったドアをすべて選んだのと同じ勝率

　という仮説が立つ。

ドアを変えない→勝率1/3
ドアを変える　→勝率2/3

　となる。

もう少し厳密に

　前章の仮説は感覚的には理解できるが、しかし厳密さがないっていうことに不満を抱くフレンズも多いだろう。そこで数式をちょこっと使ってこの問題を考えてみたい。

　まず、扱う数字の定義からはじめる。
　ここで、各事象と数字をまとめて奥。ドアがそれぞれ①、②、③の番号がついているとして,

C1, C2, C3：それぞれドア①,②,③がアタリである事象
M1, M2, M3：モンティが挑戦者のあとにそれぞれドア①,②,③を開く事象
X*：事象Xが起こらない事象
X∩Y：事象Xと事象Yが同時に発生する事象
P(X)：事象Xが発生する確率
P(C1)=P(C2)=P(C3)=1/3

　ここで、「モンティがドアを開いた後、ドアを変えたときの勝率」ってどうやって表せばいいのかを考える。
　数学で最もといっていいほど重要なのは、こういう感じで問題を読みかえる力だとぼくは思う。「読みかえる」というとちょっと語弊があるかもだけど、これは事象をモデル化する力（いわゆる「モデリング」）ともいうだろう。

特殊なケースを考える

　ここでさっきにやった「極端な例を考える」と似ているが、特殊なケース（＝具体的なケース）を考えてみたい。だいたいのことは一般のことを考えるのはむずかしくて、アインシュタインも相対性理論はまず「特殊」からはじめて「一般」を完成させたが、まぁそんな感じだ。

　数学におけるこ「特殊」とは、「ある変数を固定する」という手続きをとることだ。というわけで、

挑戦者は①を選ぶ
モンティは②を選ぶ

　というケースを以下では考えるとする。
　じっさい、重要なのは彼らが何番を選ぶかじゃなく、彼らが選んだドアがアタリかハズレか、ということで、答えを知らない挑戦者からしたらどのドアも勝率は1/3になる。だからもう選ぶドアを固定してしまっても、これから求める確率には影響がでない。これを「一般性を失わない」という。ちょっとした決めゼリフだ。

条件付き確率

　ここで以下のような確率を導入する。

ある事象Ｂが起こるという条件の下で事象Ａが発生する確率を
P(Ａ|Ｂ)
と書く

　これを「条件付き確率」という（これはとりあえず「後だしジャンケン」だと思ってもらえればＯＫ）。
図に書くとこんな感じ↓

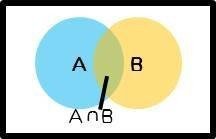
　単に「ＡとＢが同時に起こる」なら、P(A∩B)となるけれど、

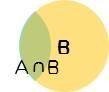
　条件付き確率では、P(B)という<全体>のなかでP(A∩B)が発生する確率を示す。
　だから一般に

P(A|B)  =  P(A∩B)/P(B)

　となる。また、上の定義に加え、準備として「ベイズの定理」も記しておく。

P(A∩B) = P(B∩A) なら
P(A|B) = P(A)/P(B) × P(B|A) 

　これを使うと、選択を変えたもの（=③のドア）がアタリの確率はベイズの定理より、

P(C3 | M2)    =　P(C3) P(M2|C3) / P(M)

　ここで、事象M2はいつも挑戦者が選んだドアに依存するため、考えられるすべての事象を足し合わせる。「モンティは必ず外す」という前提を使って式を計算していくと、 

P(M2)　　　  =　P(C1)P(M2|C1) + P(C2)P(M2|C2) + P(C3)P(M2|C3)
　　　　　     =　1/3 × 1/2  +  1/3 × 0  +  1/3 × 1
　　　　　     =　1/2

　となるので

P(C3 | M2)　　　=　1/3 × 1 / (1/2)
　　　　　　 　　=　2/3

　これで極端なケースを考えて立てた仮説

「ドアをモンティが開けた後に変更したら、最初に選ばなかったドアをすべて選んだのと同じ勝率」

　と同じ数字を得ることができました（注：今回は仮説そのものを証明したわけではありません）。

おわりに

　あまり上手な説明とはいえない上に、だいぶ危なっかしいロジックかもしれないが、なんとな～くでも理解してもらえるとうれしい。
　まぁ、なにが言いたいかって、モンティ・ホールや条件付き確率云々は、それ自体超おもしろいことがたくさん詰まっているのですが、ひとまずここでは割とどうでもいい話だ。

　この問題を考えるにあたって使ったテクニックである、

・極端な例を考える（極限をとる）
・特殊なケースを考える（対称性を使う）

　というのは、院生時代にボスからちょくちょく言われてきたけれど、リケーだのブンケーだの関係なしに大切なことだと個人的に思っている。
　ぼくとかは極限や対称をまず考えたりするのだが、それを思い浮かべるだけで（ものによっては）だいたい答えがわかったりする。それが数学の感覚なのかもしれないが、なにかを思考する、というプロセスじたいに、今回話した範囲では「数学の特異性」みたいなのはない気がする。ぼくはそう信じたい。

　あと、今回は数式を扱った。数式は慣れないとキツいけれど、あれは目の前で起こっていることを表現する言語だと思えば、少しは数学アレルギーがとれるんじゃないかなって思う。
　なにより数式いじりは結構たのしい。今回興味を持たれたかたは、ぜひ紙とペンで遊んでいただければ幸いです。

参考文献↓