因果推論と Statistical Matching の基礎のお勉強メモ
因果推論の基本
ルビンの潜在反応モデルでは、ある人物に介入した時の反応($${Y_1}$$)と介入しなかった時の反応($${Y_0}$$)の差を介入の因果的効果と見做します。
しかし、現実には同一人物で介入をした場合としなかった場合を同時に観測することはできずません。(影分身してもらわないといけません。)
そこで、個人ではなく集団における平均的な因果効果として$${E[Y_1 - Y_0] = E[Y_1] - E[Y_0]}$$ (これを ATE: Average Treatment Effect と呼ぶ)であれば推定できないかを考えます。これは次式のように分解することができます。ここで $${T}$$ は介入をするかどうかを示す変数で、$${T = 1}$$ は介入したことを、$${T = 0}$$ は介入されなかったことを示します。
$$
\begin{align*}
&E[Y_1|T=1] - E[Y_0|T=0] \\[5pt]
&= E[Y_1| T=1] - E[Y_0|T=1] + E[Y_0|T=1] - E[Y_0|T=0] \\[5pt]
&= E[Y_1 - Y_0 | T = 1] + E[Y_0|T=1] - E[Y_0|T=0] \end{align*}
$$
3 式の $${E[Y_1 - Y_0 | T = 1]}$$ は介入されたグループの中での因果効果の大きさで、ATT: Averate Treatment Effect on Treatedと呼びます。残る $${E[Y_0|T=1] - E[Y_0|T=0]}$$ は選択性バイアスと呼ばれます。 treatment group, control group それぞれにおける期待値の差は、ATT + 選択性バイアスに分解できるということになります。残念ながら介入があったグループ(treatment group)において、仮に介入がなかった場合の反応の期待値( $${ E[Y_0|T=1] }$$ )はデータとして手に入りませんので、このままでは算出することはできません。
もし介入の有無と反応は独立($${ {T \mathop{\perp\!\!\!\!\perp}(Y_1, Y_0)} }$$)とさせた A/B テストを行うことができれば、
$$
E[Y_1|T=1] = E[Y_1|T=0] = E[Y_1] \\[5pt]
E[Y_0|T=1] = E[Y_0|T=0] = E[Y_0]
$$
となるため、
$$
\begin{align*}
ATE &= E[Y_1|T=1] - E[Y_0|T=0] \\[5pt] &= E[Y_1] - E[Y_0]\end{align*}
$$
と計算できます。なおこの時選択性バイアスは
$$
E[Y_0|T=1] - E[Y_0|T=0] = E[Y_0] - E[Y_0] = 0
$$
上記のように 0 であるため、ATT = ATE となります。しかし、A/B テストが行えず観察データから推定しないといけない場合にはこのように簡便な計算で済ませることはできません..。
共変量を用いるアプローチ
この時に、「条件つけることで$${ {T \mathop{\perp\!\!\!\!\perp}(Y_1, Y_0)} }$$ となるような共変量」 $${ Z }$$ が特定できデータも手に入る場合には、工夫をすることで因果的効果を求めることができます。
(なお、$${ {T \mathop{\perp\!\!\!\!\perp}(Y_1, Y_0)} | Z }$$ であることは強い意味で無視可能である, strongly ignorable と言います。)
$${ {T \mathop{\perp\!\!\!\!\perp}(Y_1, Y_0)} | Z }$$ であれば、(Zが同じであれば T がどんな値を取ろうが Y には影響しないため)$${ E[Y_0|T=1, Z=z] = E[Y_0|T=0, Z=z] = E[Y_0|Z=z] }$$が成り立つことになるので、 $${ Z }$$ で条件つけた時の選択性バイアスは 0 になります。 $${ E[Y_0|T=1, Z=z] - E[Y_0|T=0, Z=z] = 0 }$$
ですので、そのような状況であれば共変量を用いてさまざまな方法で、選択性バイアスにとらわれず効果を推定することができます。
e.g., 回帰分析
$${ E[Y|Z, T ] = \beta_0 + \beta_1 Z + \beta_2 T }$$ のような形で Z, T のもとでの Y の条件付き期待値を回帰モデルで推定する
e.g., 層別解析
$${E[Y_1|T=1, Z=z] - E[Y_0|T=0, Z=z] = E[Y_1|Z=z] - E[Y_0|Z=z] }$$
であるのでこれを、Z について期待値を取れば、$${ E_Z[E[Y_1|Z=z] - E[Y_0|Z=z]] = E[Y_1] - E[Y_0]}$$ と ATE を得られる。これは Z の値ごとにサブグループをつくり、各グループで効果を推定し(treatment と control で反応の期待値の差をとる)、サブグループで重み付けた和を取るということ
e.g., マッチング
Treatment Group の各ユーザーについて、Control Group から共変量が一致している人を探してきてペアをつくり、その人の反応を反実仮想のデータとて $${ Y_1 - Y_0 }$$ を計算し全体で平均をとる
今回はマッチング法について掘り下げてメモします。
Statistical Matching
先述の通りマッチング法は Treatment Group の各ユーザーについて、Control Group から共変量が一致している人を探してきてペアをつくり、その人の反応を反実仮想のデータとて $${ Y_1 - Y_0 }$$ を計算し全体で平均をとります。Treatment Group の人の $${ (Y-1, Y_0) }$$ を比較するため基本的には ATT を得ることができます。ですが、同様のことを Control Group に対して行い合算すれば ATE も算出可能です。
ただし、マッチングの場合には必ずしもすべてのサンプルについてマッチング対象が見つかるとは限りません。例えば下記のようにデータが散らばっていた場合には、$${ Z \geq 2, Z \leq-2}$$ の範囲についてはマッチング相手が存在せずこのデータは切り捨てられることになります(マッチングの方法では必ず相手を見つけることもできます)。ですので、その場合に求められる効果はあくまでペアが存在する中での効果となり全てのデータを使って計算する ATT, ATE とは意味合いが少し異なります。

さまざまなマッチング方法
ペアを見つけてくるにはたくさんの考え方があります。
一番単純なのは、共変量がまったく同じ値のものをマッチング対象とするもので、これは厳密なマッチングといい、後の実装では `method = "nearest"` で指定できます。
厳密なマッチングでは、(特に連続変数が入っていると)全くマッチしないこともあるため、条件を緩めて共変量で距離が近い近傍点をマッチング対象とする方法があります。これは最近傍マッチング、といいこの時に使う距離は例えばマハラノビス距離などを使えます。マッチング相手が複数見つかった場合には、複数の平均をとるか、ランダムに 1 人ピックアップしてその人の値を利用するなどします。
一番近ければ誰でもよい、というわけでなく一定の閾値の距離の範囲内であればみなマッチング相手とみなすような考え方はカリパーマッチングと言い、こちらも指定できます。
他、こちらに案内があります。
共変量の次元削減
共変量の数が多くなるほどマッチング対象を見つけるのは難しくなります。
そこで、多数の共変量を傾向スコア(Propensity Score)という 1 つの変数に次元削減してしまう考え方があります。傾向スコアは $${ e(z) = P(T=1|Z=z) }$$ と、共変量 Z で条件つけたときに介入を受ける確率です。
傾向スコアに関しては下記の 2 つの重要な定理があります。
傾向スコアのバランシング性:傾向スコアを与えた時、介入 $${T}$$ と共変量 $${Z}$$ は条件付き独立になる
傾向スコアの無視可能性の保存:介入 $${T}$$ が共変量 $${Z}$$ を与えたもとで強い意味で無視可能であるならば、$${T}$$ は傾向スコア $${e(z)}$$ を与えたもとで強い意味で無視可能である。
上記におかげで、適切な傾向スコアが得られれば、生の共変量の代わりに傾向スコアを使って問題ありません。
傾向スコア自体は、$${T}$$ を目的変数, $${Z}$$ を説明変数としてロジットモデルなどで得られます。
共変量間の距離でマッチングする部分を傾向スコアで代替することができそれば傾向スコアマッチングと呼びます。マッチング以外にも、傾向スコアで層別解析したり、傾向スコアの逆数で各サンプルを重み付けして比較する IPW などさまざまな活用方法があります。
R を用いた実装方法
R でマッチングを行えるパッケージには、MatchIt や Matching があります。可視化が行いやすかったので MatchIt について MatchIt のチュートリアルなどを参考に使い方の部分をメモします。
データはパッケージに組み込みの lalonde データセットを用います。今回は動かし方をみるためなので、データの詳細は割愛します。
library(MatchIt)
data("lalonde")Step1: Initial Imbalance の確認
まずはマッチングする前の状態でどれだけバランスが取れているかどうかを確認します。介入の有無にかかわらず共変量の分布が変わらない状態が、バランスが取れている状態です。
matchit 関数で共変量のバランスを確認することができます。formula 引数に、T ~ Z といった形で介入の変数と共変量を指定します。Matching もこの関数で行いますが、Matching をしない場合は、method = NULL を指定します。
m_init <- matchit(
formula = treat ~ age + educ + race + married + nodegree + re74 + re75,
data = lalonde,
method = NULL
)
summary(m_init)
"""
Summary of Balance for All Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance 0.5774 0.1822 1.7941 0.9211 0.3774
age 25.8162 28.0303 -0.3094 0.4400 0.0813
educ 10.3459 10.2354 0.0550 0.4959 0.0347
raceblack 0.8432 0.2028 1.7615 . 0.6404
racehispan 0.0595 0.1422 -0.3498 . 0.0827
racewhite 0.0973 0.6550 -1.8819 . 0.5577
married 0.1892 0.5128 -0.8263 . 0.3236
nodegree 0.7081 0.5967 0.2450 . 0.1114
re74 2095.5737 5619.2365 -0.7211 0.5181 0.2248
re75 1532.0553 2466.4844 -0.2903 0.9563 0.1342
eCDF Max
distance 0.6444
age 0.1577
educ 0.1114
raceblack 0.6404
racehispan 0.0827
racewhite 0.5577
married 0.3236
nodegree 0.1114
re74 0.4470
re75 0.2876
"""`Summary of Balance for All Data:` の箇所で、共変量ごとに統計量を見るととができます。注目する箇所は下記です。
Std. Mean Diff.: Treatment Group と Control Group 間の共変量の標準化された平均値差です。これは 0 に近いほど良い値です。普遍的な基準はありませんが、こちらでは 0.1 未満であるとよいとされています。
Var. Ratio: Treatment Group と Control Group 間の共変量の分散比です。これは 1 に近いほど良い値です。
Step2: Matching
matchit 関数を用いてマッチングを実行します。この際にオプションでマッチング方法を下記のように指定できます。
# 厳密なマッチング: method="exact"
m_exact <- matchit(
treat ~ age + educ + race + married + nodegree + re74 + re75,
data = lalonde,
method = "exact"
)
# マハラノビス距離による最近傍マッチング: method="nearest", distance="mahalanobis"
m_mahalanobis <- matchit(
treat ~ age + educ + race + married + nodegree + re74 + re75,
data = lalonde,
method = "nearest",
distance = "mahalanobis"
)
# 傾向スコアで最近傍マッチング
m_ps <- matchit(
treat ~ age + educ + race + married + nodegree + re74 + re75,
data = lalonde,
method = "nearest",
distance = "glm",
)傾向スコアマッチングにおいては、distance はデフォルトの "glm" ではロジットモデルで傾向スコアを推定します。他にも "gam" で一般化化加法モデルや、"randomforest" でランダムフォレストなどが使用できます。
効果推定の際に関係してくる内容として、マッチングを復元抽出か非復元抽出で行うかというトピックがあります。treatment group の各個人に対して順にペアを探していくわけですが、1 度マッチした相手は別の個人のペア候補には含めないようにするのが非復元抽出、再度ペア候補に含めるのは復元抽出になります。これは `relace = TRUE, FALSE` と引数で設定することができ、デフォルトは FALSE(復元抽出)です。
非復元抽出を設定した場合には、control group 内のある個人が複数人に対してマッチする可能性があり、マッチングされたデータが独立でなくなるため効果推定の際にそれを考慮する必要があります。
Step3: Quality of Matches の確認
マッチングにより共変量のバランスが取れたかどうかを確認します。
① 任意の共変量について Treatment / Control ごとに分布を確認
cobalt パッケージの bal.plot で任意の共変量について可視化を行えます。
library(cobalt)
library(ggplot2)
bal.plot(m_ps, var.name = "re74", which="both", type="histogram", mirror=FALSE)
+ theme_minimal()

例えば re74 という共変量については、マッチング前に比べてマッチング後には共変量バランスがとれていることが視覚的に確認できます。
② Absolute Mean Differences が望ましい値のレンジに収まっているかどうかを確認
love.plot ですべての共変量について Std. Mean Diff の値のマッチング前後の比較を可視化できます。
love.plot(
m_ps,
threshold = 0.1,
abs = TRUE,
grid = TRUE,
# stats = c("mean.diffs", "variance.ratios") こちらを指定すると平均値差以外の指標もプロットできます。
)
+ theme_minimal()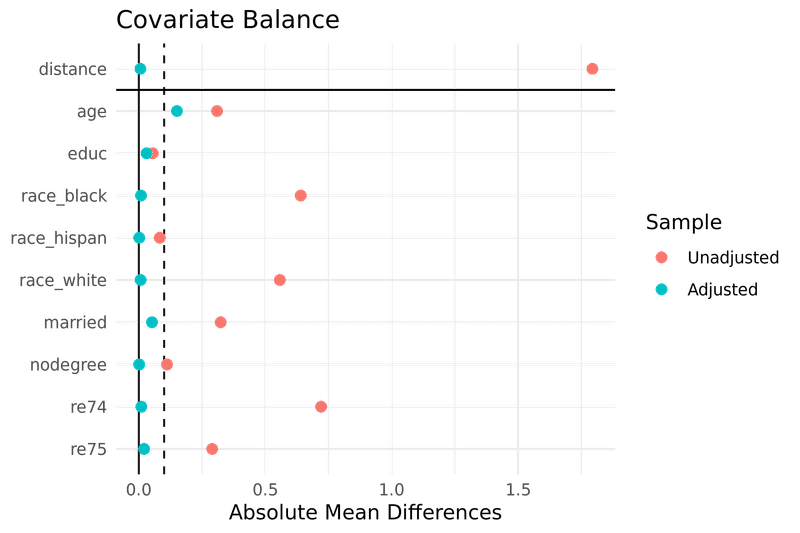
age 以外は閾値の 0.1 より左側に収まっておりバランスが取れたことがわかります。具体的な平均値差などは summary() の出力に含まれる Summary of Balance for Matched Data から確認できます。
summary(m_ps)
"""
...
Summary of Balance for Matched Data:
Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
distance 0.5774 0.5761 0.0061 0.9917 0.0041
age 25.8162 24.7372 0.1508 0.4859 0.0827
educ 10.3459 10.2846 0.0305 0.5696 0.0224
raceblack 0.8432 0.8347 0.0236 . 0.0086
racehispan 0.0595 0.0611 -0.0070 . 0.0017
racewhite 0.0973 0.1042 -0.0234 . 0.0069
married 0.1892 0.1371 0.1329 . 0.0520
nodegree 0.7081 0.7068 0.0030 . 0.0014
re74 2095.5737 2144.8386 -0.0101 1.3198 0.0399
re75 1532.0553 1598.8210 -0.0207 1.8985 0.0701
eCDF Max Std. Pair Dist.
distance 0.0486 0.0192
age 0.3212 1.2869
educ 0.0617 1.2522
raceblack 0.0086 0.0324
racehispan 0.0017 0.5555
racewhite 0.0069 0.4168
married 0.0520 0.4806
nodegree 0.0014 1.0135
re74 0.2447 0.8626
re75 0.2481 0.8179
...
"""
なお、summary() の出力には次のように Sample Size も得られます。ここからは Treated 185 サンプルの全てに対してマッチング相手が見つかった(Matched = 185)ことがわかります。
Sample Sizes:
Control Treated
All 429. 185
Matched (ESS) 52.96 185
Matched 429. 185
Unmatched 0. 0
Discarded 0. 0
Step4: 効果の推定
マッチング後データを取得し、そこから知りたい効果の大きさを計算します。match.data ではデフォルト引数では drop.unmatched = TRUE とマッチしなかったサンプルを除いたデータを取得できるのでこちらで treatment と control 間の期待値の比較してみます。(これは復元抽出でマッチングしていて、マッチング後データが独立である場合のみ可能です。)
m_data <- match.data(m_ps)
mean(m_data$re78[m_data$treat==1]) - mean(m_data$re78[m_data$treat==0])
"""
894.3675
"""
単に期待値の差分をとるのでなく、介入を説明変数として、反応を目的変数とした回帰モデルとして係数を見れば、信頼区間も得られます。非復元抽出でマッチングした場合は、この際に weights を指定してあげる必要があります。
fit <- lm(
re78 ~ treat,
data = m_data,
weights = weights
)
summary(fit)$coef
"""
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5454.7760 516.3964 10.563157 5.876044e-23
treat 894.3675 730.2948 1.224666 2.214843e-01
"""ただし、マッチングが完璧に行われていない場合は多少共変量の影響が残ってしまっていることが考えられますので、回帰式で共変量を調整することでより正確な効果を知ることができます。処置変数との交互作用項も含めて調整した上で結果を見ると 734.39 と先ほどより小さい値を得られました。
fit <- lm(
re78 ~ treat * (age + educ + race + married + nodegree + re74 + re75),
data = m_data,
weights = weights
)
summary(fit)$coef
"""
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.382837e+03 4529.5264697 -0.74684123 0.45565795
treat 7.343989e+02 6849.2030907 0.10722399 0.91467237
"""なお、チュートリアル上ではマッチング後の効果の推定については G-computation という時間依存変数が含まれた場合でも対応できる推定方法であったり、標準誤差は「誰と誰がペアになっているか」の情報を組み込んで頑健性を増す Cluster-robust standard errors なるものを推定したりと複雑なことをやっています。
詳細はこちらにあり、なかなか頭が追いついていきませんがゆっくりと理解していきたいです。
Reference
星野匡郎, 田中久稔 R による実証分析
宮川 雅巳 統計的因果推論―回帰分析の新しい枠組み―
高橋 将宜 統計的因果推論の理論と実装
Peter C. Austin An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies
MatchIt 4.5.0 Documentation
最後まで目を通していただきありがとうございました。もし内容に誤りを見つけていただいた場合はご指摘いただけますと幸いです🙇♂️
この記事が気に入ったらサポートをしてみませんか?
