相関から一歩進んで因果を調べたい時の共変量の選択基準について
回帰分析や傾向スコアを用いて因果推論をする際には、何を共変量として考慮する必要があるのか特定する必要があります。その考え方については、「統計的因果推論 -回帰分析の新しい枠組み- 」で大変わかりやすく丁寧に解説がされており、そちらでのお勉強のメモを残しておこうと思います。
相関を因果と見做すためには
$${X}$$ と $${Y}$$ の間に相関関係があったとしてもそこに因果関係があるとは限りません。例えば次のような関係性の第三の変数 $${Z}$$ が存在する場合には、$${X}$$ と $${Y}$$ が相関関係を持ってしまします。このような関係性を擬似相関と言います。

ですので、相関関係が見つかった -> これは因果関係として捉えて良い?と考える時にそれが擬似相関でないかどうかをチェックする必要があります。
その際には先ほどのような擬似相関を生み出す第三の変数(群)を考慮に入れた上でもまだ $${X}$$ と $${Y}$$ の間の関係性が見られるかを確認することになります。例えば回帰分析でやる場合には、$${ Y = \beta_{0} + \beta_{1} X + \beta_{2} Z + \beta_{3} XZ }$$ といった形で共変量を追加してあげて、その上で $${X}$$ にかかる係数が有意であるかどうかを見る形となります。
回帰分析の場合の係数の解釈は、「他の変数の値を固定した上で対象の変数の値を 1 単位動かした時にどれだけ目的変数が変動するか」になるので、先ほどの擬似相関の例でいう $${Z}$$ が固定された場合の $${X}$$ と $${Y}$$ の関係性を見ていることになります。仮に擬似相関であれば、$${Z}$$ が固定してしまったら $${X}$$ と $${Y}$$ の関係性を示す偏回帰係数の信頼区間は 0 を含み、有意でない結果が得られることが期待されます。これは重回帰分析に限らず、目的変数が質的変数であれば例えばロジスティック回帰、目的変数・説明変数といった従属性を考えずに質的変数同士の関係を見るのであれば対数線形モデルなど、一般化線形モデル全般で使える考え方です。
実際に行う際に気になるのは、何でも関係しそうな変数をすべて共変量として考慮してよいのか、という点です。共変量として考慮に入れる、というのはその変数の値を固定する処理を行うことになるので、例えば次のような場合には問題がありそうです。

この場合は、$${Z}$$ の値を固定してしまうと、$${X}$$ がどんなに変化しようが、その変化の影響は $${Z}$$ が吸収して $${Y}$$ には伝わらないため、$${X}$$ -> $${Y}$$ の因果関係があるのかを知りたい場合にはよくない処理になります。
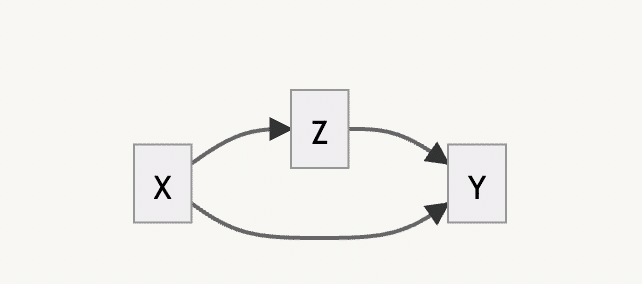
もちろん次のように $${Z}$$ を経由せずに $${Y}$$ へ影響するパスがあった場合には、効果が見られる形になりますが、それで得られる偏回帰係数は、$${X}$$ -> $${Y}$$ の総合効果ではなく、直接効果のみとなってしまいます。総合効果を知りたい場合にはやはり不適切です。
他にも共変量として取り込むと問題があるパターンがあり、そのため取り込んで問題のない変数かどうかの基準を知りたいモチベーションが生まれます。
考慮すべき共変量を選択する基準
バックドア基準
書籍から結論の部分だけをみていきたいと思います。(詳細な説明や証明はぜひ書籍を購入)
まずは総合効果を知るモチベーションにおいて、何が必要かという点について次の定理が挙げられています。
【定理6.2】偏回帰係数と総合効果の一致条件
非巡回有効グラフであるパスダイアグラム $${G}$$ において, $${X}$$ から $${Y}$$ への有向道があるとする. $${G}$$ において頂点集合 $${S}$$ が$${(X, Y)}$$ に対してバックドア基準を満たすならば, $${Y}$$ を目的変数, $${X}$$ と集合 $${S}$$ に含まれるすべての変数を説明変数にした回帰モデルでの $${X}$$ の偏回帰係数 $${ \beta_{yx・S}}$$は, $${X}$$ から $${Y}$$ への総合効果と等しい.
すなわち回帰モデルの偏回帰係数として解釈するにおいては、バックドア基準を満たす変数をモデルに組み込めばよいということになります。加えて、こちらで触れている「強い意味で無視可能である」こととバックドア基準を満たすことは等価であるとされています。([1] p.86 を参照)
https://note.com/dmaruyama/n/n25abba1278d8
ではキーワードとなっているバックドア基準とは何でしょうか。そちらは下記のように定義されています。
【定義 5.3】 バックドア基準
因果ダイアグラム $${G}$$ において、$${X}$$ から $${Y}$$ へ有向道があるとする. このとき, 次の 2 つの条件を満たす頂点集合 $${S}$$ は, $${(X, Y)}$$ についてバックドア基準を満たすという.
1. $${X}$$ から $${S}$$ への任意の要素へ有向道がない。
2. 因果ダイアグラム $${G}$$ より $${X}$$ からでる矢線を除いたグラフにおいて、$${S}$$ が $${X}$$ と $${Y}$$ を有向分離する。
2 つの条件が提示されており、1 つ目が意味することは、$${X}$$ から $${Y}$$ への因果を知りたい時に $${X}$$ から出る矢印の先にある変数は考慮しなくてよい、ということです。
そしそれ以外については、$${X, Y}$$ を有向分離する変数であれば採用してよい、そうでなければ不採用という判断基準となっています。
有向分離
では有向分離とは何でしょうか。
【定義 4.3】有向分離
非巡回的有効グラフ $${G = (V, E)}$$ を考える. 2 つの頂点 $${\alpha}$$ と $${\beta}$$ を結ぶすべての道のそれぞれについて、{$${\alpha}$$, $${\beta}$$} と排反な頂点集合 S が次の条件のいずれかを満たすとき, S は $${\alpha}$$ と $${\beta}$$ を有向分離するという.
1. $${\alpha}$$ と $${\beta}$$ を結ぶ道上の合流点で、その合流点とその子孫が S に含まれないものがある。
2. $${\alpha}$$ と $${\beta}$$ を結ぶ道上の非合流点で、S に含まれるものがある。
なお、$${\alpha}$$ と $${\beta}$$ を結ぶ道がないときは、空集合が $${\alpha}$$ と $${\beta}$$ を有向分離するという。
条件 2 は、 $${X}$$ -> $${Y}$$ の道の途中にある変数は、$${X}$$ と $${Y}$$ を有向分離する変数であるということを意味しています。この変数群はバックドア基準の 1 つ目の条件に反するため、有向分離する変数ではあるのですが、不採用になります。また、冒頭で紹介したような(Z -> X, Z ->Y の)分岐パターンも $${Z}$$ が $${X, Y}$$ を有向分離する変数であることを意味しています。
条件 1 については 3 変数の場合は、「選択による偏り」と言われる擬似相関のパターンでは有向分離しないことを意味しています。選択による偏りは次のようなケースで、$${Z}$$ で固定した際に $${X}$$ と $${Y}$$ に相関が生まれてしまうことを指します。

これはぱっと見なんで擬似相関?と思うのですが、例えば矢印が「矢印の元の変数に x 1 倍するような変換をする」処理を表してると考えてみると、
$$
Z = X \times 1 + Y \times 1 = X + Y
$$
$$
Y = Z - X
$$
というような $${X}$$ と $${Y}$$ の関係性となります。相関関係とは、$${X}$$ が大きくなったら $${Y}$$ も線形に大きくなる(あるいは小さくなる)というような関係性のため、例えば $${X}$$ を大きくしたり小さくしたりした時に、$${Z}$$ の値が仮に固定されていればその変動がそのまま $${Y}$$ に影響してしまうことがわかります。逆に $${Z}$$ が固定されていなければ、$${X}$$ をどんなに動かそうと $${Z}$$ が自由に動けば $${Y}$$ へ単調な影響を与えなくすることができます。
多変数間で考慮した際に、[1] p.69 では条件 2 における注意すべきパターンとして、M 字形と W 字形に触れられています。
M 字形とは次のようなケースです。

この時に $${(X_1, X_2)}$$ を有向分離しない変数は $${Z_{3}}$$ のみとなります。(ですので、$${Z_{3}}$$ を共変量として採用してしまうのは NG となります。)
イメージとしては、$${Z_{3}}$$ を固定すると、選択による偏りで $${(Z_{1}, Z_{2})}$$ が相関を持つため、その先にある $${(X_1, X_2)}$$ も相関を持ってしまう形となります。
先ほどのように矢印が「矢印の元の変数に x 1 倍するような変換をする」処理を表してるとすると次のようになります。
$$
Z_3 = Z_1 + Z_2 = X_1 + X_2
$$
$$
X_2 = Z_3 - X_1
$$
ですので、$${Z_3}$$ を固定してしまうと(定数扱いにしてしまうと)、 $${(X_1, X_2)}$$ が相関を持ってしまうことがわかります。
次に W 字形は次のような形です。

W 字形で $${(X_1, X_2)}$$ を有向分離しない変数は $${(Z_{2}, Z_{3})}$$ になります。(ただ、有向分離するにせよしないにせよ、このケースの $${Z_1, Z_2, Z_3}$$ はバックドア基準を満たしません。)
イメージとしては、例えば $${Z_2}$$ だけ固定した場合には、$${(X_1, Z_1)}$$ は相関を持つが $${Z_3}$$ を固定していないため $${(Z_1, X_2)}$$ は相関を持たない。しかし $${Z_3}$$ も合わせて固定してしまうと $${(Z_1, X_2)}$$ が相関を持つため、$${(X_1, Z_1)}$$ の相関と合わせて $${(X_1, X_2)}$$ も相関を持ってしまうという形です。
矢印が「矢印の元の変数に x 1 倍するような変換をする」処理を表してると仮で考えると、
$$
\begin{align*}
&Z_2 = X_1 + Z_1 \\
&Z_3 = Z_1 + X_2 \\
&Z_1 = Z_2 - X_1 = Z_3 - X_2 \\
&X_2 = X_1 + Z_3 - Z_2
\end{align*}
$$
というような関係性となり、$${Z_2, Z_3}$$ の両方を固定してしまうと(定数としてしてしまうと)、 $${X_1}$$ の変化がそのまま $${X_2}$$ に影響してしまうことがわかります。
無視してよい変数
[後ほど追記]
- バックドア基準を満たす変数が複数ある場合、無視してよいものがある & パス係数の分散をより小さくできる選択肢
- 未知の交絡がある場合
おわりに
バックドア基準に関する資料としては、他に参考資料 [2] のスライドはイメージでバックドア基準を掴むとてもわかりやすいものでした。また実践的な共変量の選択のアプローチを紹介している [3] もとても勉強になりました。
Reference
[1] 宮川 雅巳 統計的因果推論―回帰分析の新しい枠組み―
[2] [3] https://www.krsk-phs.com/entry/counfounder_selection
最後まで目を通していただきありがとうございました。もし内容に誤りを見つけていただいた場合はご指摘いただけますと幸いです🙇♂️
この記事が気に入ったらサポートをしてみませんか?
