第10章「え！そっちに入れるんですか？」のベイズモデリングをPyMC Ver.5 で

ネイピア DS

2024年4月6日 10:14

この記事は、テキスト「たのしいベイズモデリング２」の第10章「え？そっちに入れるんですか？」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

この章では、選挙において人々が「政策争点」に基づいて投票を行う「争点投票」をモデル化します。
数理モデルに基づく３つのモデルを構築して、モデル間比較やパラメータを確認します。
今回の PyMC化は、まずまずの出来です！

ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　宋財泫先生、矢内勇生先生
モデル難易度：　★★・・・　（やさしめ）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい！ \\
\end{array}
$$

評価ポイント

３回連続でテキストの結果とほぼ一致！
嬉しいです！！！
最初にテキストを流し読みしたとき、「数理モデルかぁ、なんだか難しそうだよな・・・」とPyMC化の難易度が高そうな印象を受けて、投げ出そうかと考えました。
しかし、テキストの精読とR＆Stanコード読み込みを通じて、案外ハードルは高くないなと納得して、何とかPyMCモデルにリーチできました。

工夫・喜び・反省

「伸縮近接性モデル」の効用関数に用いられる$${\tilde{V}_i,\ \tilde{P}_k}$$をPyMCモデルで定義するのが難しかったです。
pytensor 変数を操作する関数を作成するのにとても時間がかかりました。
サンプルコードの Stanコードが R の「rds ファイル」で格納されていたので、取り出しに苦労しました（汗）

モデルの概要

テキストの調査・実験の概要

■ 争点投票
選挙で有権者がどのように政党や候補者を選ぶかについて、テキストのモデリングは「争点投票」を前提にしています。
争点投票は「有権者は自分が望む政策を実現してくれると思える政党や候補に投票する」という投票行動です。

■ 争点空間
テキストにならい、「消費税率」を政策争点の例にして争点空間のイメージを考えてみます。
次の図は１次元の争点空間のイメージ図です。
空間と呼ぶとなんだか難しいものに感じるので、「定規の目盛り」に見立ててみましょう。
ちなみに「尺度」を「温度」に読み替えると、温度計に見えます！

テキストの調査では、現状を０に置き、政策内容を－７から７までの「１５点尺度」を用いて表現しています。
図の消費税率の政策の例では、現状は１０％で尺度０、減税政策は尺度－１から－７までマイナス１％きざみ、増税政策は尺度１から７までプラス１％きざみで増減しています。

有権者1（$${i=1}$$）は１％減税の税率９％の政策を支持しているので、尺度－１です。
政党Ａ（$${k=A}$$）は５％減税の税率５％の政策実現を目指しており、尺度－５です。
政党Ｂ（$${k=B}$$）は２％減税の税率１２％の政策実現を目指しており、尺度２です。

この直線上の尺度の関係が１次元の政策空間を示しているのです。

■ 有権者が投票先を決める３つのモデル
上の図で１次元の尺度上（直線の尺度上）の有権者１、政党Ａ、政党Ｂのポジションが明らかになりました。
ポジションの関係から、有権者はどのように判断して投票先を決めるのでしょう？
テキストは「近接性モデル」「方向性モデル」「伸縮近接性モデル」の３つを提示しています。

■ 近接性モデル
有権者は自分の政策と近い政党、言い換えると、直線上の距離が短い政党を選ぶとするモデルです。
先程の図を利用します。

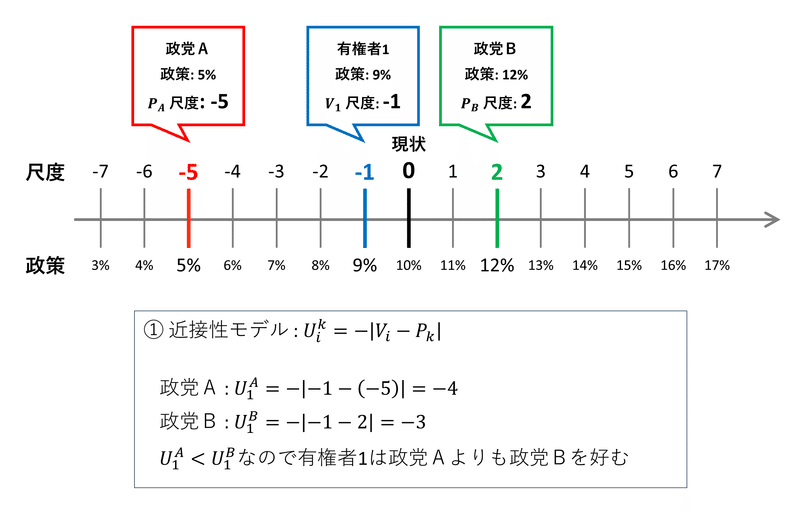
数式にすると難しそうなのですが、ざっくりこんな感じで捉えられます。

尺度－１の有権者１と尺度－５の政党Ｂの距離はー１－（－５）＝４です。
絶対値にすると４です。
尺度－１の有権者１と尺度２の政党Ｂの距離はー１－（２）＝－３です。
絶対値にすると３です。
３の方が近いので、有権者１は政党Ｂを選ぶでしょう。

■ 方向性モデル
有権者は、自分と同じ方向の政策変化を目指す政党の中で最も極端な政策を掲げる政党を選ぶとするモデルです。
先程の図を利用します。

数式にすると難しそうなのですが、ざっくりこんな感じで捉えられます。

有権者１は減税方向の政策を支持しています。
政党Ａは減税方向の政策を掲げ、政党Ｂは増税方向の政策を掲げています。
有権者１は減税方向の政党Ａを選ぶでしょう。

政党Ｃが減税７％の税率３％政策を掲げている場合を考えてみます。

減税政策を掲げる政党は、政党Ａ（税率５％、尺度－５）と政党Ｃ（税率３％、尺度－７）です。
減税方向で極端な政策を掲げるのは政党Ｃです。
したがって、有権者１は政党Ｃを選ぶでしょう。

■ 伸縮近接性モデル
方向性モデルの場合、極端な政策を選びがちであり、有権者の考える政策に近い政党よりも、もっと極端な政策を掲げる政党を選択してしまいます。
また、近接性モデルの場合、直線上の近さで選びがちであり、直線上で最も近ければ政策変化の方向が違う政党を選択してしまいます。
これらの問題を改善する１つのモデルとして、執筆の先生は伸縮近接性モデルを取り上げます。

このモデルを簡易に説明するのは困難なので、図示して逃げます！

尺度の絶対値が大きくなるにつれて距離が相対的に短くなる、という距離を持ち込んでいます。
相対的に短くなったり長くなったりする様子が距離の「伸縮」なんですね。
この伸び縮みする距離感によって、政策の方向が逆の政党よりも、政党の方向が同じ向きの政党を選びやすくするそうです。

■ 調査データの概要
１０個の争点について、調査参加者が支持する政策と尺度の回答を得て、さらに政党候補者Ａ・Ｂの政策と尺度を示して投票先の回答を得る、というオンラインサーベイ（回答者数3,139人）を実施したそうです。
テキストでは、「憲法９条改正」と「経済に関する市場対国家」の２争点を取り上げ、データクリーニング後の2,078人の回答データを利用します。

テキストのモデリング

３つのモデルに共通する部分のモデリングから書きます。
有権者が２人の候補者ＡとＢのどちらを選ぶか、に焦点を当てます。

■ 目的変数と関心のあるパラメータ
目的変数は、有権者$${i}$$が候補者Ａを選ぶ場合に 1、候補者Ｂを選ぶ場合に 0 をとる二値変数$${Y_i}$$です。
関心のあるパラメータは、①伸縮近接性モデルの伸縮度を表すパラメータ$${\omega}$$と、②効用の差$${U^A_i-U^B_i}$$です。
添字$${A}$$は候補者Ａ、$${B}$$は候補者Ｂです。

■ モデル数式

$$
\begin{align*}
y_i &\sim \text{Bernoulli}\ (\theta_i) \\
\theta_i &= \text{logit}^{-1}\ (\alpha + \beta (U^A_i-U^B_i)) \\
\alpha &\sim \text{Cauchy}\ (0,\ 100) \\
\beta &\sim \text{Cauchy}\ (0,\ 100) \\
\end{align*}
$$

テキストより引用

$${\text{logit}^{-1}}$$は逆ロジット関数です。ロジスティック関数です。
$${U^A_i}$$は有権者$${i}$$が候補者Ａの政策から得られる効用、$${U^B_i}$$は有権者$${i}$$が候補者Ｂの政策から得られる効用です。

３つのモデルは効用$${U^k_i,\ k=A, B}$$が異なります。

■ 近接性モデル

$$
U^k_i = -|V_i - P_k|
$$

テキストより引用

$${V_i}$$は有権者$${i}$$が支持する政策の尺度、$${P_k}$$は候補者$${k=A, B}$$が掲げる政策の尺度です。

■ 方向性モデル

$$
U^k_i = V_i \times P_k
$$

テキストより引用

■ 伸縮近接性モデル

$$
\begin{align*}
U^k_i &= -|\tilde{V}_i - \tilde{P}_k| \\
\\
\tilde{V}_i &= \text{sign}\ V_i\ \displaystyle \sum_{s=0}^{|V_i|-1} \omega^s \\
\tilde{P}_k &= \text{sign}\ P_k\ \displaystyle \sum_{s=0}^{|P_k|-1} \omega^s \\
\omega &\sim \text{Uniform}\ (0,\ 2)
\end{align*}
$$

テキストより引用

$${\omega}$$は距離の伸縮度を表すパラメータです。
$${\text{sign}}$$は対象変数の符号が＋のときに＋をとり、－のときに－をとる関数です。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。

PyMC実装

Let's enjoy PyMC & Python !

実装中の争点は、「憲法９条改正」を争点１、「市場vs国家」を争点２と呼んでいます。

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np
# import scipy.stats as stats

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 評価指標 
from sklearn.metrics import accuracy_score, cohen_kappa_score

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込み
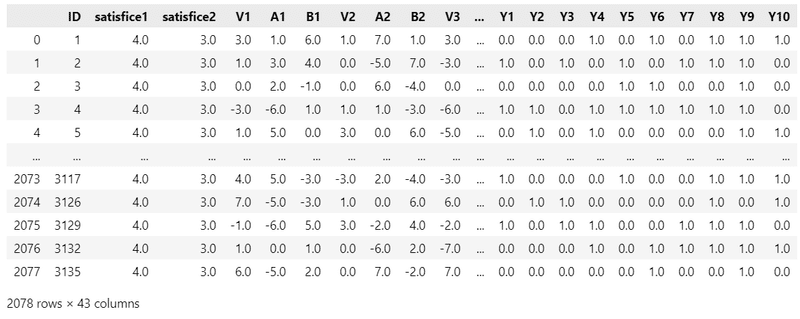
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み
data_orgn = pd.read_csv('song2018.csv')
display(data_orgn)

【実行結果】

３．データの前処理
Rスクリプトの掲載の前処理を実施します。

### データの前処理
data = data_orgn.copy()
# トラップ質問に正解したデータを抽出
data = data[(data['satisfice1']==4) & (data['satisfice2']==3)]
# 欠損値削除
data = data.dropna().reset_index(drop=True)
# データフレームの表示
display(data)

【実行結果】

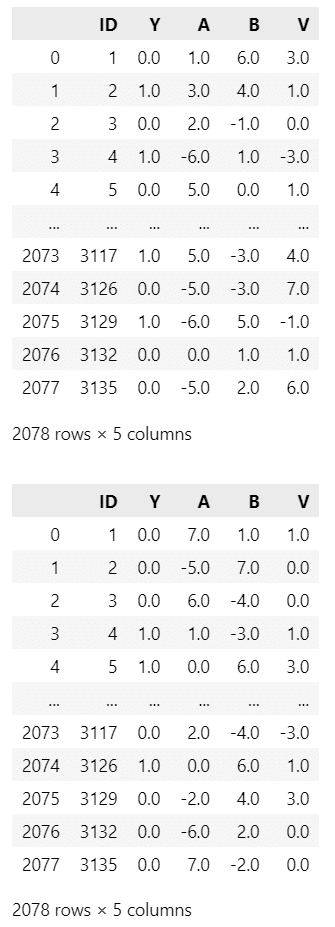
分析に用いる２つの争点を取り出します。

### ２つの争点データの作成
# 初期値設定：変更後列名
colnames = ['ID', 'Y', 'A', 'B', 'V']
# 争点1：憲法第9条
data1 = data[['ID', 'Y1', 'A1', 'B1', 'V1']]
data1.columns = colnames
display(data1)
# 争点2：市場vs国家
data2 = data[['ID', 'Y2', 'A2', 'B2', 'V2']]
data2.columns = colnames
display(data2)

【実行結果】
上段が争点「憲法９条改正」、下段が争点「市場vs国家」です。
変数は次のとおりです。
ID : 有権者（回答者）ID
Y : 投票結果（1: Aに投票, 0: Bに投票）
A : 候補者Ａの政策の位置（尺度）
B : 候補者Ｂの政策の（位置尺度）
V : 有権者の政策の位置（尺度）

４．データの概観の確認
箱ひげ図を描画してみます。
描画関数を作成します。

### 争点位置と投票先の関係の描画関数の定義
def plot_boxplot(df):
    df_plot = df.copy()
    df_plot.columns = ['ID', '投票先', '候補者A', '候補者B', '回答者V']
    df_plot = pd.melt(df_plot, id_vars=['ID', '投票先'],
                      value_vars=['候補者A', '候補者B', '回答者V'],
                      var_name='立場', value_name='争点位置')
    df_plot['投票先名'] = (df_plot['投票先']
                          .apply(lambda x: '候補者A' if x==1 else '候補者B'))
    sns.boxplot(data=df_plot, x='立場', y='争点位置', hue='投票先名',
                hue_order=['候補者A', '候補者B'], palette='Pastel1')
    plt.legend(ncol=2, bbox_to_anchor=(0.5, 1),loc='lower center',
               title='投票結果')
    plt.show()

憲法９条改正の描画です。

### 争点位置と投票先の関係の描画：争点１
plot_boxplot(data1)

【実行結果】
横軸に候補者と回答者（有権者）を並べて、縦軸に三者の争点位置（尺度）をプロットしました。
赤色が候補者Ａ投票分、青色が候補者Ｂ投票分です。

回答者の箱ひげ図の形状が面白いです。
候補者Ａに投票した回答者も、候補者Ｂに投票した回答者も、同じ形＝同じ争点位置の分布だとすると、候補者選びの決め手は何だったのでしょう？

続いて市場vs国家の描画です。

### 争点位置と投票先の関係の描画：争点２
plot_boxplot(data2)

【実行結果】

こちらの回答者（有権者）は争点位置のばらつきが小さい感じです。

ではではPyMCモデリングを実践いたしましょう。
３モデル$${\times}$$２争点＝６つのモデリングです。
長いですよーーーー。

近接性モデル　争点１

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\alpha &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=100) \\
\beta &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=100) \\
U_A &= -\text{abs}\ (V - A),\ \text{dims}=data \\
U_B &= -\text{abs}\ (V - B),\ \text{dims}=data \\
\theta &= \text{invlogit}\ (\alpha + \beta\ (U_A - U_B)),\ \text{dims}=data \\
likelihood &\sim \text{Bernoulli}\ (\text{p}=\theta,\ \text{dims}=data) \\
\end{align*}
$$

１．モデルの定義
数式表現を実直にモデル記述します。

### モデルの定義
with pm.Model() as model1_1:
    
    ### データ関連定義
    ## coordの定義
    model1_1.add_coord('data', values=data1.index, mutable=True)
    ## dataの定義
    # 投票先Y 1:候補者A、0:候補者B
    Y = pm.ConstantData('Y', value=data1['Y'].values, dims='data')
    # 回答者の争点位置V
    V = pm.ConstantData('V', value=data1['V'].values, dims='data')
    # 候補者Aの争点位置A
    A = pm.ConstantData('A', value=data1['A'].values, dims='data')
    # 候補者Bの争点位置B
    B = pm.ConstantData('B', value=data1['B'].values, dims='data')

    ### 事前分布
    # 切片α、傾きβ
    alpha = pm.Cauchy('alpha', alpha=0, beta=100)
    beta = pm.Cauchy('beta', alpha=0, beta=100)
    # 近接性モデル
    UA = pm.Deterministic('UA', -pt.abs(V - A), dims='data')
    UB = pm.Deterministic('UB', -pt.abs(V - B), dims='data')
    # 候補者Aを選択する確率θ
    theta = pm.Deterministic('theta', pm.invlogit(alpha + beta * (UA - UB)),
                             dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=theta, observed=Y, dims='data')

【モデル注釈】

coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の１つを設定しました。
- データの行の座標：名前「data」、値「行インデックス」
dataの定義
次の４つを設定しました。
- 投票結果：Y （目的変数）
- 回答者の争点位置：V
- 候補者Ａの争点位置：A
- 候補者Ｂの争点位置：B
パラメータの事前分布
- モデルの数式表現のとおりです。
尤度
- 二項分布です。

２．モデルの外観の確認

# モデルの表示
model1_1

【実行結果】

### モデルの可視化
pm.model_to_graphviz(model1_1)

【実行結果】

３．事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
後でWAICを計算するので、log_likelihood を算出します。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを未使用　30秒
# テキスト: iter=6000, warmup=1000, chains=4

# 乱数シードを日付（文字列）で設定
seed_date1_1 = '2019-03-03'
seed1_1 = int(pd.to_datetime(seed_date1_1).timestamp())

# サンプリング
with model1_1:
    idata1_1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                         nuts_sampler='numpyro', random_seed=seed1_1,
                         idata_kwargs={'log_likelihood': True},  # WAIC計算用
                         )

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。

### r_hat>1.1の確認
# 設定
idata_in = idata1_1      # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

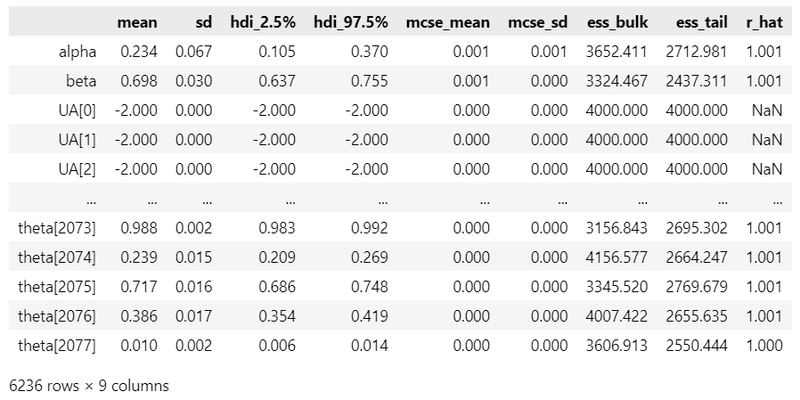
ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata1_1, hdi_prob=0.95, round_to=3)

【実行結果】
UAとUBはデータのV、A、Bから確定値を計算するので、rhatの値がNaNになっているのでしょう。

トレースプロットで事後分布サンプリングデータの様子を確認します。
theta は一部のパラメータのみの表示です。

### トレースプロットの表示
var_names = ['alpha', 'beta', 'theta']
pm.plot_trace(idata1_1, compact=False, var_names=var_names)
plt.tight_layout();

【実行結果】
左のグラフから、４本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

Yの事後予測サンプリングデータを取得します。

### 事後予測サンプリング
with model1_1:
    idata1_1.extend(pm.sample_posterior_predictive(idata1_1, random_seed=seed1_1))

【実行結果】省略

５．評価指標の算出
テキストにならって、的中率（accuracy）、$${\kappa}$$統計量、WAICの３つの評価指標を算出します。

まず評価指標算出関数を定義します。
scikit-learn を用いて的中率（accuracy_score）と$${\kappa}$$統計量（cohen_kappa_score）を算出し、arvizを用いてWAIC（waic）を算出します。

### 評価指標算出関数の定義 

def calc_metrics(df, idata, issue, model):
    # Yの事後予測データの取り出し
    y_post = (idata.posterior_predictive.likelihood
              .stack(sample=('chain', 'draw')).data)
    # Yの予測値の算出　事後予測の平均値>0.5 の時:1, それ以外の時:0
    y_pred = np.where(y_post.sum(axis=1)/y_post.shape[1] > 0.5, 1, 0)
    # 評価指標を算出しつつデータフレーム化
    metrics_df = pd.DataFrame({
                '争点': [issue],
                'モデル': [model],
                '的中率': [accuracy_score(df['Y'], y_pred)],
                'Kappa': [cohen_kappa_score(df['Y'], y_pred)],
                'WAIC': [az.waic(idata, scale='deviance')[0]]})
    # 戻り値：評価指標のデータフレーム
    return metrics_df

争点１の近接性モデルの評価指標を算出します。

### 評価指標の算出
metrics_df1_1 = calc_metrics(data1, idata1_1, '憲法第9条改正', '近接性モデル')
display(metrics_df1_1.round(3))

【実行結果】
これらの指標の数値は、後ほどモデル比較のときに活躍します。

６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata1_1をpickleで保存します。

### idataの保存 pickle
file = r'idata1_1_ch10.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata1_1, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata1_1_ch10.pkl'
with open(file, 'rb') as f:
    idata1_1_load = pickle.load(f)

近接性モデル　争点２

モデルの数式表現
争点１と同じです。

１．モデルの定義
争点１と同じです。利用データのみ変更します。

### モデルの定義
with pm.Model() as model1_2:
    
    ### データ関連定義
    ## coordの定義
    model1_2.add_coord('data', values=data2.index, mutable=True)
    ## dataの定義
    # 投票先Y 1:候補者A、0:候補者B
    Y = pm.ConstantData('Y', value=data2['Y'].values, dims='data')
    # 回答者の争点位置V
    V = pm.ConstantData('V', value=data2['V'].values, dims='data')
    # 候補者Aの争点位置A
    A = pm.ConstantData('A', value=data2['A'].values, dims='data')
    # 候補者Bの争点位置B
    B = pm.ConstantData('B', value=data2['B'].values, dims='data')

    ### 事前分布
    # 切片α、傾きβ
    alpha = pm.Cauchy('alpha', alpha=0, beta=100)
    beta = pm.Cauchy('beta', alpha=0, beta=100)
    # 近接性モデル
    UA = pm.Deterministic('UA', -pt.abs(V - A), dims='data')
    UB = pm.Deterministic('UB', -pt.abs(V - B), dims='data')
    # 候補者Aを選択する確率θ
    theta = pm.Deterministic('theta', pm.invlogit(alpha + beta * (UA - UB)),
                             dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=theta, observed=Y, dims='data')

【モデル注釈】省略

２．モデルの外観の確認

# モデルの表示
model1_2

【実行結果】

### モデルの可視化
pm.model_to_graphviz(model1_2)

【実行結果】

３．事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
後でWAICを計算するので、log_likelihood を算出します。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ10秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　10秒
# テキスト: iter=6000, warmup=1000, chains=4

# 乱数シードを日付（文字列）で設定
seed_date1_2 = '2019-03-04'
seed1_2 = int(pd.to_datetime(seed_date1_2).timestamp())

# サンプリング
with model1_2:
    idata1_2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                         nuts_sampler='numpyro', random_seed=seed1_2,
                         idata_kwargs={'log_likelihood': True},  # WAIC計算用
                         )

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata1_2      # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata1_2, hdi_prob=0.95, round_to=3)

【実行結果】
UAとUBはデータのV、A、Bから確定値を計算するので、rhatの値がNaNになっているのでしょう。

トレースプロットで事後分布サンプリングデータの様子を確認します。
theta は一部のパラメータのみの表示です。

### トレースプロットの表示
var_names = ['alpha', 'beta', 'theta']
pm.plot_trace(idata1_2, compact=False, var_names=var_names)
plt.tight_layout();

Yの事後予測サンプリングデータを取得します。

### 事後予測サンプリング
with model1_2:
    idata1_2.extend(pm.sample_posterior_predictive(idata1_2, random_seed=seed1_2))

【実行結果】省略

５．評価指標の算出
テキストにならって、的中率（accuracy）、$${\kappa}$$統計量、WAICの３つの評価指標を算出します。
争点２の近接性モデルの評価指標を算出します。

### 評価指標の算出
metrics_df1_2 = calc_metrics(data2, idata1_2, '市場vs国家', '近接性モデル')
display(metrics_df1_2.round(3))

【実行結果】
これらの指標の数値は、後ほどモデル比較のときに活躍します。

６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata1_2をpickleで保存します。

### idataの保存 pickle
file = r'idata1_2_ch10.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata1_2, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata1_2_ch10.pkl'
with open(file, 'rb') as f:
    idata1_2_load = pickle.load(f)

方向性モデル　争点１

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
UAとUB以外は近接性モデルとまったく同じです。

$$
\begin{align*}
\alpha &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=100) \\
\beta &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=100) \\
U_A &= V \times A,\ \text{dims}=data \\
U_B &= V \times A,\ \text{dims}=data \\
\theta &= \text{invlogit}\ (\alpha + \beta\ (U_A - U_B)),\ \text{dims}=data \\
likelihood &\sim \text{Bernoulli}\ (\text{p}=\theta,\ \text{dims}=data) \\
\end{align*}
$$

１．モデルの定義
数式表現を実直にモデル記述します。

### モデルの定義
with pm.Model() as model2_1:
    
    ### データ関連定義
    ## coordの定義
    model2_1.add_coord('data', values=data1.index, mutable=True)
    ## dataの定義
    # 投票先Y 1:候補者A、0:候補者B
    Y = pm.ConstantData('Y', value=data1['Y'].values, dims='data')
    # 回答者の争点位置V
    V = pm.ConstantData('V', value=data1['V'].values, dims='data')
    # 候補者Aの争点位置A
    A = pm.ConstantData('A', value=data1['A'].values, dims='data')
    # 候補者Bの争点位置B
    B = pm.ConstantData('B', value=data1['B'].values, dims='data')

    ### 事前分布
    # 切片α、傾きβ
    alpha = pm.Cauchy('alpha', alpha=0, beta=100)
    beta = pm.Cauchy('beta', alpha=0, beta=100)
    # 方向性モデル
    UA = pm.Deterministic('UA', V * A, dims='data')
    UB = pm.Deterministic('UB', V * B, dims='data')
    # 候補者Aを選択する確率θ
    theta = pm.Deterministic('theta', pm.invlogit(alpha + beta * (UA - UB)),
                             dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=theta, observed=Y, dims='data')

【モデル注釈】省略（近接性モデルと同様です）

２．モデルの外観の確認

# モデルの表示
model2_1

【実行結果】
UAとUBの式の中身が表示されないせいか、近接性モデルと全く同じ表示になっています。

### モデルの可視化
pm.model_to_graphviz(model2_1)

【実行結果】
この図も近接性モデルと全く同じ表示になっています。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　10秒
# テキスト: iter=6000, warmup=1000, chains=4

# 乱数シードを日付（文字列）で設定
seed_date2_1 = '2019-03-10'
seed2_1 = int(pd.to_datetime(seed_date2_1).timestamp())

# サンプリング
with model2_1:
    idata2_1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                         nuts_sampler='numpyro', random_seed=seed2_1,
                         idata_kwargs={'log_likelihood': True},  # WAIC計算用
                         )

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata2_1      # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata2_1, hdi_prob=0.95, round_to=3)

【実行結果】
UAとUBはデータのV、A、Bから確定値を計算するので、rhatの値がNaNになっているのでしょう。

トレースプロットで事後分布サンプリングデータの様子を確認します。
theta は一部のパラメータのみの表示です。

### トレースプロットの表示
var_names = ['alpha', 'beta', 'theta']
pm.plot_trace(idata2_1, compact=False, var_names=var_names)
plt.tight_layout();

Yの事後予測サンプリングデータを取得します。

### 事後予測サンプリング
with model2_1:
    idata2_1.extend(pm.sample_posterior_predictive(idata2_1, random_seed=seed2_1))

【実行結果】省略

５．評価指標の算出
テキストにならって、的中率（accuracy）、$${\kappa}$$統計量、WAICの３つの評価指標を算出します。

争点１の方向性モデルの評価指標を算出します。

### 評価指標の算出
metrics_df2_1 = calc_metrics(data1, idata2_1, '憲法第9条改正', '方向性モデル')
display(metrics_df2_1.round(3))

【実行結果】
これらの指標の数値は、後ほどモデル比較のときに活躍します。

６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata2_1をpickleで保存します。

### idataの保存 pickle
file = r'idata2_1_ch10.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata2_1, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata2_1_ch10.pkl'
with open(file, 'rb') as f:
    idata2_1_load = pickle.load(f)

方向性モデル　争点２

モデルの数式表現
争点１と同じです。

１．モデルの定義
争点１と同じです。利用データのみ変更します。

### モデルの定義
with pm.Model() as model2_2:
    
    ### データ関連定義
    ## coordの定義
    model2_2.add_coord('data', values=data2.index, mutable=True)
    ## dataの定義
    # 投票先Y 1:候補者A、0:候補者B
    Y = pm.ConstantData('Y', value=data2['Y'].values, dims='data')
    # 回答者の争点位置V
    V = pm.ConstantData('V', value=data2['V'].values, dims='data')
    # 候補者Aの争点位置A
    A = pm.ConstantData('A', value=data2['A'].values, dims='data')
    # 候補者Bの争点位置B
    B = pm.ConstantData('B', value=data2['B'].values, dims='data')

    ### 事前分布
    # 切片α、傾きβ
    alpha = pm.Cauchy('alpha', alpha=0, beta=100)
    beta = pm.Cauchy('beta', alpha=0, beta=100)
    # 方向性モデル
    UA = pm.Deterministic('UA', V * A, dims='data')
    UB = pm.Deterministic('UB', V * B, dims='data')
    # 候補者Aを選択する確率θ
    theta = pm.Deterministic('theta', pm.invlogit(alpha + beta * (UA - UB)),
                             dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=theta, observed=Y, dims='data')

【モデル注釈】省略

２．モデルの外観の確認

# モデルの表示
model2_2

【実行結果】
UAとUBの式の中身が表示されないせいか、近接性モデルと全く同じ表示になっています。

### モデルの可視化
pm.model_to_graphviz(model1_2)

【実行結果】
この図も近接性モデルと全く同じ表示になっています。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　10秒
# テキスト: iter=6000, warmup=1000, chains=4

# 乱数シードを日付（文字列）で設定
seed_date2_2 = '2019-03-11'
seed2_2 = int(pd.to_datetime(seed_date2_2).timestamp())

# サンプリング
with model2_2:
    idata2_2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                         nuts_sampler='numpyro', random_seed=seed2_2,
                         idata_kwargs={'log_likelihood': True},  # WAIC計算用
                         )

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata2_2      # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata2_2, hdi_prob=0.95, round_to=3)

【実行結果】
UAとUBはデータのV、A、Bから確定値を計算するので、rhatの値がNaNになっているのでしょう。

トレースプロットで事後分布サンプリングデータの様子を確認します。
theta は一部のパラメータのみの表示です。

### トレースプロットの表示
var_names = ['alpha', 'beta', 'theta']
pm.plot_trace(idata2_2, compact=False, var_names=var_names)
plt.tight_layout();

Yの事後予測サンプリングデータを取得します。

### 事後予測サンプリング
with model2_2:
    idata2_2.extend(pm.sample_posterior_predictive(idata2_2, random_seed=seed2_2))

【実行結果】省略

５．評価指標の算出
テキストにならって、的中率（accuracy）、$${\kappa}$$統計量、WAICの３つの評価指標を算出します。
争点２の近接モデルの評価指標を算出します。

### 評価指標の算出
metrics_df2_2 = calc_metrics(data2, idata2_2, '市場vs国家', '方向性モデル')
display(metrics_df2_2.round(3))

【実行結果】
これらの指標の数値は、後ほどモデル比較のときに活躍します。

６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata2_2をpickleで保存します。

### idataの保存 pickle
file = r'idata2_2_ch10.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata2_2, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata2_2_ch10.pkl'
with open(file, 'rb') as f:
    idata2_2_load = pickle.load(f)

伸縮近接性モデル　争点１

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
UAとUB以外は近接性モデル・方向性モデルとまったく同じです。

$$
\begin{align*}
\alpha &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=100) \\
\beta &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=100) \\
U_A &= -\text{abs}\ (\text{ev}\ (V,\ \omega) - \text{ev}\ (A,\ \omega) ),\ \text{dims}=data \\
U_B &= -\text{abs}\ (\text{ev}\ (V,\ \omega) - \text{ev}\ (B,\ \omega) ),\ \text{dims}=data \\
\theta &= \text{invlogit}\ (\alpha + \beta\ (U_A - U_B)),\ \text{dims}=data \\
likelihood &\sim \text{Bernoulli}\ (\text{p}=\theta,\ \text{dims}=data) \\
\end{align*}
$$

$${U_A,\ U_B}$$の式に出現した謎の関数$${\text{ev()}}$$。
この関数は$${\tilde{V_i},\ \tilde{P_k}}$$を算出する自作関数ですテヘ

### 「期待値x_hat = sign x * Σ_{s=0}^{x-1} ω^s 」を計算する関数の定義
# 引数
#  x     : pytensor変数V, A, B
#  omega : パラメータω 

def ev(x, omega):

    # 変数xの絶対値の算出
    absx = pt.abs(x)
    
    # パラメータomegaの指数の総和計算（全パターン）：sum_{s=0}^{absx-1}(omega**s)
    sumOmega0 = pt.pow(omega, 0)
    sumOmega1 = pt.pow(omega, 1) + sumOmega0
    sumOmega2 = pt.pow(omega, 2) + sumOmega1
    sumOmega3 = pt.pow(omega, 3) + sumOmega2
    sumOmega4 = pt.pow(omega, 4) + sumOmega3
    sumOmega5 = pt.pow(omega, 5) + sumOmega4
    sumOmega6 = pt.pow(omega, 6) + sumOmega5
    
    # 変数xの絶対値の値に応じてパラメータomegaの指数の総和を選択
    sumOmegaPows = pt.switch(pt.eq(absx, 0), 0,
                   pt.switch(pt.eq(absx, 1), sumOmega0,
                   pt.switch(pt.eq(absx, 2), sumOmega1,
                   pt.switch(pt.eq(absx, 3), sumOmega2,
                   pt.switch(pt.eq(absx, 4), sumOmega3,
                   pt.switch(pt.eq(absx, 5), sumOmega4,
                   pt.switch(pt.eq(absx, 6), sumOmega5,
                   pt.switch(pt.eq(absx, 7), sumOmega6, 0))))))))

    # 変数xのプラスマイナスの符号の算出
    sign = pt.switch(pt.gt(x, 0), 1, -1)
    
    # 戻り値：符号 × omegaの指数の総和
    return sign * sumOmegaPows

１．モデルの定義
数式表現を実直にモデル記述します。

### モデルの定義
with pm.Model() as model3_1:
    
    ### データ関連定義
    ## coordの定義
    model3_1.add_coord('data', values=data1.index, mutable=True)
    ## dataの定義
    # 投票先Y 1:候補者A、0:候補者B
    Y = pm.ConstantData('Y', value=data1['Y'].values, dims='data')
    # 回答者の争点位置V
    V = pm.ConstantData('V', value=data1['V'].values, dims='data')
    # 候補者Aの争点位置A
    A = pm.ConstantData('A', value=data1['A'].values, dims='data')
    # 候補者Bの争点位置B
    B = pm.ConstantData('B', value=data1['B'].values, dims='data')

    ### 事前分布
    # 切片α、傾きβ、距離の縮み具合ω
    alpha = pm.Cauchy('alpha', alpha=0, beta=100)
    beta = pm.Cauchy('beta', alpha=0, beta=100)
    omega = pm.Uniform('omega', lower=0, upper=2)
    # 方向性モデル
    UA = pm.Deterministic('UA', -pt.abs(ev(V, omega) - ev(A, omega)),
                          dims='data')
    UB = pm.Deterministic('UB', -pt.abs(ev(V, omega) - ev(B, omega)),
                          dims='data')
    # 候補者Aを選択する確率θ
    theta = pm.Deterministic('theta', pm.invlogit(alpha + beta * (UA - UB)),
                             dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=theta, observed=Y, dims='data')

【モデル注釈】省略（近接性モデルと同様です）

２．モデルの外観の確認

# モデルの表示
model3_1

【実行結果】
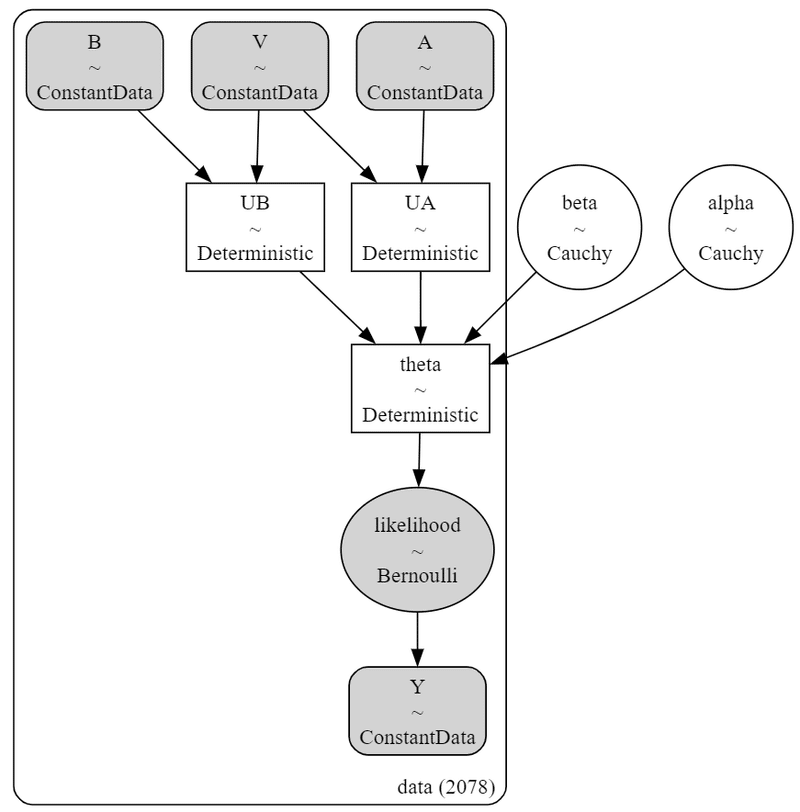
omega の登場です。

### モデルの可視化
pm.model_to_graphviz(model3_1)

【実行結果】
この図も近接性モデルと全く同じ表示になっています。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　30秒
# テキスト: iter=6000, warmup=1000, chains=4

# 乱数シードを日付（文字列）で設定
seed_date3_1 = '2019-03-20'
seed3_1 = int(pd.to_datetime(seed_date3_1).timestamp())

# サンプリング
with model3_1:
    idata3_1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                         nuts_sampler='numpyro', random_seed=seed3_1,
                         idata_kwargs={'log_likelihood': True},  # WAIC計算用
                         )

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata3_1      # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
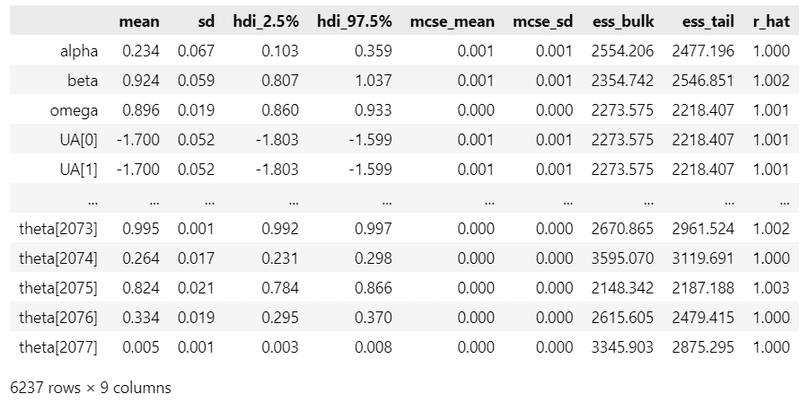
pm.summary(idata3_1, hdi_prob=0.95, round_to=3)

【実行結果】
UAとUBは確率変数omegaの出現で確率的に動くようになりました。

トレースプロットで事後分布サンプリングデータの様子を確認します。
theta は一部のパラメータのみの表示です。

### トレースプロットの表示
var_names = ['alpha', 'beta', 'omega', 'theta']
pm.plot_trace(idata3_1, compact=False, var_names=var_names)
plt.tight_layout();

Yの事後予測サンプリングデータを取得します。

### 事後予測サンプリング
with model3_1:
    idata3_1.extend(pm.sample_posterior_predictive(idata3_1, random_seed=seed3_1))

【実行結果】省略

５．評価指標の算出
テキストにならって、的中率（accuracy）、$${\kappa}$$統計量、WAICの３つの評価指標を算出します。

争点１の方向性モデルの評価指標を算出します。

### 評価指標の算出
metrics_df3_1 = calc_metrics(data1, idata3_1, '憲法第9条改正', '伸縮近接性モデル')
display(metrics_df3_1.round(3))

【実行結果】
これらの指標の数値は、後ほどモデル比較のときに活躍します。

６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata3_1をpickleで保存します。

### idataの保存 pickle
file = r'idata3_1_ch10.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata3_1, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata3_1_ch10.pkl'
with open(file, 'rb') as f:
    idata3_1_load = pickle.load(f)

伸縮近接性モデル　争点２

さあ、最後のモデリングです！

モデルの数式表現
争点１と同じです。

１．モデルの定義
争点１と同じです。利用データのみ変更します。

### モデルの定義

with pm.Model() as model3_2:

    ### データ関連定義
    ## coordの定義
    model3_2.add_coord('data', values=data2.index, mutable=True)
    ## dataの定義
    # 投票先Y 1:候補者A、0:候補者B
    Y = pm.ConstantData('Y', value=data2['Y'].values, dims='data')
    # 回答者の争点位置V
    V = pm.ConstantData('V', value=data2['V'].values, dims='data')
    # 候補者Aの争点位置A
    A = pm.ConstantData('A', value=data2['A'].values, dims='data')
    # 候補者Bの争点位置B
    B = pm.ConstantData('B', value=data2['B'].values, dims='data')

    ### 事前分布
    # 切片α、傾きβ、距離の縮み具合ω
    alpha = pm.Cauchy('alpha', alpha=0, beta=100)
    beta = pm.Cauchy('beta', alpha=0, beta=100)
    omega = pm.Uniform('omega', lower=0, upper=2)
    # 方向性モデル
    UA = pm.Deterministic('UA', -pt.abs(ev(V, omega) - ev(A, omega)),
                          dims='data')
    UB = pm.Deterministic('UB', -pt.abs(ev(V, omega) - ev(B, omega)),
                          dims='data')
    # 候補者Aを選択する確率θ
    theta = pm.Deterministic('theta', pm.invlogit(alpha + beta * (UA - UB)),
                             dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=theta, observed=Y, dims='data')

【モデル注釈】省略

２．モデルの外観の確認

# モデルの表示
model3_2

【実行結果】

### モデルの可視化
pm.model_to_graphviz(model3_2)

【実行結果】
この図も近接性モデルと全く同じ表示になっています。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　30秒
# テキスト: iter=6000, warmup=1000, chains=4

# 乱数シードを日付（文字列）で設定
seed_date3_2 = '2019-03-21'
seed3_2 = int(pd.to_datetime(seed_date3_2).timestamp())

# サンプリング
with model3_2:
    idata3_2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                         nuts_sampler='numpyro', random_seed=seed3_2,
                         idata_kwargs={'log_likelihood': True},  # WAIC計算用
                         )

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata3_2      # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R} > 1.01}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata3_2, hdi_prob=0.95, round_to=3)

【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
theta は一部のパラメータのみの表示です。

### トレースプロットの表示
var_names = ['alpha', 'beta', 'omega', 'theta']
pm.plot_trace(idata3_2, compact=False, var_names=var_names)
plt.tight_layout();

Yの事後予測サンプリングデータを取得します。

### 事後予測サンプリング
with model3_2:
    idata3_2.extend(pm.sample_posterior_predictive(idata3_2, random_seed=seed3_2))

【実行結果】省略

### 評価指標の算出
metrics_df3_2 = calc_metrics(data2, idata3_2, '市場vs国家', '伸縮近接性モデル')
display(metrics_df3_2.round(3))

【実行結果】
これらの指標の数値は、後ほどモデル比較のときに活躍します。

６．推論データの保存
推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idata3_2をpickleで保存します。

### idataの保存 pickle
file = r'idata3_2_ch10.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata3_2, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata3_2_ch10.pkl'
with open(file, 'rb') as f:
    idata3_2_load = pickle.load(f)

分析

１．３つのモデルの比較

２つの争点について３つのモデルを比較します。
テキストの表10.1に相当します。

### ３つの争点投票モデルの比較 ※表10.1に相当
comp_df = pd.concat([metrics_df1_1, metrics_df2_1, metrics_df3_1,
                     metrics_df1_2, metrics_df2_2, metrics_df3_2], axis=0)
display(comp_df.round(3))

【実行結果】

【分析～テキストにならって】
争点１については、的中率（値が大きいほど当てはまりがよい）、$${\kappa}$$統計量（１に近いほど当てはまりがよい）、WAIC（値が小さいほど当てはまりがよい）の全てで「伸縮近接性モデル」の当てはまりがよいとの結果です
争点２については、「近接性モデル」と「伸縮近接性モデル」がほぼ同じ程度で当てはまりがよいとの結果です。

テキストは、２つの争点の結果を合わせて「伸縮近接性モデル」の当てはまりが最もよいと言えそうだ、としています。

２．伸縮近接性モデルのパラメータの確認

テキストは、上記の当てはまりの流れを受けて、伸縮近接性モデルのパラメータの推定値を確認します。
テキストの表10.2に相当します。

### 伸縮近接性モデルによる推定結果 ※表10.2に相当

# 事後分布統計量算出関数の定義（戻り値：データフレーム）
def calc_stats(idata, issue, param):
    samples = idata.posterior[param].data.flatten()
    hdi = az.hdi(samples)
    return pd.DataFrame([issue, param, np.mean(samples), np.median(samples),
                         np.std(samples), hdi[0], hdi[1]]).T

# 初期値設定
issues = ['憲法9条改正', '市場vs国家']
cols = ['争点', 'パラメータ', 'EAP', 'MED', 'SD', 'HDI2.5%', 'HDI97.5%']

# 事後統計量のデータフレームの作成
stats_df = pd.concat([calc_stats(idata3_1, issues[0], 'alpha'),
                      calc_stats(idata3_1, issues[0], 'beta'),
                      calc_stats(idata3_1, issues[0], 'omega'),
                      calc_stats(idata3_2, issues[1], 'alpha'),
                      calc_stats(idata3_2, issues[1], 'beta'),
                      calc_stats(idata3_2, issues[1], 'omega'),
                     ], axis=0
                     ).set_axis(cols, axis='columns').reset_index(drop=True)
# 数値型の変更
stats_df = stats_df.astype({'EAP': 'float64', 'MED': 'float64', 'SD': 'float64',
                            'HDI2.5%': 'float64', 'HDI97.5%': 'float64'})

# データフレームの表示
display(stats_df.round(3))

【実行結果】

効用の差$${U_A-U_B}$$にかかる係数$${\beta}$$に注目します。
テキストは係数$${\beta}$$を「政策の位置（尺度）の違いが特定の候補者に対する投票確率に与える影響」としています。
候補者の政策位置が有権者の候補者選択に影響を与えているかどうかを検討します。

【分析～テキストにならって】
争点１の$${\beta}$$の推定値は95%HDI$${[0.81,\ 1.03]}$$であり、0をまたがない正の値です。
このことは、候補者・政党の政策位置の違いが有権者による候補者選択行動に影響を与えている、と考えることができそうです。
争点２の$${\beta}$$の推定値95%HDI$${[0.56,\ 0.72]}$$も同様に、候補者・政党の政策位置の違いが有権者による候補者選択行動に影響を与えている、と考えることができそうです。

３．伸縮近接性モデルによる政策空間の伸縮

政策空間の伸縮度を表すパラメータ$${\omega}$$に注目します。
テキスト図10.2の争点ごとの$${\omega}$$の事後分布を描画します。

### ωの事後分布の比較 ※図10.2に相当

# 描画領域の指定
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(7, 5), sharex=True)

# 憲法9条改正のωの事後分布の描画
pm.plot_posterior(idata3_1.posterior.omega, hdi_prob=0.95, round_to=3,
                  ref_val=1, color='tab:blue', ax=ax1)
ax1.set(xlim=[0.78, 1.23], title='憲法9条改正', xlabel='ω', ylabel='確率密度')
ax1.grid(lw=0.5)

# 市場vs国家のωの事後分布の描画
pm.plot_posterior(idata3_2.posterior.omega, hdi_prob=0.95, round_to=3,
                  ref_val=1, color='tab:red', ax=ax2)
ax2.set(title='市場vs国家', xlabel='ω', ylabel='確率密度')
ax2.grid(lw=0.5)

plt.tight_layout()
plt.show()

【実行結果】

テキストによると$${\omega}$$の値によって以下のことが言えるそうです。
・$${\omega<1}$$：政策空間は縮んでいる
・$${\omega>1}$$：政策空間は拡大している
・$${\omega=1}$$：近接モデルに一致する

【分析～テキストにならって】
争点１の$${\omega}$$の推定値は95%HDI$${[0.86,\ 0.93]}$$であり、また、１未満の確率が100％です。
つまり、政策空間は縮んでいると考えられます。
争点２の$${\omega}$$の推定値は95%HDI$${[0.97,\ 1.05]}$$であり、1をまたいでいます。また、１未満の確率が22％です。
この結果は、政策空間が縮んでいるとも拡大しているとも言えないです。

４．近接性モデルと伸縮近接性モデルの効用差

効用の差$${U_A-U_B}$$について、横軸：近接性モデル・縦軸：伸縮近接性のプロットを描画します。
テキストの図10.3に相当します。

### ２つの争点投票モデルにおけるUAとUBの差の描画 ※図10.3に相当

# for文で回しやすいようにリスト化
dfs = [data1, data2]                    # 観測値のデータフレーム
idatas = [idata3_1, idata3_2]           # 推論データ 
titles = ['憲法9条改正', '市場vs国家']   # 争点名称

# 描画領域の指定
fig, ax = plt.subplots(1, 2, figsize=(8.5, 4))

# ２回繰り返し処理
for i, (df, idata, title) in enumerate(zip(dfs, idatas, titles)): 
    ### データ加工
    ## 観測データから近接性モデルのUA-UBを算出
    diff_proximity = (-abs(df['V'] - df['A']) + abs(df['V'] - df['B'])).values
    ## 事後分布データから伸縮近接性モデルのUA-UB（中央値）を算出
    # 推論データからUA,UBを取り出し shape=(データ点2078, MCMCサンプル4000)
    UA = idata.posterior.UA.stack(sample=('chain', 'draw')).data
    UB = idata.posterior.UB.stack(sample=('chain', 'draw')).data
    # UAとUBの差を算出 shape=(データ点2078, MCMCサンプル4000)
    diff_elastic = UA - UB
    # 差の中央値の算出 shape=(データ点2078)
    diff_elastic_median = np.median(diff_elastic, axis=1)
    
    ### 描画
    # 散布図の描画　x軸：近接性モデルの差、y軸：伸縮近接性モデルの差
    ax[i].scatter(diff_proximity, diff_elastic_median, alpha=0.3)
    # 45度線の描画
    ax[i].plot([-15, 15], [-15, 15], color='tomato')
    # 修飾
    ax[i].set(xlabel='近接性モデル', ylabel='伸縮拡張性モデル', title=title,
              xticks=range(-15, 16, 5), aspect='equal')
    ax[i].grid(lw=0.5)

plt.tight_layout()
plt.show()

【実行結果】

【分析～テキストにならって】
争点１（左）は横軸の両端に近づくほど、近接性モデルに比べて伸縮近接性モデルの効用差が小さくなっています。
伸縮近接性モデルにおける政策空間の縮みを反映しているようです。
一方で争点２（右）は横軸の両端においてもほぼ４５度線上に乗っています。
伸縮近接性モデルにおける政策空間の伸縮が見られず、政策空間上の距離そのものが効用差に影響を及ぼしているようです。

以上で第10章は終了です。

おわりに

選挙と政策

テキストが用いた調査データは、２つの政策を示されてどちらかを「必ず選ばなければならない」状況、つまり、「２つの政策情報を明確に与えられて、かつ、仕組み上、投票が義務付けられている」状況のように感じました。
実際の選挙のとき、みなさんはどのように候補者や政党を選んで投票していますか？
政策情報を把握して政策で選んでいますか？
それ以前に投票していますか？

総務省のサイトによると、2021年の衆院選投票率は55.93％。
半数近い有権者が投票していないようです。

政策に関しては、複数の政策争点・論点があったとして、すべてが自分の考えと一致する政党を見つけることができません。。。
過去にはマニフェストの用語が飛び交ったことがありましたが、うまく機能することができなかったようです。
また過去には１つの省庁の民営化を劇場型で展開して自由化を争点にした選挙もありました。ただ、バブル経済崩壊の後遺症と自由化が重なって、失われた◯◯年の不幸な延長をもたらしたように思えます。

候補者と有権者が政策論点を共有して、日本（の将来を）をよくする道筋を議論し、最適な政治代理人を選ぶことは、簡単なことでは無さそうです。

おわり

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

この記事が参加している募集

新生活をたのしく

37,076件

仕事のコツ

with 日本経済新聞

書いてみる

この記事が気に入ったらサポートをしてみませんか？

第10章「え！そっちに入れるんですか？」のベイズモデリングをPyMC Ver.5 で

サマリー

テキストの概要

自己評価

モデルの概要

テキストの調査・実験の概要

テキストのモデリング

PyMC実装

準備・データ確認

近接性モデル 争点１

近接性モデル 争点２

方向性モデル 争点１

方向性モデル 争点２

伸縮近接性モデル 争点１

伸縮近接性モデル 争点２

分析

おわりに

選挙と政策

シリーズの記事

ブログの紹介

この記事が参加している募集

近接性モデル　争点１

近接性モデル　争点２

方向性モデル　争点１

方向性モデル　争点２

伸縮近接性モデル　争点１

伸縮近接性モデル　争点２