
第14章「いつになったら原稿を書くのか?」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第14章「いつになったら原稿を書くのか?」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、遅筆に悩む著者が7つの原稿の「毎日の執筆量データ」をコード化して蓄積、いつから執筆量が加速したのかを「変化点検出モデル」で推論しています。

今回は「テキストと異なるモデル」を作成して、7つの原稿の推論に取り組み、半数程度についてテキストに近い推論結果を得ることができました!
果たして著者のやる気スイッチはいつONになるのでしょう?
PyMCでモデリングして、ベイズを楽しみましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 国里愛彦 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★・・& そこそこ \\
結果再現度 & ★★★・・& そこそこ \\
楽しさ & ★★★★★& 楽しい! \\
\end{array}
$$

評価ポイント
テキストの変化点(執筆開始日からの経過日数)と合致するかどうかを評価の軸に置くと、合致率は4/7、つまり半数以上の原稿が合致しました。
ただし、合致しなかった原稿3つのうち、2つは収束できませんでした。
工夫・喜び・反省
離散値をパラメータに持てないStanでは「周辺化消去」という手法で対処するのですが、PyMCは離散値を扱えるのでStanと異なるモデルを構築できます。
今回は離散値のパラメータをモデルに取り込みました。
理由はPyMCによる「周辺化消去」の方法が分からないからです。
いつか周辺化消去(確率の和を取る)の方法をマスターしたいです。

モデルの概要
テキストの調査・実験の概要
■執筆量モニタリングと変化点
論文や原稿の執筆が進まない派の著者は、以下の書籍を読んだそうです。
要点は2つ。
・執筆スケジュールの作成と遵守
・執筆量のモニタリング
著者の凄いところは、執筆量管理をオートメーション化したこと。
Googleドキュメントで執筆すると、Google Apps ScriptでGoogleスプレッドシートに執筆量が自動記録され、さらに自動で進捗状況をメール通知する仕組みだそうです。
詳しい手法は、こちらの著者のサイトでご確認下さい。
これだけ気合いの入った執筆量の見える化と予実管理を徹底すれば、執筆開始当初からものすごいペースで執筆が進むことでしょう、と期待してしまいますが、「事実は小説よりも奇なり」ということもあり得ます(わくわく)。

■実験の概要
著者ご自身の原稿作成作業による「7つの原稿の執筆量データ」がベイズモデリングの主役です。
著者に「データは、時として残酷である」と言わしめた、あのデータです。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数$${text_{day}}$$は日々の累積執筆量(文字数)です。
最も関心のあるパラメータは、執筆量が加速した変化点(日数)である$${cp}$$です。
■モデル
1つ目の数式(というかプログラミングコード)は「変化点前」の累計執筆量、2つ目の数式は「変化点後」の累積執筆量をそれぞれ示しています。
いずれも1日前の累積執筆量に$${\mu_1}$$(変化点前の1日あたり執筆量)または$${\mu_2}$$(変化点後の1日あたり執筆量)を加算した量を平均パラメータとする正規分布に従うモデルです。
if day $${\leq}$$ cp
text [day] $${\sim}$$ Normal ( text [day - 1] + $${\mu_1}$$, $${\sigma}$$)
else
text [day] $${\sim}$$ Normal ( text [day - 1] + $${\mu_2}$$, $${\sigma}$$)
Stanによる実装では、整数値という離散値をとる変化点$${cp}$$をパラメータで直接推定できないとのことで、周辺化消去という手法を用いて、変化点$${cp}$$を推定しています。
周辺化消去手法に関してあまり詳しくないので、この記事では触れないようにします。
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCモデリングでの分析結果は、「PyMC実装」章の【5.分析】の部分をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
# データの読み込み
data = pd.read_csv('data.csv')
# データの表示
display(data)【実行結果】
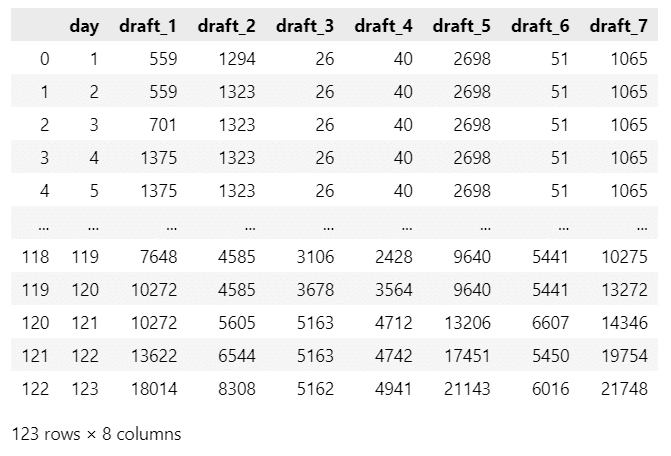
全123行、8列です。
データ項目は次のとおりです。
day:執筆経過日数(1~123日)
draft_1~draft_7:原稿1~原稿7の経過日数時点の累積執筆量(文字数)
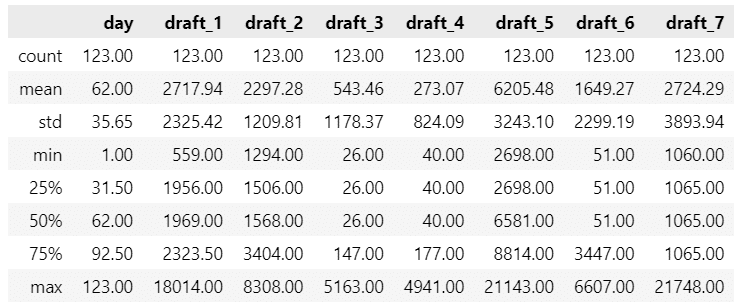
3.データの外観・統計量
ひとまず要約統計量を確認します。
### 要約統計量の表示
data.describe().round(2)【実行結果】
75%の日数が経過したとき、ほとんどの原稿は完成時の50%にも達していません(モニタリングとは?)。
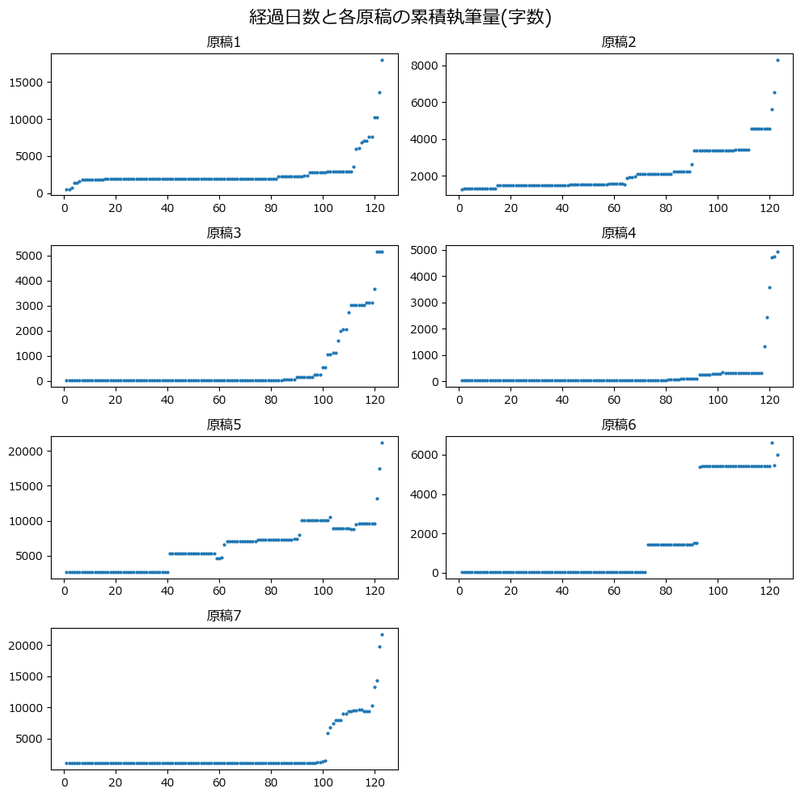
テキストにならって、経過日数ごとの累積執筆量のグラフを描画しましょう。
テキストの図14.2に相当します。
### 各原稿の執筆状況 ★図14.2に対応
plt.figure(figsize=(10, 10))
# 原稿1~7まで繰り返し処理
for i, col in enumerate(data.columns[1:]):
# サブプロットの作成
ax = plt.subplot(4, 2, i+1)
# 点グラフの描画
ax.plot(data['day'], data[col], 'o', markersize=2)
# タイトル(原稿n)の表示
ax.set_title(f'原稿{i+1}')
# 修飾
plt.suptitle('経過日数と各原稿の累積執筆量(字数)', fontsize=16)
plt.tight_layout()
plt.show()【実行結果】
こ、これは・・・(予実管理とは?)。
逆に言うと、10日あれば余裕で書ける体質なのでは!?
4.変化点検出モデルのシミュレーション
テキストにならって、変化点検出モデルのシミュレーションを行います。
テキストの図14.3に相当します。
乱数シードがテキストと異なるため、シミュレーションの結果はテキストと相違しています。
### 変化点検出モデルのシミュレーション ★図14.3に相当
# 設定
days, cp = 31, 23 # 日数、変化点
mu1, mu2, sigma = 50, 400, 30 # 変化点前の平均、変化点後の平均、標準偏差
# 初期値
text = np.zeros(days)
np.random.seed(123)
# シミュレーションの実施
for i in range(days):
if i==0:
text[i] = np.random.normal(loc=mu1, scale=sigma, size=1)
elif i <= cp-1:
text[i] = np.random.normal(loc=text[i-1] + mu1, scale=sigma, size=1)
else:
text[i] = np.random.normal(loc=text[i-1] + mu2, scale=sigma, size=1)
# 描画
plt.figure(figsize=(5, 4))
plt.plot(range(1, days+1), text, 'o-', markersize=4)
plt.axvline(cp, color='black', lw=0.8, ls='--')
plt.xlabel('日数')
plt.ylabel('累積執筆量(字数)')
plt.grid(lw=0.3)
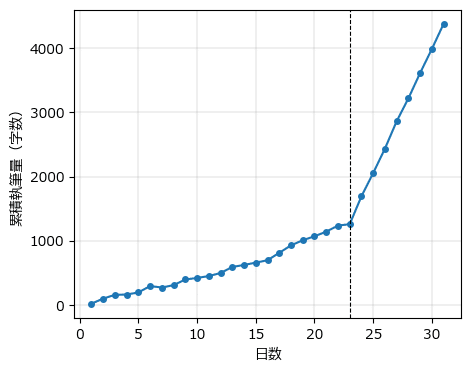
plt.show();【実行結果】
変化点$${cp}$$である23日以後、執筆が加速している感じが伝わります。
PyMCで取り組むモデルはまさに、このグラフのような変化点を探求するものです!
モデル構築
モデルの数式表現
PyMCのMCMCは離散パラメータに対応できます。
そこでこの記事では、変化点$${cp}$$が離散一様分布 DiscreteUniform に従うモデルを用います。
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\mu_1 &\sim \text{Uniform}\ (\text{lower}=-100000,\ \text{upper}=100000) \\
\mu_2 &\sim \text{Uniform}\ (\text{lower}=-100000,\ \text{upper}=100000) \\ \sigma &\sim \text{HalfCaushy}\ (\text{beta}=100) \\
cp &\sim \text{DiscreteUniform}\ (\text{lower}=1,\ \text{upper}=123) \\
\text{if}\ &dayIdx==0: \\
&\quad \mu = \mu_1 \\
\text{elif}\ &dayIdx \leq cp-1: \\
&\quad \mu = text_{day - 1} + \mu_1 \\
\text{elif}\ &dayIdx > cp-1: \\
&\quad \mu = text_{day - 1} + \mu_2 \\
text_{day} &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma) \\
\end{align*}
$$
1.モデルの定義
dataの日付day の値を -1 して日付インデックスを作成します。
### 日付インデックスday-1の作成
day_idx = data['day'].values - 1なお、テキストでは累積執筆量を1000分の1にしてStan処理をしていますが、この記事では1000分の1しないようにしています。
続いてモデルの定義に移ります。
今回は、7つの原稿を「ほぼ同一のモデルを原稿ごとに別々に構築する」ので、モデル定義~MCMC実行~事後予測サンプリング実行までを関数化して、原稿ごとに関数を呼び出す処理の流れにします。
### MCMC実行関数1 正規分布モデル
def exec_mcmc1(draft_col, disp=False):
with pm.Model() as model1:
### データ関連定義
# coordの定義
model1.add_coord('data', values=data.index, mutable=True)
# dataの定義
text = pm.ConstantData('text', value=data[draft_col].values,
dims='data')
dayIdx = pm.ConstantData('dayIdx', value=day_idx, dims='data')
### 事前分布
mu1 = pm.Uniform('mu1', lower=-100000, upper=100000)
mu2 = pm.Uniform('mu2', lower=-100000, upper=100000)
sigma = pm.Uniform('sigma', lower=0, upper=100000)
cp = pm.DiscreteUniform('cp', lower=1, upper=data['day'].max())
### muの計算
mu = pt.switch(pt.eq(dayIdx, 0), mu1,
pt.switch(pt.le(dayIdx, cp-1),
text[dayIdx-1] + mu1, text[dayIdx-1] + mu2))
### 尤度
likelihood = pm.Normal('likelihood', mu=mu, sigma=sigma, observed=text,
dims='data')
### モデルの表示・可視化 disp引数=Trueの場合に実行
if disp:
display(model1)
display(pm.model_to_graphviz(model1))
### 事後分布からのサンプリング
idata1 = pm.sample(draws=5000, tune=25000, chains=4, target_accept=0.95,
random_seed=1234)
### 事後予測サンプリング
idata1.extend(pm.sample_posterior_predictive(idata1))
return idata1【関数の処理の構成】
① PyMCモデルの定義:データ関連定義~尤度
② モデルの表示:モデルの表示・可視化
③ 事後分布からのサンプリング
④ 事後予測サンプリング
【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の1つを設定しました。
・行の座標:名前「data」、値「行インデックス」dataの定義
目的変数$${text}$$、日付インデックス$${dayIdx}$$を設定しました。パラメータの事前分布
$${\mu_1}$$、$${\mu_2}$$は$${[-100000, 100000]}$$の範囲をとる連続一様分布にしています。テキストでは$${[-100, 100]}$$としていますが、この記事では累積執筆量を1000分の1していないため、連続一様分布の範囲を1000倍しました。
同様に、$${\sigma}$$は$${[0, 100000]}$$の範囲をとる連続一様分布です。
変化点$${cp}$$は経過日数$${[1, 123]}$$を範囲にとる離散一様分布です。
muの計算
経過日数が変化点以下のとき、前日の累積執筆量に$${\mu_1}$$を加算し、変化点を超えるとき、前日の累積執筆量に$${\mu_2}$$を加算します。尤度
$${\mu}$$と$${\sigma}$$をパラメータにする正規分布に従います。
【事後分布のサンプリング】
離散型分布に従うパラメータがありますので、NUTSサンプラーはPyMC標準のサンプラーを用います。
numpyro利用時にくらべて、処理時間が増加します。
かつ、tune(バーンイン期間)を25000(テキストは500)に増量しているので、処理時間がかかる要因になっています。
2.MCMC関数の実行
for文で7つの原稿を一気に推論します。
処理時間はおよそ36分です。
### 事後分布&事後予測サンプリングの実施 尤度:正規分布 36分
# 原稿1~7までの推論データを格納するリストの初期化
idata1 = []
# 原稿1~7まで繰り返し処理
for i, col in enumerate(data.columns[1:]):
# 原稿の番号を表示
print(f'--- {i+1} ---')
disp = False
# 原稿1のとき、PyMCモデルを可視化
if i==0:
disp = True
# 事後分布&事後予測のサンプリングを実施、リストに推論データを格納
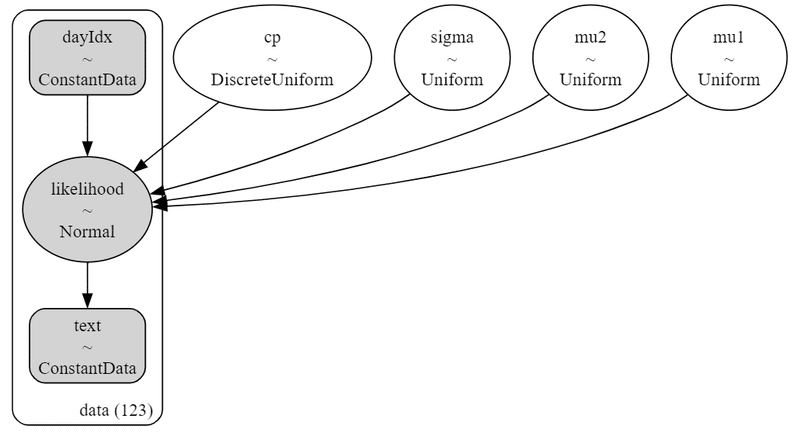
idata1.append(exec_mcmc1(col, disp=disp))【実行結果1:モデルの表示・可視化】
シンプルめのモデルです。
同一の型のモデルを7つの原稿に対して適用します。
原稿ごとにモデルを定義し直しているので、推論値は原稿ごとに算定されます。

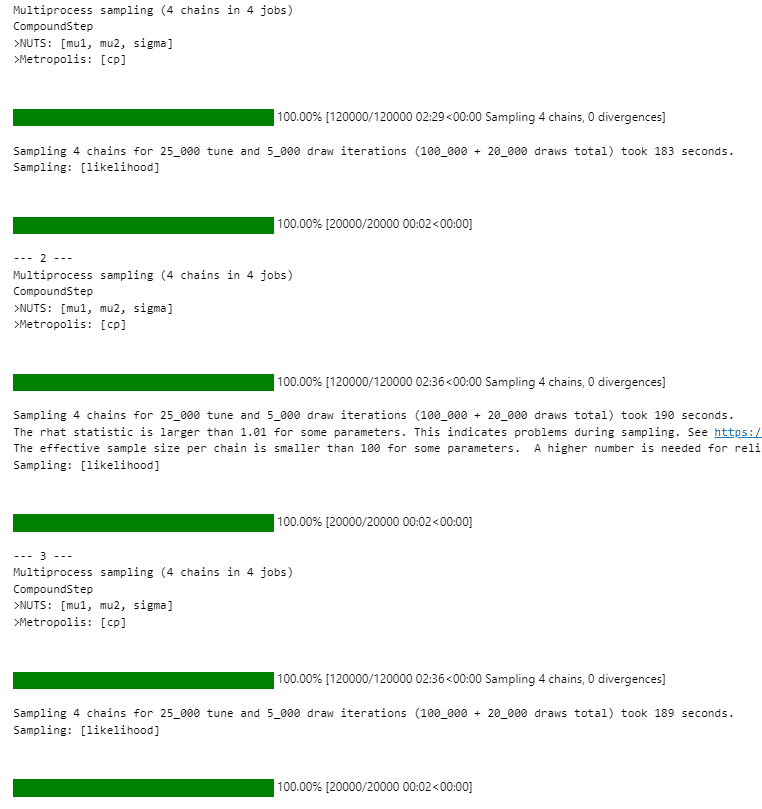
【実行結果2:MCMC・事後予測】
こちらは原稿1~3です。
こちらは原稿4~6です。
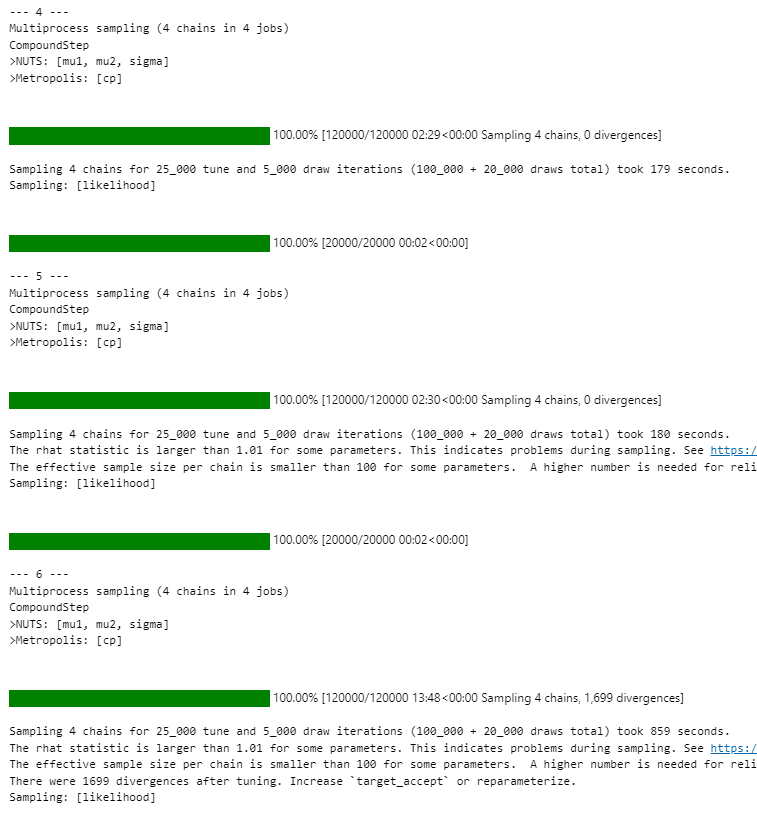
こちらは原稿7です。
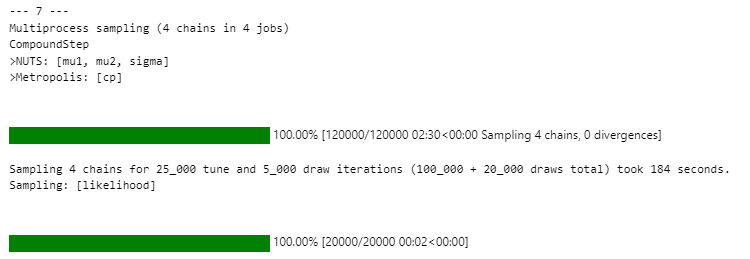
原稿6は、処理時間が長くて発散したデータ数が多いようです。
テキストやRコードで原稿6に対する言及(cpの範囲が広い、推定に時間がかかる)されており、原稿6には何かがついているのかもしれません。
3.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R}\leq 1.1}$$としています。
### r_hat>1.1の確認
# 原稿1~7まで繰り返し処理
for i in range(len(idata1)):
# 原稿の番号を表示
print(f'--- {i+1} ---')
# R_hatの算出
rhat_idata = az.rhat(idata1[i].posterior)
# R_hat > 1.1となる変数の数を表示
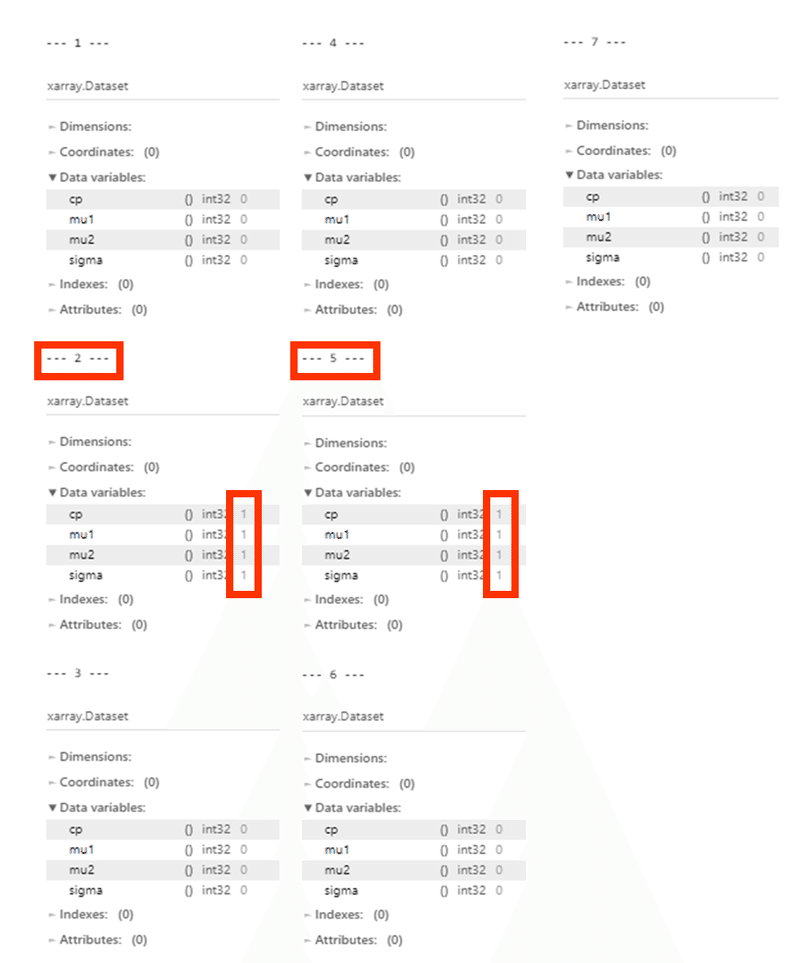
display((rhat_idata > 1.1).sum())【実行結果】
原稿2,5のパラメータが$${\hat{R} > 1.1}$$となり、収束していません。
原稿2,5のような「徐々に原稿を書く」場合には、モデルの改良が必要なのかもしれません。
以後、データを用いる際に、原稿2,5は正式な分析ができず、参考値の扱いになる点に注意して下さい。
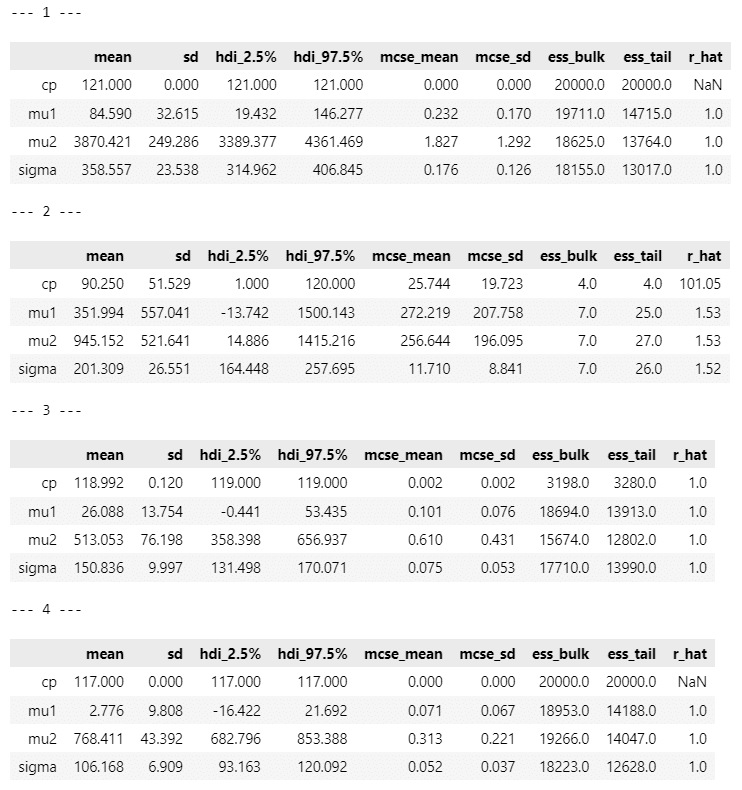
推論データの要約統計量です。
### 推論データの要約統計量の表示
# 原稿1~7まで繰り返し処理
for i in range(len(idata1)):
# 原稿の番号を表示
print(f'--- {i+1} ---')
# 推論データの要約統計量の表示
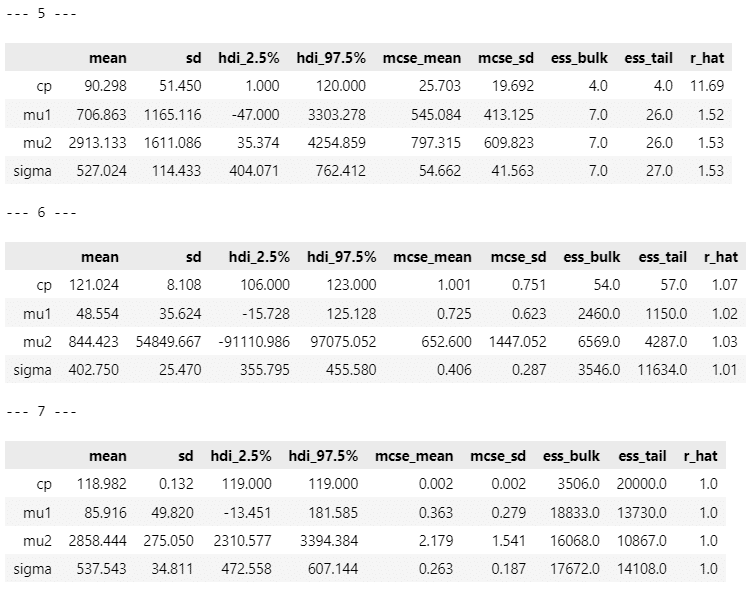
display(pm.summary(idata1[i], hdi_prob=0.95))【実行結果】
$${cp}$$の平均値 mean に注目します。
小数点第一位を四捨五入して整数値にすると、テキストの表14.2に掲載の「変化点」と一致するのは、原稿1,3,4,7です。
原稿6は全6016文字中、93日に一気に3800文字を書いたことが推論値のブレに繋がったのかもしれません。$${\mu_2}$$の 95%HDI が$${[-91111, 97075]}$$というありえない値になっています。
原稿6はこのモデルと相性がよくないのかもです。
トレースプロットです。
### トレースプロットの描画
# 原稿1~7まで繰り返し処理
for i in range(len(idata1)):
# 原稿の番号を表示
print(f'--- {i+1} ---')
# トレースプロットの描画
pm.plot_trace(idata1[i], figsize=(10, 6))
plt.tight_layout()
plt.show()【実行結果】
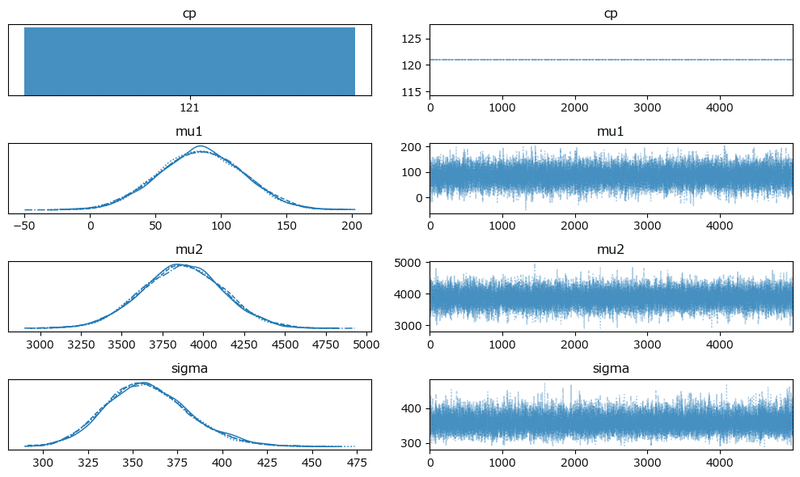
原稿1:
変化点は121日じゃ!という強い主張が聞こえてきそうです。
きれいな描画になりました。
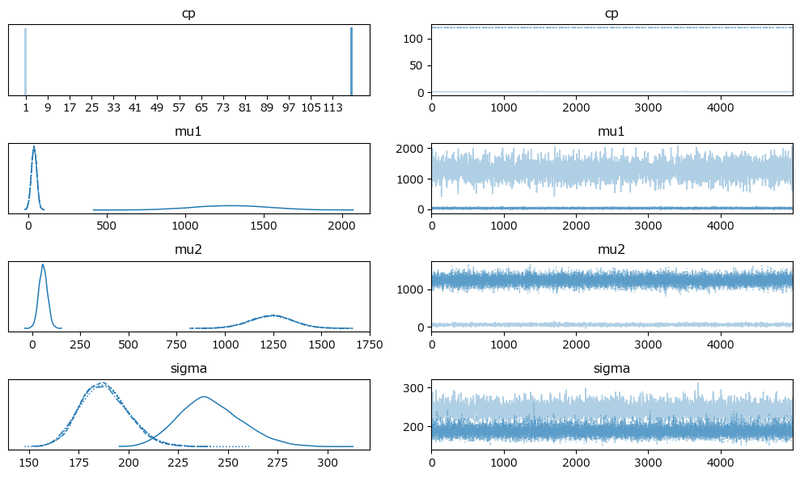
原稿2:
4つのchainが2つの分布に分かれています。
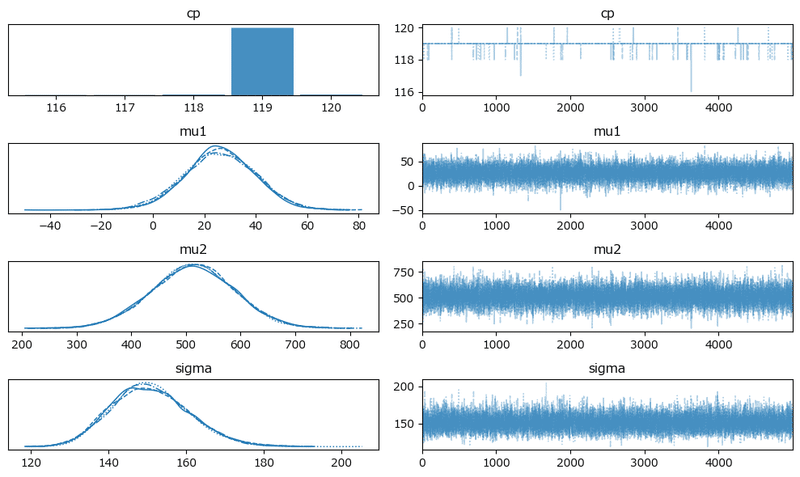
原稿3:
変化点はほぼほぼ119日ですね!
原稿4:
変化点は117日!
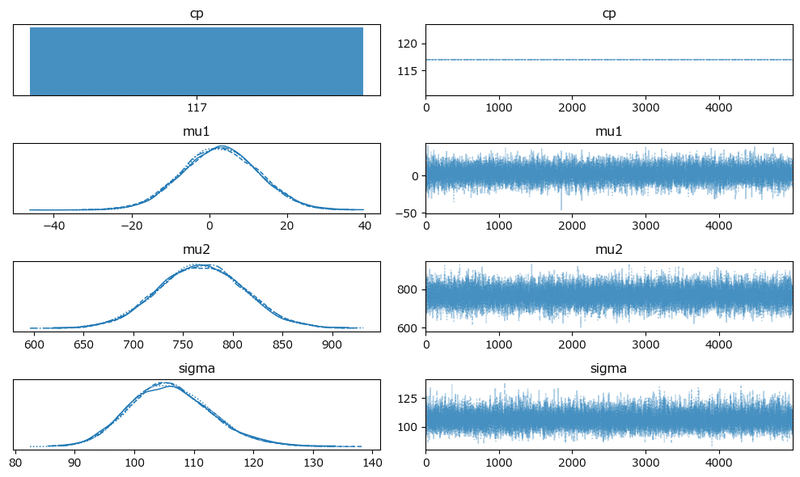
原稿5:
分布が2つに別れています。
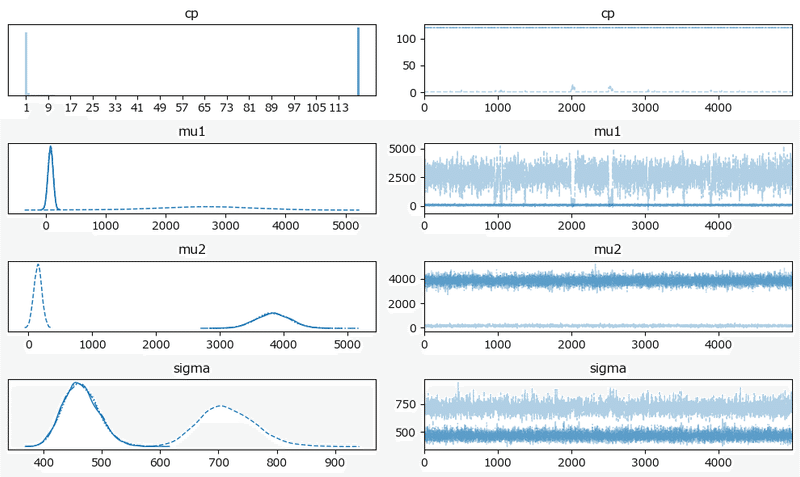
原稿6:
発散を示すバーコードが散見されます。
分布の中心は4つのchainで一致しているような感じです。
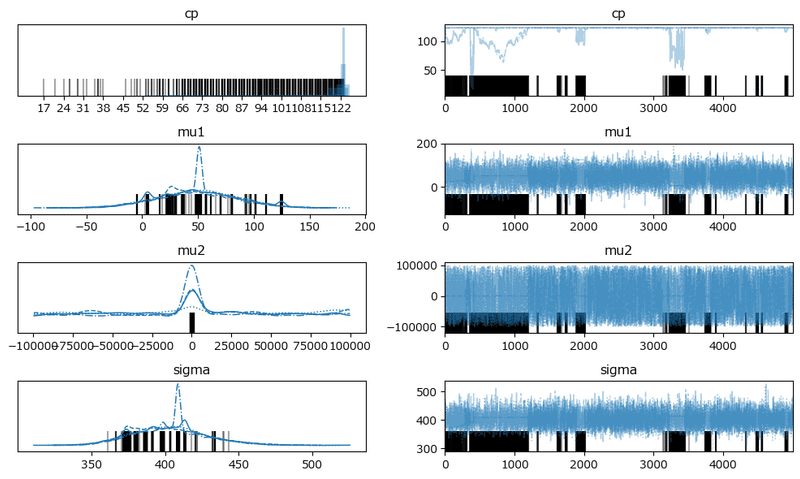
原稿7:
変化点はほぼほぼ119日です!
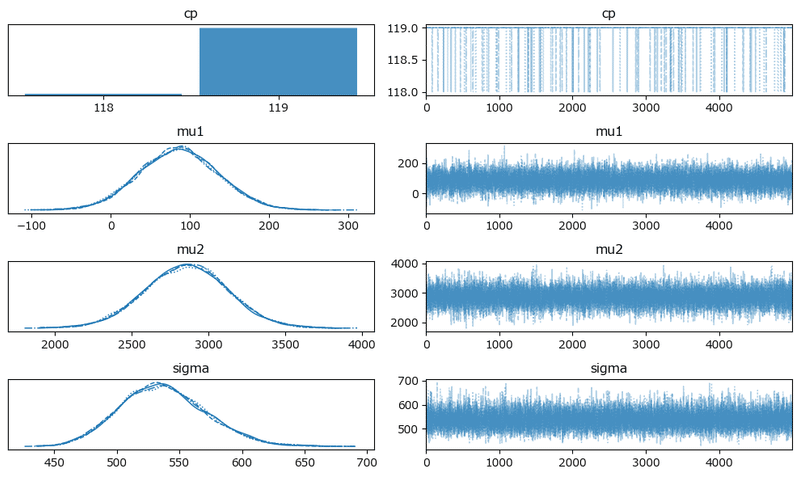
5.分析
テキストの図14.4に相当する変化点を追加した各原稿の執筆状況を描画します。
目的変数(text)の事後予測値を用いています。
### 変化点を追加した各原稿の執筆状況 ★図14.4に対応
plt.figure(figsize=(10, 10))
for i in range(len(idata1)):
## 変化点の平均の算出
cp_mean = idata1[i].posterior.cp.mean().values
# 95%HDI区間の算出
hdi95 = (az.hdi(idata1[i].posterior_predictive, hdi_prob=0.95)
.likelihood.data)
## 描画
ax = plt.subplot(4, 2, i+1)
# 95%HDIの描画
ax.fill_between(x=data['day'], y1=hdi95[:, 0], y2=hdi95[:, 1],
color='tomato', alpha=0.4)
# 事後予測の平均値の描画
ax.plot(data['day'],
(idata1[i].posterior_predictive.likelihood.data.reshape(20000, 123)
.mean(axis=0)))
# 観測値の描画
ax.plot(data['day'], data.iloc[:, i+1], 'o', markersize=1, color='blue')
# 変化点の描画
ax.axvline(cp_mean, color='black', lw=0.8, ls='--')
# 修飾
ax.set_title(f'原稿 {i+1}: 変化点{cp_mean:.0f}日')
plt.tight_layout()
plt.show()【実行結果】
青点が観測値、青い折れ線が事後予測値の平均値、赤い帯が事後予測値の95%HDI、黒い垂直点線が変化点です。
事後予測はうまくいっている感じがします。
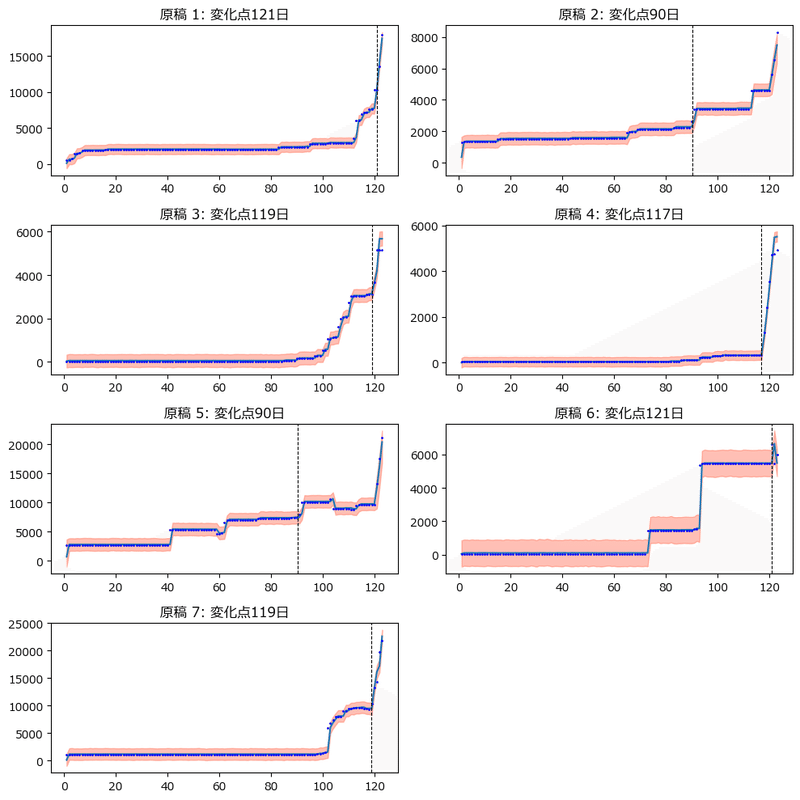
【分析】
■ 論点1:変化点1つのモデルの適否
①原稿1,3,4,7の変化点
急激に執筆量が増加する時点が1つだけ存在するので、変化点が1つのモデルで表現しやすい(適合させやすい)ように感じます。
②原稿6
変化点が70日付近、90日付近、120日付近の3段階あるので、変化点が1つのモデルでは表現しきれないように感じます。
③原稿2,5
こちらも多段階の変化点を観察できます。
モデルが合わないことが収束しない主因なのかもしれません。
(なぜテキストは収束できたのでしょう???)
■ 論点2:執筆量の変化が生じるタイミングに対する論考
調査・実験の実施、データの取りまとめと分析、論文化の流れの中で、論文執筆が後半になるのは通常運転のような気がします。
一方で、ほぼほぼ執筆材料が揃っていて論文化・清書だけすればよい状態の場合、123日間のうちの最後の数日で書き上げるようなスタイルは計画性の無さを露呈しかねない状況と言えるでしょう。
おそらく著者は前者ではないかと推察いたします。
だってコード作成までして計画的に執筆量管理の仕組みを構築できた方なのですから。
6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idata1の保存 pickle
file = r'idata1_ch14.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch14.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)以上で第13章は終了です。
表14.3、図14.5、図14.6は省略しました。
おまけ
書籍「Pythonで体験するベイズ推論」でお馴染みの変化点検出モデルを試してみます。
この書籍はPyMCによるベイズ推論に関する豊富な例題が掲載されていて、ベイズを身近にできるおすすめの一冊です。
結論から述べます。
・原稿1が収束しませんでした。
・最初の変化点を拾いやすいモデルになりました。
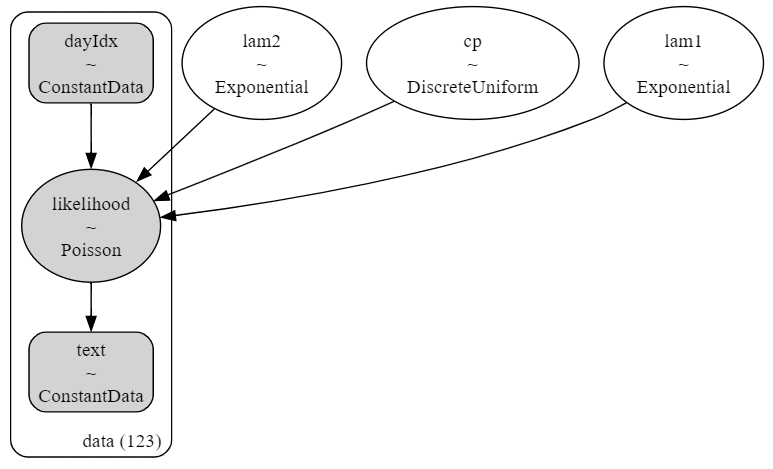
モデルは、観測値がポアソン分布に従います。
ポアソン分布の平均パラメータ$${\lambda}$$は変化点$${cp}$$前後で別個になります。
平均パラメータ$${\boldsymbol{\lambda}}$$は指数分布に従います。
モデルのイメージを共有いたします。

1.MCMC実行関数の定義
### MCMC実行関数2 ポアソン分布モデル
def exec_mcmc2(draft_col, disp=False):
with pm.Model() as model2:
# 初日の執筆量の最小値の逆数
alpha1 = 1 / data.iloc[0, 1:].min()
# 1原稿の最大執筆量の逆数
alpha2 = 1 / data.iloc[:, 1:].max().max()
### データ関連定義
# coordの定義
model2.add_coord('data', values=data.index, mutable=True)
# dataの定義
text = pm.ConstantData('text', value=data[draft_col].values,
dims='data')
dayIdx = pm.ConstantData('dayIdx', value=day_idx, dims='data')
### 事前分布
lam1 = pm.Exponential('lam1', lam=alpha1)
lam2 = pm.Exponential('lam2', lam=alpha2)
cp = pm.DiscreteUniform('cp', lower=1, upper=data['day'].max())
### muの計算
mu = pt.switch(pt.eq(dayIdx, 0), lam1,
pt.switch(pt.le(dayIdx, cp-1),
text[dayIdx-1] + lam1, text[dayIdx-1] + lam2))
### 尤度
likelihood = pm.Poisson('likelihood', mu=mu, observed=text, dims='data')
### モデルの表示・可視化 disp引数=Trueの場合に実行
if disp:
display(model2)
display(pm.model_to_graphviz(model2))
### 事後分布からのサンプリング
idata2 = pm.sample(draws=5000, tune=25000, chains=4, target_accept=0.95,
random_seed=1234)
### 事後予測サンプリング
idata2.extend(pm.sample_posterior_predictive(idata2))
return idata22.MCMC等の実行
処理時間はおよそ24分35秒です。
### 事後分布&事後予測サンプリングの実施 尤度:ポアソン分布 24分35秒
# 原稿1~7までの推論データを格納するリストの初期化
idata2 = []
# 原稿1~7まで繰り返し処理
for i, col in enumerate(data.columns[1:]):
# 原稿の番号を表示
print(f'--- {i+1} ---')
disp = False
# 原稿1のとき、PyMCモデルを可視化
if i==0:
disp = True
# 事後分布&事後予測のサンプリングを実施、リストに推論データを格納
idata2.append(exec_mcmc2(col, disp=disp))【実行結果】省略
3.サンプリングデータの確認
まずは収束の確認です。
### r_hat>1.1の確認
# 原稿1~7まで繰り返し処理
for i in range(len(idata2)):
# 原稿の番号を表示
print(f'--- {i+1} ---')
# R_hatの算出
rhat_idata = az.rhat(idata2[i].posterior)
# R_hat > 1.1となる変数の数を表示
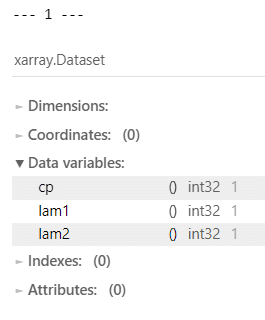
display((rhat_idata > 1.1).sum())【実行結果】原稿1のみ掲載
原稿1が収束しませんでした。
続いて要約統計量の表示。
### 推論データの要約統計量の表示
# 原稿1~7まで繰り返し処理
for i in range(len(idata2)):
# 原稿の番号を表示
print(f'--- {i+1} ---')
# 推論データの要約統計量の表示
display(pm.summary(idata2[i], hdi_prob=0.95))【実行結果】
変化点$${cp}$$前の平均パラメータ lam1 の方が$${cp}$$後の lam2 よりも値が大きい原稿があるのが不可解です。
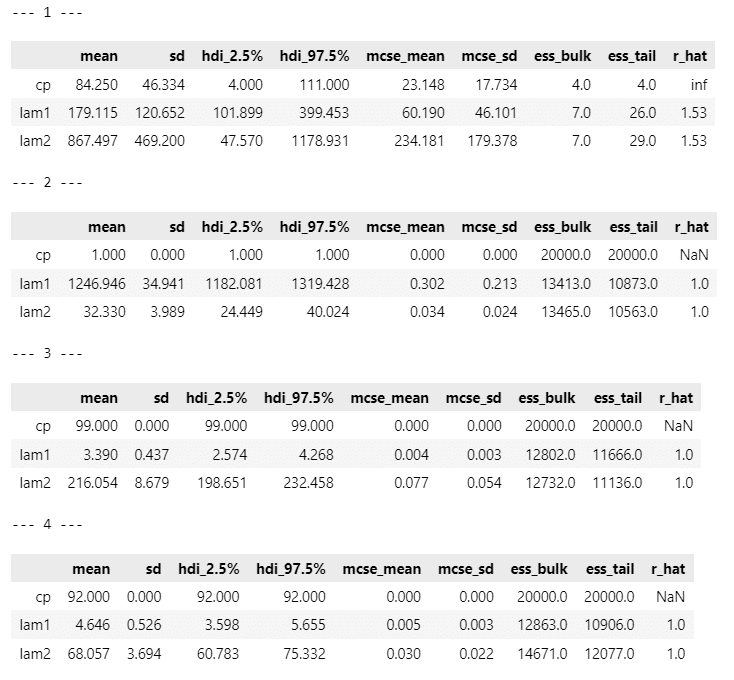
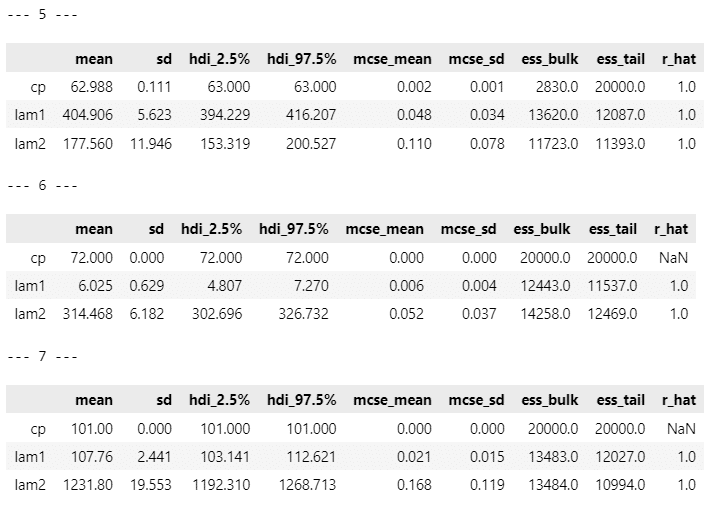
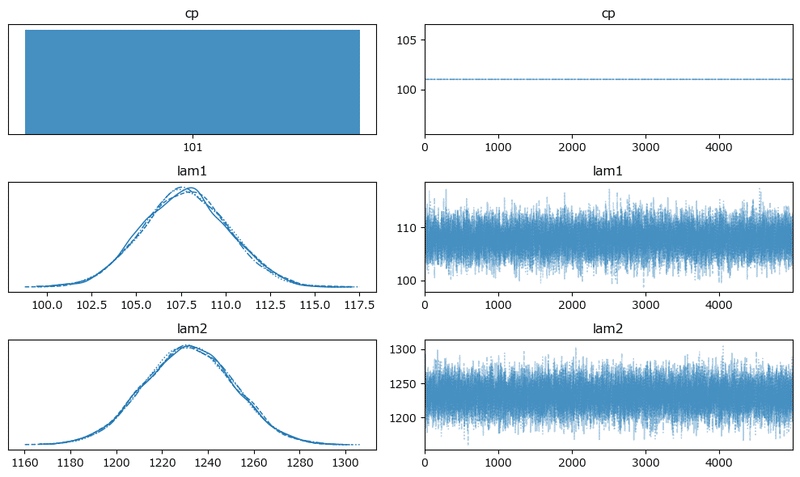
トレースプロットの確認です。
### トレースプロットの描画
# 原稿1~7まで繰り返し処理
for i in range(len(idata2)):
# 原稿の番号の表示
print(f'--- {i+1} ---')
# トレースプロットの描画
pm.plot_trace(idata2[i], figsize=(10, 6))
plt.tight_layout()
plt.show()【実行結果】
原稿1:
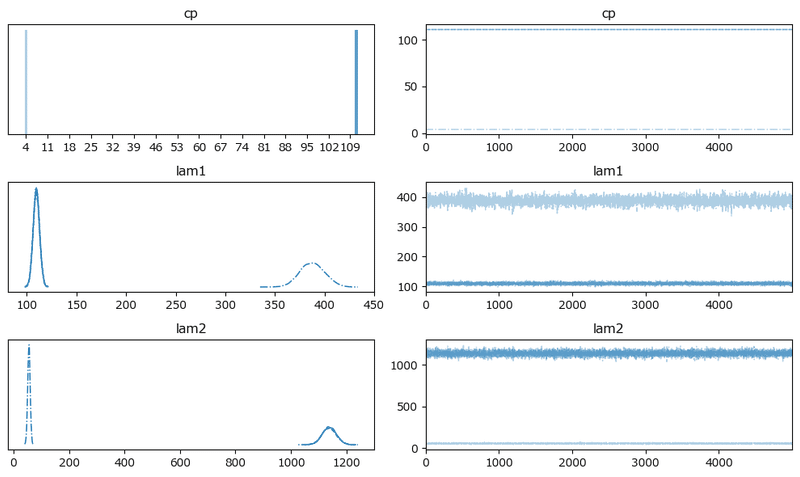
原稿2:
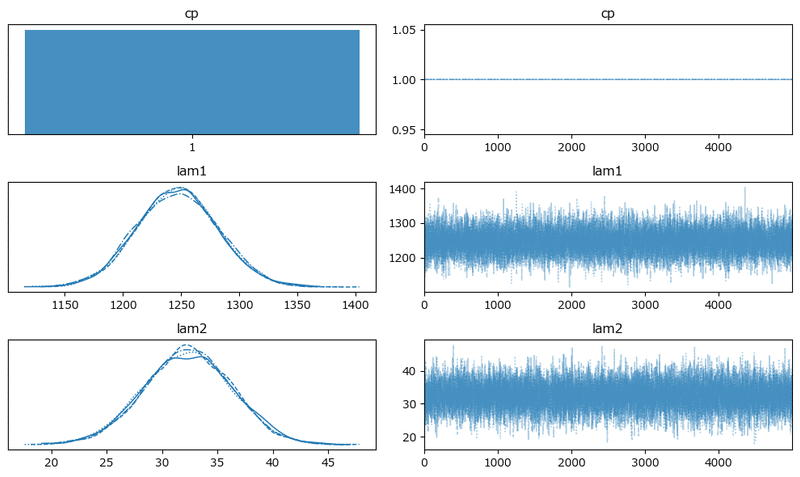
原稿3:
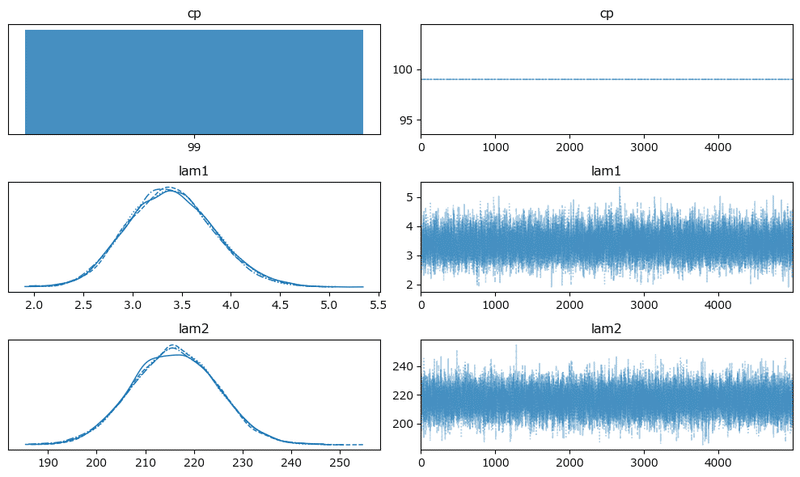
原稿4:
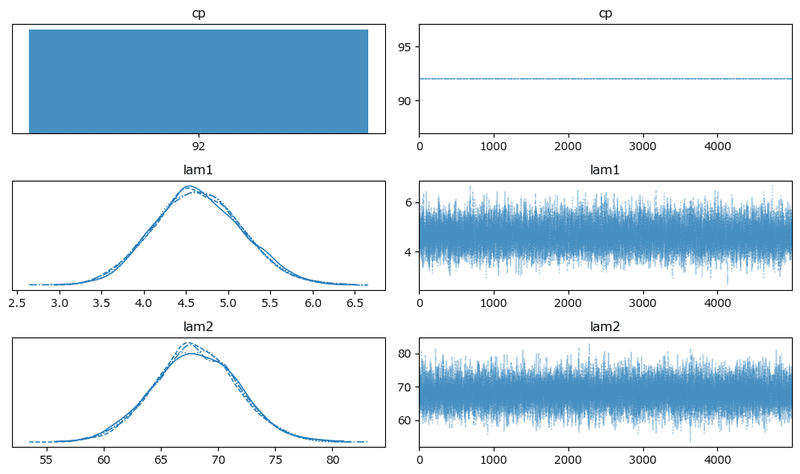
原稿5:
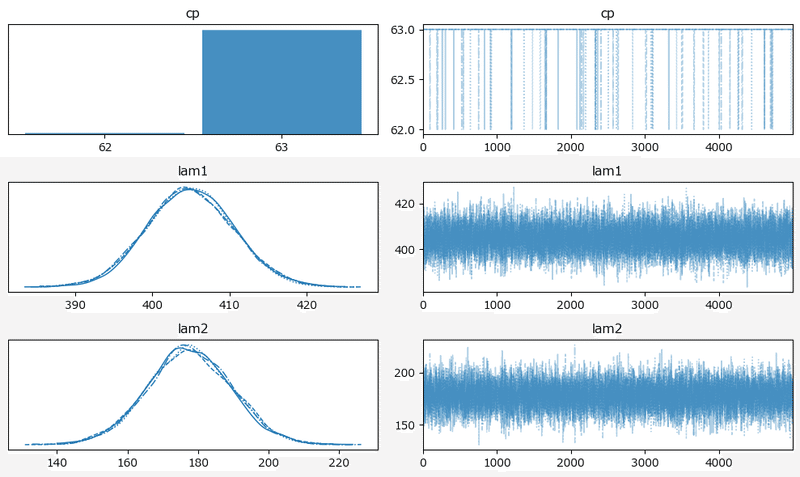
原稿6:
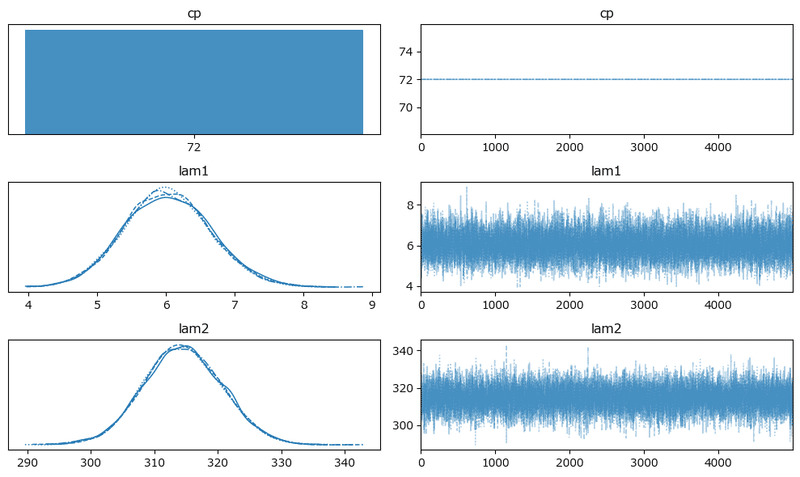
原稿7:
4.分析
さあ、いよいよ、変化点を追加した原稿の執筆状況の描画です。
### 変化点を追加した各原稿の執筆状況 ★図14.4に対応
plt.figure(figsize=(10, 10))
for i in range(len(idata2)):
## 変化点の平均の算出
cp_mean = idata2[i].posterior.cp.mean().values
# 95%HDI区間の算出
hdi95 = (az.hdi(idata2[i].posterior_predictive, hdi_prob=0.95)
.likelihood.data)
## 描画
ax = plt.subplot(4, 2, i+1)
# 95%HDIの描画
ax.fill_between(x=data['day'], y1=hdi95[:, 0], y2=hdi95[:, 1],
color='tomato', alpha=0.9, label='事後分布95%HDI')
# 事後予測の平均値の描画
ax.plot(data['day'],
(idata2[i].posterior_predictive.likelihood.data.reshape(20000, 123)
.mean(axis=0)))
# 観測値の描画
ax.plot(data['day'], data.iloc[:, i+1], 'o', markersize=1, color='blue')
# 変化点の描画
ax.axvline(cp_mean, color='black', lw=0.8, ls='--')
# 修飾
ax.set_title(f'原稿 {i+1}: 変化点{cp_mean:.0f}日')
plt.tight_layout()
plt.show()【実行結果・分析っぽい推論】
このモデルはまるで「執筆量のささやかな変化の兆候」を機敏にすくい取るかのようです。
やる気スイッチがONになる絶好のタイミング=予兆を検知するプレミアムモデルに昇華できるかもしれません!!!!
原稿2は初日からターボ全開!(になるパラレルワールドがあったかも)
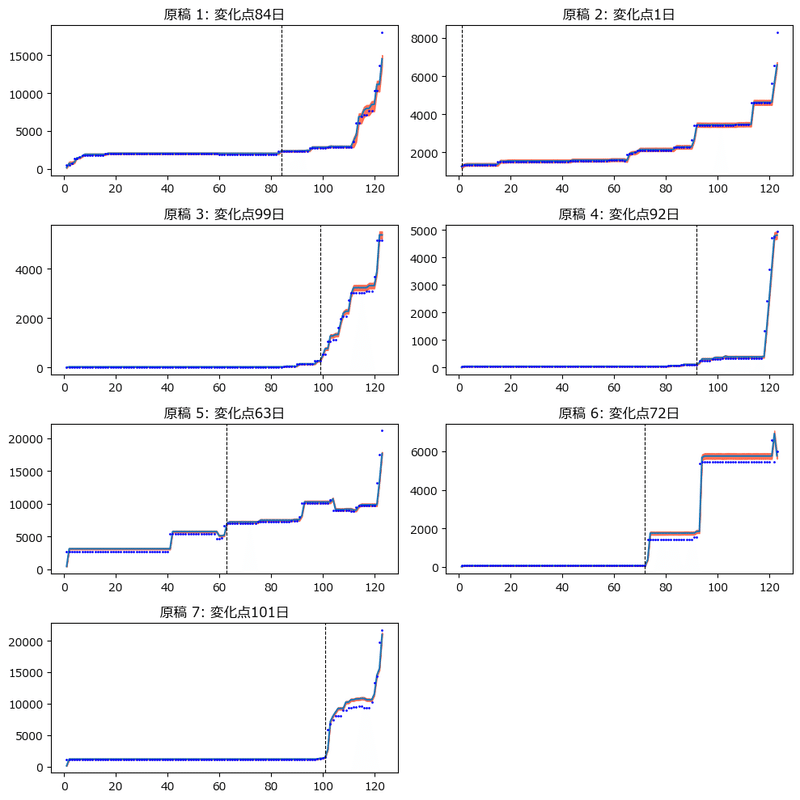
それにしても、95%HDIを示す赤い帯の幅が超狭い=ほぼ平均値になるという推論、って凄いですね。
おまけモデルは以上です。
おわりに
ブログ原稿の執筆
第14章のモデルに取り組むにあたって、自分のブログ原稿の執筆態度を振り返ってみました。
締め切り
仕事や公的な作業では無いため、締め切りは無いも同然w
一応、週1ペースで投稿するつもりでいるので、自らを律することで締め切りという概念を顕在化させられます。計画
計画はありません!スケジュール、WBSなどを作成していませんし、実績を把握したり進捗を管理することなどしていません。
自由気ままに書けるのが私的ブログの醍醐味ですヽ(=´▽`=)ノ管理
管理していません(断言!キリッ!)。
楽しい趣味だから毎日楽しく描き続けられるのです!
一応、目安はあります。ストックを4~5つ貯めておくことです。楽しさの源泉
テキストを楽しく学んだ結果をブログに書くだけのこと。
そしてブログ執筆が楽しいというよりも、学ぶことが楽しいです(趣味:学び)。
またWeb検索で欲しい技術情報・ヒントが日本語で得られる環境に憧れています。
私のレアな(時に失敗作が)ブログが、ニッチを探す誰かのお役に立てたなら幸いです🍀
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
