今回の統計トピック

復元抽出による標本平均$${\bar{X}}$$（Xバー）の中央値と最頻値を調べます。
そして標本平均が正規分布に近似する「中心極限定理の実験」を実施します！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

標本分布の分野
問2 標本分布の中央値等（データなし）

試験実施年月
統計検定2級 2019年6月 問13（回答番号23）

問題

公式問題集をご参照ください。

解き方

題意
既知の母集団｛２，４，６，８｝から無作為復元抽出で標本サイズ２の標本$${X_1,\ X_2}$$を抽出するとき、標本平均$${\bar{X}}$$の中央値と最頻値を求めます。

実直に標本$${X_1,\ X_2}$$の組み合わせ表を作成して調べます。

組み合わせ表で最頻値を調べる
組み合わせは$${4\times4=16}$$通りであり、それぞれの組み合わせの確率は均等に$${1/4 \times 1/4 = 1/16}$$になります。

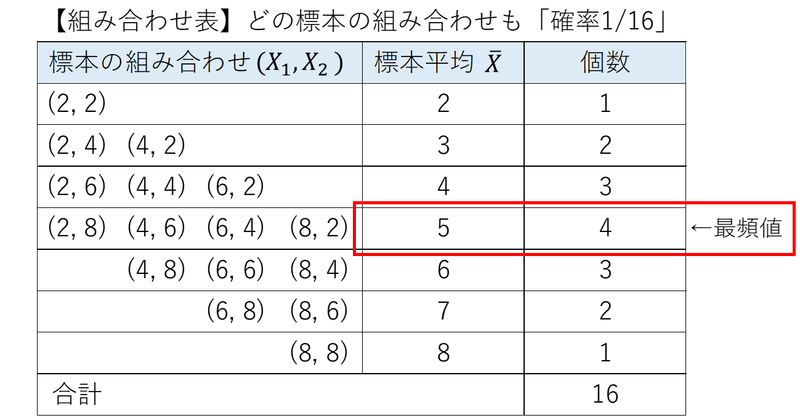
この表から、標本平均$${\bar{X}}$$の最頻値が$${5}$$であることが分かりました。

標本平均を昇順で並べて中央値を調べる
中央値を調べるため、標本平均全１６個を昇順で並べます。
組み合わせ表の標本平均$${\bar{X}}$$の値を「個数」の分だけ並べます。

この図から、標本平均$${\bar{X}}$$の中央値が$${5}$$であることが分かりました。

単一の標本の分布と標本平均の分布の違いを確認しましょう。

標本平均$${\boldsymbol{\bar{X}}}$$と正規分布近似 
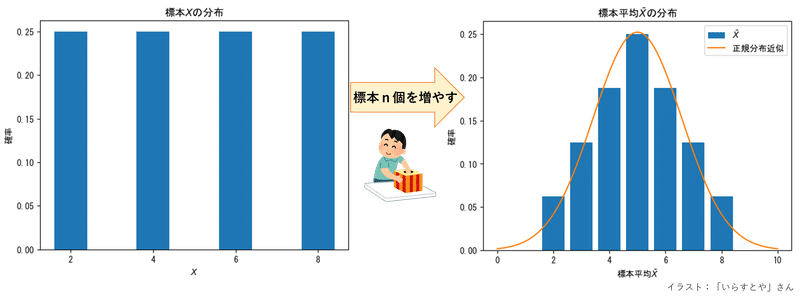
母集団から｛２，４，６，８｝を１つ無作為抽出するとき、各値の出る確率はすべて１／４です。
標本$${X_i}$$の分布は一様分布です。

ところが、標本平均$${\bar{X}}$$の分布は大きく変わります。
ベル型の正規分布の形状に近づいているのです！
次のヒストグラムは、組み合わせ表の標本平均$${\bar{X}}$$と個数を用いて描画しました。

標本平均$${\bar{X}}$$の重要な性質「標本サイズ$${n}$$が大きくなると正規分布に近似する」なのです！
「知る」で深掘りしましょう！

解答

③ (5.0, 5.0) です。

難易度　やさしい

・知識：標本平均、中央値、最頻値
・計算力：組み合わせ表（低い）
・時間目安：1分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、中心極限定理をひも解いて標本平均と正規分布の関係の謎に迫ります！
実験をします！

標本分布

📕公式テキスト：2.10 標本分布（86ページ～）
母集団から標本を無作為抽出するとき、標本の統計量が従う確率分布を標本分布と呼びます。
標本平均が従う分布は標本分布です。

標本平均
標本の大きさ$${n}$$個の標本平均の公式です。

中心極限定理

📕公式テキスト：2.11.3 中心極限定理（93ページ～）

母集団が正規分布に従っていなくても、標本サイズ$${n}$$が大きいならば、標本平均$${\bar{X}}$$の分布が正規分布$${N (\mu, \frac{\sigma}{\sqrt{n}} )}$$に近似するのです。

ということで、中心極限定理をPythonで実験してみましょう！
標本平均$${\bar{X}}$$が「平均＝母平均$${\mu}$$」、「分散＝$${\sigma/\sqrt{n}}$$＝$${母分散/\sqrt{標本サイズ}}$$」の正規分布に近づくかどうかを確認するのです！

中心極限定理の実験

０から１００までの整数１千万個をもつ母集団から、$${n}$$個の標本を無作為復元抽出して標本平均$${\bar{X}}$$を求める試行を、１万回行います。

母集団のプロフィール
母集団のデータは一様分布の乱数で取得します。
母集団データをヒストグラムで可視化しましょう。
一様分布に従っている様子がよく分かります。

標本サイズ$${n}$$をどんどん大きくして、中心極限定理を確認します。

標本サイズ 10 のケース
まずは、標本サイズ10から。
すでに正規分布に近い感じがします。

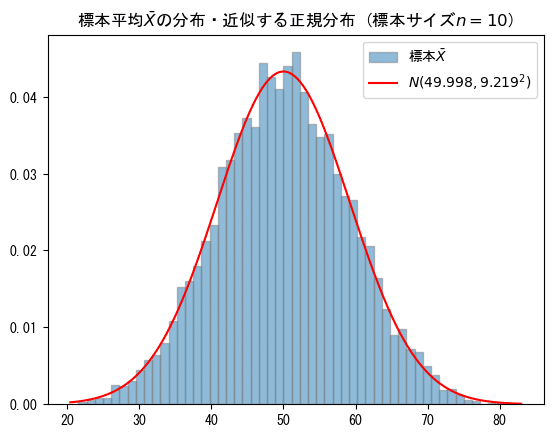
【平均、標準偏差】標準偏差がまだまだ乖離しています。
■母集団データ
・母平均μ=49.9984575, 母標準偏差σ=29.153640934207406
■標本平均の分布が正規分布に近似するとき
・標本平均X_bar=49.9984575, 標本標準偏差σ/√n=9.219190743881448
■実際の標本データ
・標本平均X_barの平均=50.019960000000005,
　不偏分散の標準偏差s=83.97396099449945

標本サイズ 100 のケース
続いて標本サイズ100です。
標本平均$${\bar{X}}$$の実現値のとる範囲が$${50 \pm 10}$$くらいに、どんどん狭くなっています。

【平均、標準偏差】標準偏差が近づいてきました。
■母集団データ
・母平均μ=49.9984575, 母標準偏差σ=29.153640934207406
■標本平均の分布が正規分布に近似するとき
・標本平均X_bar=49.9984575, 標本標準偏差σ/√n=2.9153640934207408
■実際の標本データ
・標本平均X_barの平均=50.023233999999995,
　不偏分散の標準偏差s=8.483845965840583

標本サイズ 1000 のケース
続いて標本サイズ1000です。
標本平均$${\bar{X}}$$の実現値のとる範囲が$${50 \pm 3}$$くらいに、どんどん狭くなっています。

【平均、標準偏差】平均・標準偏差ともに近似しています。
■母集団データ
・母平均μ=49.9984575, 母標準偏差σ=29.153640934207406
■標本平均の分布が正規分布に近似するとき
・標本平均X_bar=49.9984575, 標本標準偏差σ/√n=0.9219190743881448
■実際の標本データ
・標本平均X_barの平均=49.988660499999995,
　不偏分散の標準偏差s=0.8387236688066306

標本サイズ 10000 のケース
続いて標本サイズ10000です。
標本平均$${\bar{X}}$$の実現値のとる範囲が$${50 \pm 1}$$くらいに、どんどん狭くなっています。

【平均、標準偏差】実際のデータの標準偏差が極めて小さくなりました。
■母集団データ
・母平均μ=49.9984575, 母標準偏差σ=29.153640934207406
■標本平均の分布が正規分布に近似するとき
・標本平均X_bar=49.9984575, 標本標準偏差σ/√n=0.29153640934207403
■実際の標本データ
・標本平均X_barの平均=50.00577449000001,
　不偏分散の標準偏差s=0.08464575892013193

横軸の表示範囲をサイズ 10 と同じ 20 ～ 80 に広げてみましょう。
実はこんなに尖っています。母集団の平均に集まっています。

標本平均$${\bar{X}}$$は標本サイズ$${n}$$が多くくなるにつれて、分散が小さくなり、尖った正規分布へと近づいていく様子が分かりました。

長旅、お疲れ様でした。

実践する

中心極限定理の実験をしてみよう

「知る」の中心極限定理の実験をしましょう。
EXCELとPythonを活用します。

電卓・手作業で作成してみよう！

「知る」「EXCELで作成してみよう！」の内容などをご覧いただき、「標本平均の分布」のイメージに近づいてください！

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

一様分布の乱数の生成
RANDBETWEEN関数を用いて、0から100までの整数の乱数を生成します。「=RANDBETWEEN(0,100)」です。

実験では 200個 の乱数を 100回 試行して生成しました。
乱数表の一部を紹介いたします。

なお、乱数（RANDBETWEEN関数）をそのまま放置すると、EXCELの計算の都度、乱数が変わってしまいます。
そこで、データの値をコピーして、乱数が変化しないようにしました。
したがって、乱数表には「RANDBETWEEN関数」がいなくなりました。

中心極限定理の実験
乱数を標本に見立てて、３つの標本サイズｎのケースを検討します。
・n=2：乱数２個の標本平均
・n=20：乱数２０個の標本平均
・n=200：乱数２００個の標本平均

標本平均表
標本平均表を作成します。
試行No.（最大100回）ごとに、n=2、n=20、n=200の標本平均をまとめます。
次は標本平均表（抜粋）のイメージです。

３つの標本平均データの統計量をまとめました。
標本サイズが大きくなるにつれて、不偏分散・標準偏差の値が小さくなっています。

相対度数分布表
標本平均表から相対度数分布表を作成します。

標本平均の分布
相対度数分布表からグラフを作成します。

標本サイズ n=2 のときは平らな形状をしています。
標本サイズが n=20、n=200 へと大きくなるにつれて、平均を中心にして立ち上がり、ベル型の正規分布の形状に近づいていますね！

中心極限定理「標本サイズが大きくなると正規分布に近づく」を体感できたでしょうか。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、「知る」の章で用いた中心極限定理の実験のPythonコードです。

①インポート

import random
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②中心極限定理の実験

■一様分布の乱数で母集団のデータを取得
numpy の random.randint で 0 から 100 までの一様分布乱数を取得します。

# 設定 母集団のサイズ（母集団のデータ数）
pop_size = 10000000

# 母集団の0～100の整数データを生成
np.random.seed(1)
pop_data = np.random.randint(low=0, high=101, size=pop_size)

# 母平均mu、母標準偏差sigmaの算出
mu = np.mean(pop_data)
sigma = np.std(pop_data)

# 母集団のヒストグラムのプロット
bins = range(102)
plt.hist(pop_data, bins=bins)
plt.xlabel('データ値 $X$, $0 \leq X \leq 100$')
plt.ylabel('度数：データ数')
plt.title(f'一様分布の乱数 {pop_size}個')
plt.show()

■標本平均の確率分布の表示
標本サイズｎを設定します。
試行回数 num_trials の回数（コードでは10,000回）、標本採取を繰り返し実行します。
random.choices で母集団から標本サイズｎの無作為復元抽出を行い、np.meanで標本平均を算出しています。
乱数の関係で記事掲載内容と異なる結果になる場合があります。

# 設定 標本サイズ
n = 10000

# 初期化
num_trials = 10000    # 試行回数
x_mean_list = []
np.random.seed(1)

# 標本平均X_barが近似する標本平均・標本標準偏差の算出
X_bar_mu = mu
X_bar_sigma = sigma/np.sqrt(n)

# 母集団データからランダムに標本サイズnを復元抽出して
# 標本平均x_meanを算出、x_mean_listに格納する。
# 試行回数num_trialsの数の標本平均x_meanを採取する。
for i in range(num_trials):
    x_mean = np.mean(random.choices(pop_data, k=n))
    x_mean_list.append(x_mean)

# 標本平均x_meanの平均、標本不偏分散の標準偏差を算出・出力
x_mean_mean = np.mean(x_mean_list)
x_mean_S = np.var(x_mean_list, ddof=1)
print(f'母平均μ={mu}, 母標準偏差σ={sigma}')
print(f'標本平均X_bar={X_bar_mu}, 標本標準偏差σ/√n={X_bar_sigma}')
print(f'標本平均X_barの平均={x_mean_mean}, 不偏分散の標準偏差s={x_mean_S}')

# 標本平均が近似する正規分布の確率密度関数の値を取得
x_norm = np.linspace(min(x_mean_list), max(x_mean_list), 1001)
y_norm = norm.pdf(x_norm, X_bar_mu, X_bar_sigma)

# 試行で得た標本平均x_meanのヒストグラムをプロット
plt.hist(x_mean_list, bins='auto', density=True, ec='gray', alpha=0.5, label=f'標本$\\bar{{X}}$')
# 標本平均が近似する正規分布をプロット
plt.plot(x_norm, y_norm, c='red', label=f'$N({X_bar_mu:.3f},{X_bar_sigma:.3f}^2)$')

plt.title(f'標本平均$\\bar{{X}}$の分布・近似する正規分布 (標本サイズ$n={n}$)')
plt.legend()
plt.show()

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

実験～シミュレーションは楽しいですね！
PythonやEXCELなどの手軽に利用できるツールがあるので、実験に取り組みやすいです。
これからもさまざまな実験を行いたいです。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次