今回の統計トピック

引き続き分散分析を実践いたします。
10年以上にわたる「全国コンビニエンスストアの売上高」データを満喫しましょう！
なぜか時系列モデルを構築して未来の売上高を予測します！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」を１つの章にまとめます。
次に「実践する」で例題を用いて一元配置分散分析を手作業・EXCEL・R・Pythonで実践いたします。

問題を解きながら知る

📘公式問題集のカテゴリ

線形モデルの分野　～分散分析の分野
問2 平方和・自由度・結果の説明（コンビニの月別売上高）

試験実施年月
統計検定2級 2019年11月 問17（回答番号30,31,32）

📕公式テキスト：5.2.1 １元配置分散分析（185ページ～）

問題

公式問題集をご参照ください。

解き方

題意
問題文に記載された「2008年から2018年までの月別の売上高」データに基づいて、次の３問を解答します。
１．水準間平方和と残差平方和の数式
２．分散分析表の自由度の穴埋め
３．分散分析表に基づく統計的仮説検定の結論文章の適否

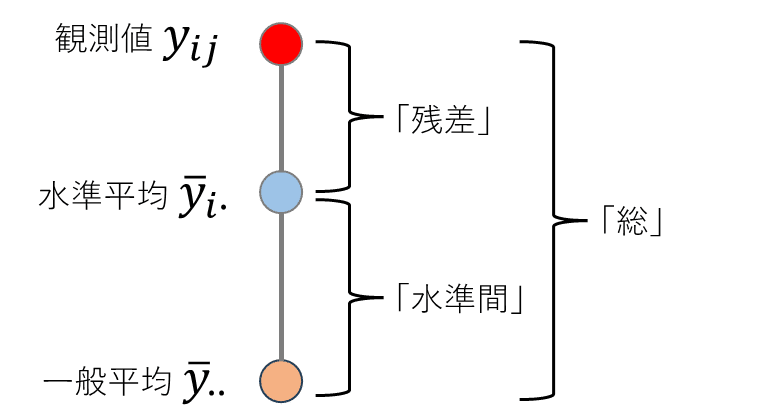
■ 「残差」「水準間」「総」の概念図
ざっくりですが、この図で残差と水準間の関係を確認します。

１．水準間平方和と残差平方和の数式

次の記号を用いて「水準間平方和」と「残差平方和」を「数式表現」します。

■ 水準間平方和の数式表現

水準間平方和は「（各水準の平均－一般平均）の二乗の和」です。
順を追って記号化・数式化していきましょう。

①各水準の平均は月ごとの平均なので、記号は$${\bar{y}_{i \cdot}}$$です。

②一般平均は全体の平均なので、記号は$${\bar{y}_{\cdot \cdot}}$$です。

③（各水準の平均－一般平均）の二乗は次のように書けます。
$${(\bar{y}_{i \cdot}-\bar{y}_{\cdot \cdot})^2}$$

④最後の「和」は２つに分けます。

まず、1ヶ月あたり11年分のデータがあります。
したがって、各月の③は11年分が必要になります。
③の数式をよく見ると、年$${j}$$がありません。
これはシンプルに11倍（11個足す）します。
$${11 \times (\bar{y}_{i \cdot}-\bar{y}_{\cdot \cdot})^2}$$

次に月ごとの$${11 \times (\bar{y}_{i \cdot}-\bar{y}_{\cdot \cdot})^2}$$を12ヶ月分、1月から12月まで足し上げます。
月によって値が異なりますので、総和記号$${\sum}$$の出番です。
月の記号$${i}$$をカウンタにして、1～12まで動かして足します。

$${S_A = \displaystyle \sum^{12}_{i=1} 11 \times (\bar{y}_{i \cdot}-\bar{y}_{\cdot \cdot})^2}$$

水準間平方和$${S_A}$$の数式が完成しました。
解答選択肢は ① か ② に絞り込まれました。

ちなみに、この問題の要因は「月」ですので、水準は各月となります。
したがって、水準間平方和の概念は「月」で構成され、「年」が入り込む余地はありません。
つまり、年ごとの平均値を持ち込んでいる解答選択肢 ③～⑤ はありえないということになります。

■ 残差平方和の数式表現

残差平方和は「（観測値－各水準の平均）の二乗の和」です。
順を追って記号化・数式化していきましょう。

①観測値は、売上高$${y_{ij}}$$です。

②各水準の平均は、月ごとの平均$${\bar{y}_{i \cdot}}$$です。

③（各水準の平均－一般平均）の二乗は次のように書けます。
$${(y_{ij}-\bar{y}_{i \cdot})^2}$$
※この時点で解答選択肢は１つに絞られます！

④最後の「和」は２つに分けます。

まず、1ヶ月あたり11年分のデータがあります。
したがって、各月の③は11年分が必要になります。
③の数式をよく見ると、年$${j}$$が含まれています。
年によって③の計算結果が異なるということです。
11年分を個別に足し上げる必要があります。
総和記号$${\sum}$$の出番です。
年の記号$${j}$$をカウンタにして、開始年2008年から終了年2018年まで足し上げます。
$${\displaystyle \sum^{2018}_{j=2008} (y_{ij}-\bar{y}_{i \cdot})^2}$$

次に月ごとの$${\displaystyle \sum^{2018}_{j=2008} (y_{ij}-\bar{y}_{i \cdot})^2}$$を12ヶ月分、足し上げます。
月によって値が異なりますので、総和記号$${\sum}$$の出番です。
月の記号$${i}$$をカウンタにして、1～12まで動かして足します。

$${S_e = \displaystyle \sum^{12}_{i=1} \displaystyle \sum^{2018}_{j=2008} (y_{ij}-\bar{y}_{i \cdot})^2}$$

残差平方和$${S_e}$$の数式が完成しました。
解答選択肢 ① が残りました。

この問題の解答選択肢は ① です。

■ おまけ：平方和の計算メカニズムから数式を解読する

「平方和の計算メカニズム」表を用いて、数式の中身を確認しましょう。
全体像は次のとおりです。

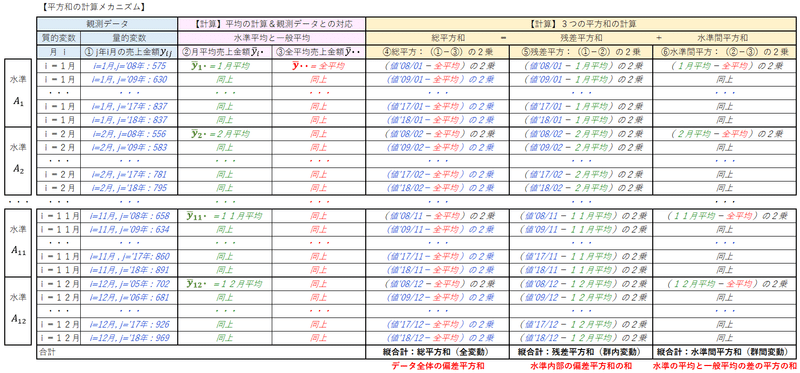
左側のゾーンにフォーカスします。
観測データ（売上データ）と関連する平均の表です。
個々の売上データは$${y_{ij}}$$、水準となる「月」の平均は$${\bar{y}_{i \cdot}}$$、全平均＝一般平均は$${\bar{y}_{\cdot \cdot}}$$です。
平方和はこの３つの役者が舞台に上がります。
つまり「年ごとの平均$${\bar{y}_{\cdot j}}$$は現れない」ということなのです。

続いて平方和に拡張しました。
左端の「⑥水準間平方」の欄を見てください。
１月の2005年～2018年の⑥水準間平方は同一の「（１月平均－全平均）の２乗」です。
これは「11×（１月平均－全平均）の２乗」なのです！
⑤残差平均は、１月の場合、「（値 j 年１月－１月平均）の２乗」です。
これは、１月について j 年としての2008年から2018年を足すことになり、総和記号$${\sum^{2018}_{j=2008}}$$が出動する事態になりました。

１月に注目して検討しました。
これを１月から１２月に拡張して足し上げるには、総和記号$${\sum^{12}_{i=1}}$$を用います。

２．分散分析表の自由度の穴埋め

「水準間」の自由度と「残差」の自由度を求めます。

■ 水準間の自由度

水準間の自由度は$${a-1}$$です。
$${a}$$は水準の数です。
本問題の水準は、1月から12月までの$${12}$$個です。
したがって、自由度は$${12-1=11}$$です。

■ 残差の自由度

残差の自由度は$${n-a}$$です。
$${n}$$は全体の標本サイズです。
本問題の標本サイズは、2008～2018年までの11年間の月数なので、$${11\times12=132}$$です。
したがって、自由度は$${132-12=120}$$です。

まとめます。
解答選択肢の（ア）水準間の自由度は$${11}$$、（イ）残差の自由度は$${120}$$です。

この問題の解答選択肢は ③ です。

■ おまけ：一元配置分散分析表のメカニズム

一元配置分散分析表は内部に足し算と割り算の関係を持っています。
この計算関係を次の図で確認しましょう。

３．分散分析表に基づく統計的仮説検定の結論文章の適否

３つの文章の適否を検討します。
３者の相違点＝３つの検討ポイントを並べます。
　①対立仮説は何か（記述Ⅰ vs Ⅱ・Ⅲ）
　②有意水準$${5\%}$$で棄却できるかどうか（記述Ⅰ vs Ⅱ）
　③$${p}$$値は$${2.5\%}$$未満であるか（記述Ⅲ）
順番に検討しましょう。

①対立仮説は何か？

一元配置分散分析の帰無仮説と対立仮説のまとめ図を見ましょう。

検定の視点２のパターンです。
・帰無仮説：「全ての水準の平均値は等しい」
・対立仮説：「どれかの水準の母平均は異なる」

では問題文の記述Ⅰから確認します。

これは適切ではありません。

これは適切です。

②有意水準$${\boldsymbol{5\%}}$$で棄却できるかどうか

$${F}$$分布のパーセント点表より、自由度$${(11, 120)}$$の$${F}$$分布の上側$${5\%}$$点を取得して、$${F}$$値$${3.0471}$$を比べます。

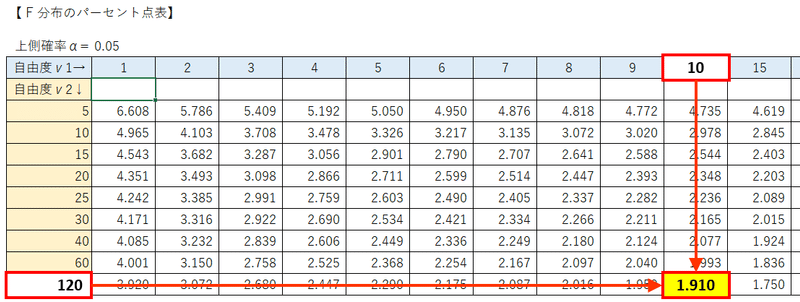
残念ですが、表の第１自由度に$${11}$$がありません。
統計的仮説検定では、$${5\%}$$よりも統計値（$${F}$$値）が大きい場合に棄却できます。
そこで、表の第１自由度の中で$${11}$$に近い$${10}$$と$${15}$$のパーセント点を比べて値の大きい方を採用します。
自由度$${11}$$のパーセント点$${1.910}$$の方が大きいので、この値と$${F}$$値$${3.0471}$$を比較します。
$${\boldsymbol{F}}$$値$${\boldsymbol{3.0471}}$$の方が大きいので、帰無仮説を棄却できます。

問題文の記述Ⅱを確認します。

この文章は、帰無仮説を棄却できないことを示しています。
したがって、記述Ⅱは適切ではありません。

③$${\boldsymbol{p}}$$値は$${\boldsymbol{2.5\%}}$$未満であるか

$${F}$$分布のパーセント点表より、自由度$${(11, 120)}$$の$${F}$$分布の上側$${2.5\%}$$点を取得します。
$${F}$$値$${3.0471}$$が上側$${2.5\%}$$点よりも大きい場合、$${p}$$値は$${2.5\%}$$より小さいです。

第１自由度は、パーセント点の値の大きい（より厳しく判定できる）$${10}$$を採用します。
自由度$${(11, 120)}$$の$${F}$$分布の上側$${2.5\%}$$点は$${2.157}$$です。
$${F}$$値$${3.0471}$$は、上側$${\boldsymbol{2.5\%}}$$点$${\boldsymbol{2.157}}$$よりも大きいので、$${\boldsymbol{p}}$$値は$${\boldsymbol{2.5\%}}$$より小さいと言えます。

問題文の記述Ⅲを確認します。

この文章は適切です。
したがって、記述Ⅲは適切です。

解答をまとめると「Ⅲのみ正しい」となります。
この問題の解答選択肢は ③ です。

自由度$${(11, 120)}$$の$${F}$$分布で$${F}$$値、上側$${5\%}$$点＆$${2.5\%}$$点を可視化して、大小関係を確かめましょう。

自由度$${(11, 120)}$$の$${F}$$分布の上側$${5\%}$$点は$${1.869}$$、上側$${2.5\%}$$点は$${2.102}$$、$${p}$$値は$${0.0013}$$でした。

最後に、一元配置分散分析表の完成イメージを記載します。

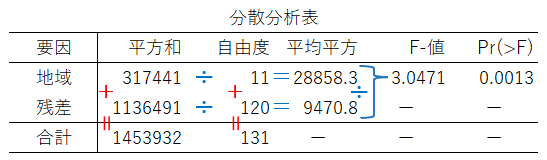
解答

〔1〕①、〔2〕③、〔3〕③ です。

難易度　やさしい

・知識：一元配置分散分析（平方和、自由度、仮説）、$${F}$$分布のパーセント点表
・計算力：数式組み立て（低）、電卓（低）
・時間目安：3問合計 5分

実践する

一元配置分散分析と時系列分析を実践する

問題集で利用されている「コンビニ売上高データ」を用いて一元配置分散分析を Python、手作業、EXCEL、R で実践しましょう！

そしてそして「コンビニ売上高データ」は、100ヶ月を超える「時系列」データです。
時系列分析に少々取り組みたいと思います。

■ 実践の流れ

１．Pythonで一元配置分散分析
　①問題集と同じ期間「2008年～2018年」
　②データの取得期間「2005年～2022年」
２．Pythonで時系列分析：「2005年～2022年」
３．手作業・EXCEL・Rで一元配置分散分析：「2008年～2018年」

Python 成分多めです！

■ 利用データの概要

日本フランチャイズチェーン協会様が公表する次の「コンビニエンスストア統計時系列データ」（pdfファイル）を利用しました。
・コンビニエンスストア統計時系列データ（2017年～2022年）
・コンビニエンスストア統計時系列データ（2005年～2016年）

データイメージです。

項目は、年、月、売上高（単位：10億円）で構成されています。
売上高は、引用元データの単位「100万円」を1000で割って、１の位で四捨五入しました。
なお、問題集には「単位：億円」と記載がありますが、おそらく誤植と思われます。

こちらが「一般社団法人日本フランチャイズチェーン協会（JFA）」様のサイトです。

こちらの「コンビニエンスストア統計データ」ページでデータ取得しました。

【出典記載】
「コンビニエンスストア統計時系列データ（2017年～2022年）」および「コンビニエンスストア統計時系列データ（2005年～2016年）」（一般社団法人日本フランチャイズチェーン協会）
（https://www.jfa-fc.or.jp/particle/320.html）

【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の資料を加工して作成しています。

CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
Pythonサンプルファイル、Rサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。

・「2008年～2018年」データ

・「2005年～2022年」年データ

Pythonで作成してみよう！

問題集の数値と照らし合わせながら【出力結果】をご確認ください。
プログラムがどうも…という方は、コード部分を読み飛ばして、表やグラフから時系列データの特徴を読み取ってみましょう！

１．一元配置分散分析：問題集と同じ期間「2008年～2018年」

① インポート

### インポート

# 数値計算
import numpy as np
import pandas as pd

# 統計処理
from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
import pingouin as pg

# 可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

② データの読み込み
項目「月」をcategory型にします。理由は後ほど。
また、「月」と「売上高」の項目を多用するので、変数 cat_col （月）、 target_col （売上高）で定数定義しました。

### データの読み込み

# csvファイルの読み込み
data = pd.read_csv(r'./sampledata.csv')

# 「月」をカテゴリ変数に変換
data['月'] = data['月'].astype('category')

# 説明変数cat_colと目的変数target_colの設定
cat_col = '月'
target_col = '売上高'

# データの表示
print('data.shape', data.shape)
display(data)
print(data.info())

【出力結果】

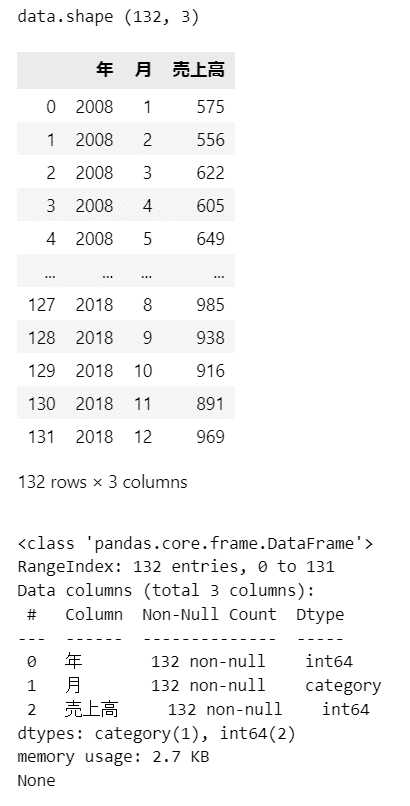
③ 行：「月」、列「年」のクロス集計表形式で表示
問題集に記載の「月／年別売上高表」を再現します。
pandas の pivot_table 関数で簡単に集計表形式にできます。

### 行：「月」、列「年」のクロス集計表形式で表示
data.pivot_table(index=cat_col, columns='年', values=target_col)

【出力結果】
数値の羅列は頭に入ってこないです・・・（苦笑）

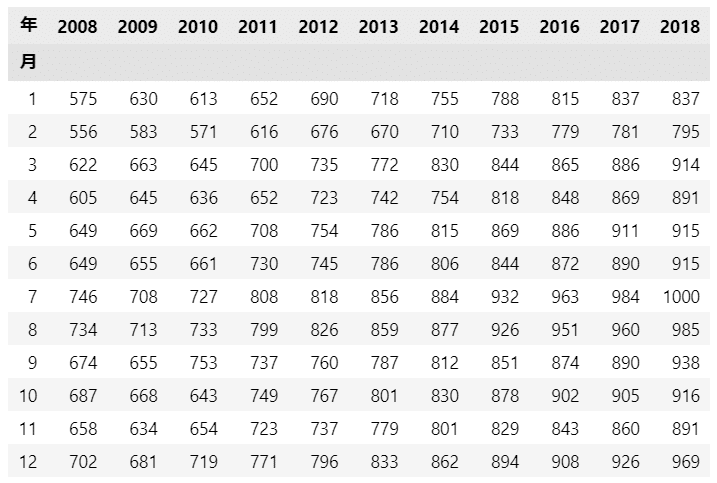
④ 月別の要約統計量
pandas の ピボットテーブル関数を用いて、月別の要約統計量をデータフレーム形式で作成します。
aggfunc 引数で統計量を指定します。

### カテゴリ別の要約統計量
pd.options.display.float_format = None
data.pivot_table(index=None, columns=cat_col, values=target_col,
                 aggfunc={target_col: [len, np.mean, np.std, min,np.median,
                                       max]},
                 sort=False).round(1)

【出力結果】

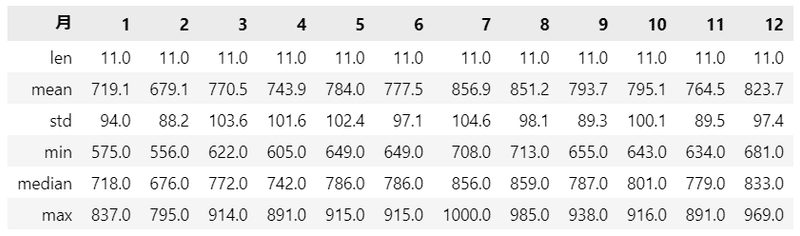
月が横に並んでいます。「mean」が平均です。
１年の中で、７、８月の平均売上高が高いです。

夏場のコンビニというと、アイス飲料、アイスクリーム、そば・うどん・冷やし中華などの冷たい麺、肌ケア（日焼け対策、ひんやりシートなど）が売れ筋なのでしょうか？
気になりました。

⑤ 箱ひげ図の描画
各月の売上高データのばらつきを箱ひげ図で確認しましょう。
seaborn の boxplot を利用します。

### 箱ひげ図の描画
sns.boxplot(x=cat_col, y=target_col, data=data);

【出力結果】

11年間の月データは、幅550～1000（単位：10億円）に収まります。
７、８月が売上高の上のピーク、２月が下のピークです。
毎月の「箱ひげ」の形はよく似ています。
12ヶ月サイクルの季節変動の傾向があるかもしれません。

⑥ 分散分析の実行
statsmodels、scipy.stats、pingouin の分散分析をコードを比べてみましょう（結果は同一です）。

■ statsmodels
回帰分析と同じように、ols（最小二乗法）に fit させてから、「anova_lm」で分散分析を実行します。
今回の平方和の桁数が大きいので、表示を見やすくするために、pandas の「pd.options.display.float_format」を設定しています。

### 分散分析 statsmodels
# df:自由度、sum_sq:平方和、mean_sq:平均平方、F:F値、PR(>F):上側片側確率のp値

# データフレームの表示桁数の設定
pd.options.display.float_format = '{:.4f}'.format

# モデルの定義・フィット
anova = smf.ols('売上高 ~ 月', data=data).fit()

# 分散分析の実行
result_sm = sm.stats.anova_lm(anova, typ=1)
result_sm

【出力結果】

【統計的仮説検定の結論】
$${p}$$値（PR(＞F)）の値は$${0.0013}$$であり、有意水準$${5\%}$$よりも小さいです。
したがって、有意水準$${5\%}$$で帰無仮説は棄却され、対立仮説「少なくとも１つの月は他の月と母平均が異なる」と言えます。

【statsmodelsの使い勝手】
問題集の掲載、および、この記事の「問題を解きながら知る」の章で作成した一元配置分散分析表と同じ値が得られました。
データがあればサクッと一元配置分散分析できる点がプログラミング言語利用のよいところです。

【statsmodelsの特質】
「② データの読み込み」で項目「月」をcategory型にしたのは、statsmodelsで処理できるようにするためです。
「月」を数値型にして実行したところ、statsmodelsは「量的変数」と判断するようで、うまく処理できませんでした。
category型にしたところ、statsmodelsは「質的変数」と判断できたようです。

■ scipy.stats
一元配置分散分析用の関数 f_oneway を利用します。
この関数は、引数に「水準別」（月別）に分けられたデータを指定する必要があります。
そこで、コードの前段で、水準別データを作成しています。
pandas の groupby を使って、月別にデータを格納する「data_by_category」を作成しています。

### 分散分析 scipy.stats

# GroupByオブジェクトの生成
groups = data.groupby(cat_col, sort=False)

# 水準別データの作成
data_by_category = []
for category in list(groups.groups):
    data_by_category.append(groups.get_group(category)[target_col])

# 分析分析の実行＆データフレームに格納
result_stats = pd.DataFrame(columns=['F値', 'p値'])
result_stats.loc[cat_col] = stats.f_oneway(*data_by_category)
result_stats.round(4)

【出力結果】

f_oneway 関数の出力は$${F}$$値と$${p}$$値の２項目です。
取り急ぎ「３つ以上のグループの母平均の差の検定をしたい」という場合に利用する感じでしょう。

■ pingouin
anova 関数の１行だけで分散分析を行なえます。
一番シンプルなコードだと思います。
引数は、dv:目的変数（従属変数）、between:水準を含む変数（水準間）などです。

### 分散分析 pingouin
## Source:要因、SS:平方和、DF:自由度、MS:平均平方、F:F値、P-unc:p値、np2：相関比

result_pg = pg.anova(dv=target_col, between=cat_col, data=data, detailed=True)
result_pg

【出力結果】

一元配置分散分析の「水準間」「残差」（水準内：Within）行が表示されました。
分散分析表の項目が網羅されています。
そして、相関比$${\eta^2}$$（np2）の表示もあります。
相関比は、質的変数と量的変数の相関関係にかかわる統計量です。
「水準間平方和÷総平方和」で計算できます。
なお、pingouinは「月」が数値型の場合も、正しく処理できました。

⑦ 各水準の信頼区間の描画
各月の母平均の信頼区間をグラフに描画します。
思いの外、長いコードになりました。

■ 計算要素の算出

### 信頼区間の計算要素の算出

# 設定 信頼係数
cf = 0.95

# 計算要素の算出
df = result_sm.df.Residual                     # 残差の自由度
mean_square = result_sm.mean_sq.Residual       # 残差の平均平方
t_ppf = stats.t.ppf((1 + cf) / 2, df)          # t分布の上側cf/2％点
counts = groups[[target_col]].count()          # 各水準のデータ数
means = groups[[target_col]].mean()            # 各水準の平均値

# 信頼区間の片幅（正値側）の算出
ci_upper = t_ppf * np.sqrt(mean_square / counts)

# 計算要素の表示
print(f't分布の上側{(1-cf)/2:.1%}: {t_ppf:.3f}, 残差の平均平方: {mean_square:.3f}, '
      f'信頼区間の片幅（正値側）: {ci_upper.iloc[0, 0]:.3f}')

【出力結果】

■ 信頼区間の表示
pandas のデータフレーム形式に加工するので、コードが増えました。

### 水準別の信頼区間の表示

# 下端の設定
groups_ci = (means - ci_upper).rename(columns={target_col: '下端'})
# 平均の設定
groups_ci['平均'] = means
# 上端の設定
groups_ci['上端'] = means + ci_upper
# 表示
pd.options.display.float_format = None
groups_ci.T.round(2)

【出力結果】

■ グラフ描画
matplotlib の errorbar 関数を利用します。
信頼区間の片側の値を引数「yerr」に渡します。

### エラーバー付きプロットの描画

# エラーバー付きプロットの描画
plt.errorbar(means.index, means[target_col], yerr=ci_upper[target_col],
             marker='o', markersize=15, linewidth=0, elinewidth=1,
             ecolor='gray', capsize=10)
# 修飾
plt.xlim(0, 13)
plt.title('月別売上高 母平均の95%信頼区間')
plt.xlabel('月')
plt.ylabel('売上高（10億円）')
plt.show()

【出力結果】

母平均の平均の95%信頼区間は、ヒゲの上下の範囲です。
ヒゲの長さは、片側 58.096 （単位：10億円）です。

以上で2008～2018年のデータの一元配置分散分析を終了いたします。

２．一元配置分散分析：「2005～2022年」

データの期間が前後に延びて、2005年～2022年の18年間、216ヶ月のデータで「月別平均の行方」を確認しましょう。

① データの読み込み
sampledata2.csv を読み込みます

### データの読み込み

# csvファイルの読み込み
data2 = pd.read_csv(r'sampledata2.csv')

# 「月」をカテゴリ変数に変換
data2['月'] = data2['月'].astype('category')

# 説明変数cat_colと目的変数target_colの設定
cat_col = '月'
target_col = '売上高'

# データの表示
print('data2.shape', data2.shape)
display(data2)
print(data2.info())

【出力結果】

② 月別の要約統計量

### 月別の要約統計量
# pd.options.display.float_format = None
data2.pivot_table(index=None, columns=cat_col, values=target_col,
                  aggfunc={target_col: [len, np.mean, np.std, min, np.median,
                                        max]},
                 sort=False).round(1)

【出力結果】
「2008年～2018年データ」と比べると、平均値が増えている月、減っている月があります。

③ 箱ひげ図の描画

### 箱ひげ図の描画
sns.boxplot(x=cat_col, y=target_col, data=data2);

【出力結果】
７、８、１２月の売上高が1000（単位：10億円）を超えてきました。
ヒゲの上端が 1000 を超えています！

④ 分散分析の実行
statsmodels、scipy.stats、pingouin の分散分析をコードを比べてみましょう（結果は同一です）。

■ statsmodels

### 分散分析 statsmodels
# df:自由度、sum_sq:平方和、mean_sq:平均平方、F:F値、PR(>F):上側片側確率のp値

# データフレームの表示桁数の設定
pd.options.display.float_format = '{:.4f}'.format

# モデルの定義・フィット
anova2 = smf.ols('売上高 ~ 月', data=data2).fit()

# 分散分析の実行
result_sm2 = sm.stats.anova_lm(anova2, typ=1)
result_sm2

【出力結果】

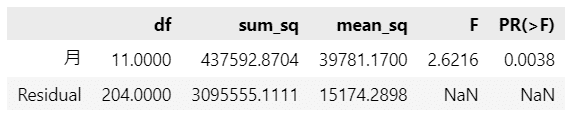
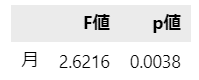
「2008年～2018年データ」と比べると、$${F}$$値の値が小さくなり、$${p}$$値の値が大きくなりました。

【統計的仮説検定の結論】
$${p}$$値（PR(＞F)）の値は$${0.0038}$$であり、有意水準$${5\%}$$よりも小さいです。
したがって、有意水準$${5\%}$$で帰無仮説は棄却され、対立仮説「少なくとも１つの月は他の月と母平均が異なる」と言えます。

■ scipy.stats

### 分散分析 scipy.stats

# GroupByオブジェクトの生成
groups2 = data2.groupby(cat_col, sort=False)

# 水準別データの作成
data_by_category2 = []
for category2 in list(groups2.groups):
    data_by_category2.append(groups2.get_group(category2)[target_col])

# 分析分析の実行＆データフレームに格納
result_stats2 = pd.DataFrame(columns=['F値', 'p値'])
result_stats2.loc[cat_col] = stats.f_oneway(*data_by_category2)
result_stats2.round(4)

【出力結果】

■ pingouin

### 分散分析 pingouin
## Source:要因、SS:平方和、DF:自由度、MS:平均平方、F:F値、P-unc:p値、np2：相関比

result_pg2 = pg.anova(dv=target_col, between=cat_col, data=data2, detailed=True)
result_pg2

【出力結果】

⑤ 各水準の信頼区間の描画

■ 計算要素の算出

### 信頼区間の計算要素の算出

# 設定 信頼係数
cf2 = 0.95

# 計算要素の算出
df2 = result_sm2.df.Residual                     # 残差の自由度
mean_square2 = result_sm2.mean_sq.Residual       # 残差の平均平方
t_ppf2 = stats.t.ppf((1 + cf2) / 2, df2)         # t分布の上側cf/2％点
counts2 = groups2[[target_col]].count()          # 各水準のデータ数
means2 = groups2[[target_col]].mean()            # 各水準の平均値

# 信頼区間の片幅（正値側）の算出
ci_upper2 = t_ppf2 * np.sqrt(mean_square2 / counts2)

# 計算要素の表示
print(f't分布の上側{(1-cf2)/2:.1%}: {t_ppf2:.3f}, '
      f'残差の平均平方: {mean_square2:.3f}, '
      f'信頼区間の片幅（正値側）: {ci_upper2.iloc[0, 0]:.3f}')

【出力結果】

■ 信頼区間の表示

### 水準別の信頼区間の表示

# 下端の設定
groups_ci2 = (means2 - ci_upper2).rename(columns={target_col: '下端'})
# 平均の設定
groups_ci2['平均'] = means2
# 上端の設定
groups_ci2['上端'] = means2 + ci_upper2
# 表示
pd.options.display.float_format = None
groups_ci2.T.round(2)

【出力結果】

■ グラフ描画

### エラーバー付きプロットの描画

# エラーバー付きプロットの描画
plt.errorbar(means2.index, means2[target_col], yerr=ci_upper2[target_col],
             marker='o', markersize=15, linewidth=0, elinewidth=1,
             ecolor='gray', capsize=10)
# 修飾
plt.xlim(0 ,13)
plt.title('月別売上高 母平均の95%信頼区間')
plt.xlabel('月')
plt.ylabel('売上高（億円）')
plt.show()

【出力結果】
「2008年～2018年」データと比べると、８月が伸びて７月を超えました。
真夏の売れ筋がとても気になります！

以上で一元配置分散分析のコードは完了です。
月平均をとり、月別の売上の平均に差があることを知っておくことは、スタッフやお金のやりくりの観点で、なにか示唆を得ることができるかもです。
しかし、一元配置分散分析では「◯月が明確に差がある」と言う結論を出せないので、なんだかもどかしいです。

このもやもやを「時系列分析」にぶつけてみましょう。

３．時系列グラフのプロット：「2005年～2022年」

まず、コンビニ売上高の時系列グラフを描画して、変動の傾向を確認します。

① 時系列プロット関連ライブラリのインポート
statsmodelsの時系列ライブラリを利用します。

### 時系列プロット関連ライブラリのインポート
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

② データフレームの日付をインデックス化
データを時系列ライブラリで使いやすくする目的で、年月の項目をデータフレームのindexに設定します。

### 年月を日付index化
data3 = data2.copy()
data3.index = pd.to_datetime(data3['年'].astype(str) + '-' \
                             + data3['月'].astype(str).str.zfill(2))
data3 = data3.drop(['年', '月'], axis=1)
display(data3)

【出力結果】

③ 時系列グラフの描画
時系列の売上高の推移を描画しましょう。

### 時系列グラフの描画
fig, ax = plt.subplots(figsize=(8, 3))
data3[target_col].plot(ax=ax,
                       title='コンビニ売上高推移（単位：億円）：2005～2022年');

【出力結果】

右肩上がりの傾向と、１年サイクルの上下変動が見られます。
また、2019年～2020年ごろに下降傾向が見られます。
新型ウィルスの影響でしょうか。
変化点を詳しく見てみましょう。

④ 変化点の推測
ruptures ライブラリを用いて、コンビニ売上高の傾向に変化が見られる点を検出します。

■ インポート

### 変化点検出ライブラリのインポート
## インストール
## conda install -c conda-forge ruptures
## pip install ruptures

import ruptures as rpt

■ 変化月の推測
１行目のコードで変化点を検出して、結果を result_rpt に格納しています。
３行目のコードで変化点を可視化しています。

### 変化月の推測

# 変化点を推測　アルゴリズム：PERT、損失関数：rbf
result_rpt = rpt.Pelt(model='rbf').fit(data3).predict(pen=1)

# 変化月を表示
print('【変化年月】\n', data3.index[np.array(result_rpt)-1].astype(str))

# グラフ表示
rpt.show.display(data3, (0, 0), result_rpt, figsize=(8, 3));

【出力結果】

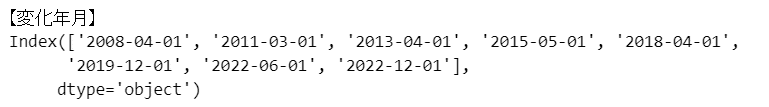
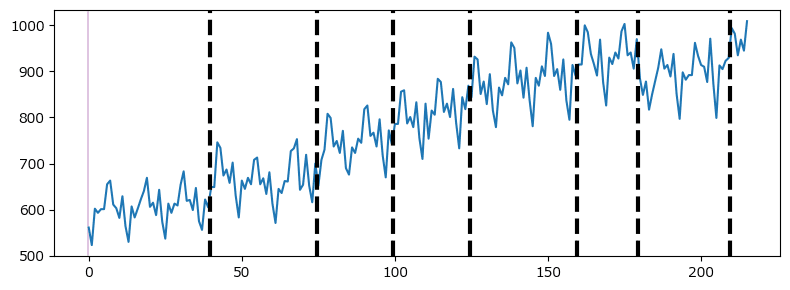
検出した変化年月は８点です。
８つの潮目。
社会的な出来事や景気動向に思い当たることはあるでしょうか。
・2008年4月
・2011年3月
・2013年4月
・2015年5月
・2018年4月
・2019年12月
・2022年6月
・2022年12月

⑤ 変動分解グラフの描画
時系列の波を、長期のトレンド成分、季節変動の成分、不規則変動成分に分解してグラフにします。

### 変動分解グラフの描画

# 変動分解実行（移動平均による加法モデル）
result = seasonal_decompose(data3[target_col], model='additive', period=12)

# 変動分解グラフの描画
fig = result.plot()
fig.set_size_inches((8, 10));

【出力結果】

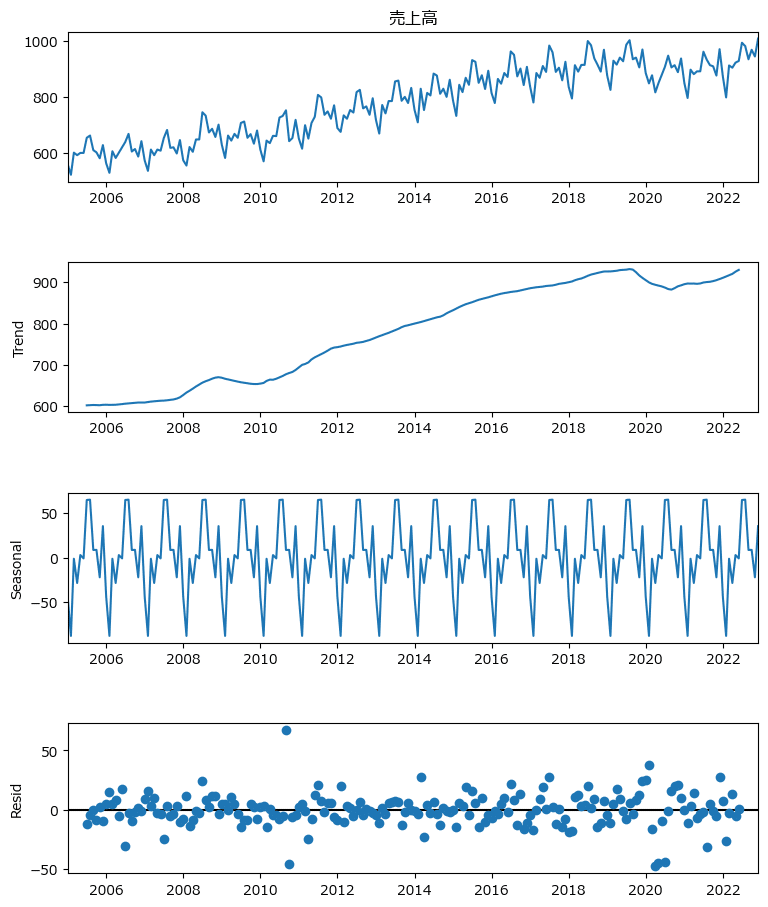
２番目の「Trend」（トレンド）では、2019年あたりまで右肩上がりの上昇があり、その後、数カ月間は下落し、再度、緩やかな上昇が見られます。
３番目の「Seasonal」（季節変動）では、きれいに１年サイクル（12ヶ月サイクル）が見られます。
箱ひげ図や信頼区間のグラフで見た「月の上下」が季節変動の形で明確に分かりました。

⑥ コレログラム、偏自己相関係数のグラフ描画

### コレログラム、偏自己相関係数のグラフ描画
## 設定：ラグ
lags = 50

## 描画
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(7, 5), sharex=True, sharey=True)
# コレログラムの描画
ax1 = plot_acf(data3[target_col], lags=lags, ax=ax1)
# 偏自己相関係数の描画
ax2 = plot_pacf(data3[target_col], lags=lags, ax=ax2, method='ywm')

plt.tight_layout()
plt.show()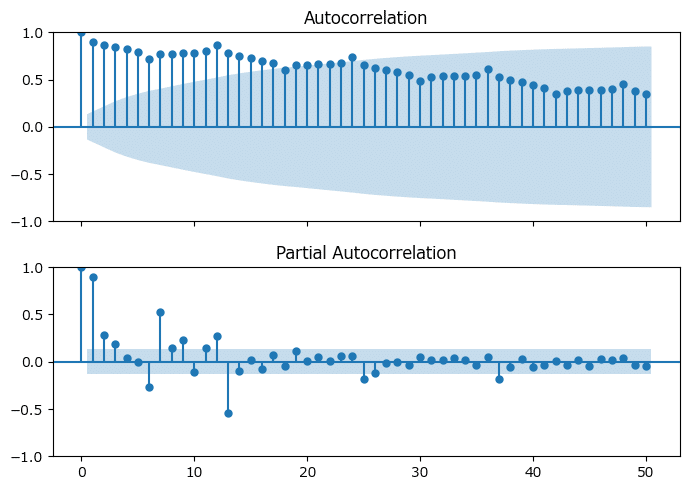

上のコレログラムは非常にゆっくりと減衰しています。
下の偏自己相関係数はラグ１、７，１３が少し高い感じがします。

季節変動があり、一定傾向のトレンドがあるなど、時系列の流れ・波がありそうです。
次のステップは、時系列モデルを構築して流れ・波をつかみ、コンビニ売上高の予測をしてみましょう。

４．時系列モデルの分析

季節成分を加味した時系列モデル SARIMA でザックリ時系列モデルを構築して、未来を予測しましょう！

① 時系列モデル分析ライブラリのインポート

自動で最適な時系列モデルを探索するライブラリ pdmarima を利用します。

### 時系列モデル分析ライブラリのインポート

# 時系列モジュール
from pmdarima import auto_arima

# 評価用モジュール
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_absolute_percentage_error

② 最適なSARIMAモデルの探索
１行のコードで最適なモデルを探索できます！
季節成分は 12ヶ月を指定します。

### 最適なSARIMAモデルの探索
arima_result = auto_arima(data3, seasonal=True, m=12, trace=False)
display(arima_result.summary())

【出力結果】

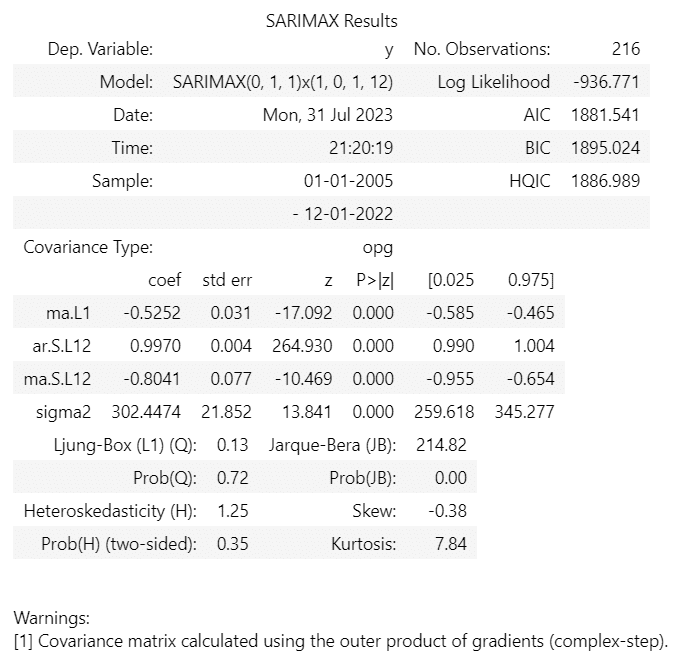
最適なモデルは、SARIMA(0, 1, 1)(1, 0, 1)[12] のようです。

このモデルを使って、コンビニ売上高の近未来「2023年1月～12月」を予測してみましょう！

③ 予測の実行
１行目のコードは、実績期間2005年～2022年を対象にして、モデルで予測したときの予測値を算出しています。
３行目のコードは、実績データの期間外（未知）である2023年1月～12月の予測値と95%信頼区間を算出しています。

### 予測の実行

# 実績データに対する予測
data3_pred = arima_result.fittedvalues()

# 将来の予測（2023年1～12月の12ヶ月）
n_periods = 12
future_pred, cf_interval = arima_result.predict(n_periods=n_periods,
                                                return_conf_int=True,
                                                alpha=0.05)

④ 予測データのグラフ描画
グラフを作成します！
結果が楽しみですね！！

# 予測データのグラフ描画

### 初期値設定
# 2023年1月からの12ヶ月の日付データ
future_months = [np.datetime64(f'2023-{i+1:02}-01') for i in range(n_periods)]
# 全年月データ（2005年1月～2023年12月）
all_months = np.hstack((data3.index, future_months))
# 全年月の予測値
all_predict = np.hstack((data3_pred, future_pred))

### 描画
plt.figure(figsize=(10, 6))

## グラフの描画
# 実績値（～2022年12月）
plt.plot(data3.index, data3[target_col], color='steelblue', label='実績')
# 予測値（～2023年12月）
plt.plot(all_months, all_predict, color='red', ls='--', label='予測')
# 2023年1月の垂直線
plt.axvline(np.datetime64(f'2023-01-01'), color='gray', ls=':')

# 修飾
plt.ylim(500, 1100)
plt.xlabel('年月')
plt.ylabel('売上高（単位：10億円）')
plt.legend(fontsize=12)

plt.show()

【出力結果】
青線が実績値、赤い点線が予測値です。
2022年12月までの実績値と予測値はよく似た動きをしています。
ほどよく予測できている感じです！

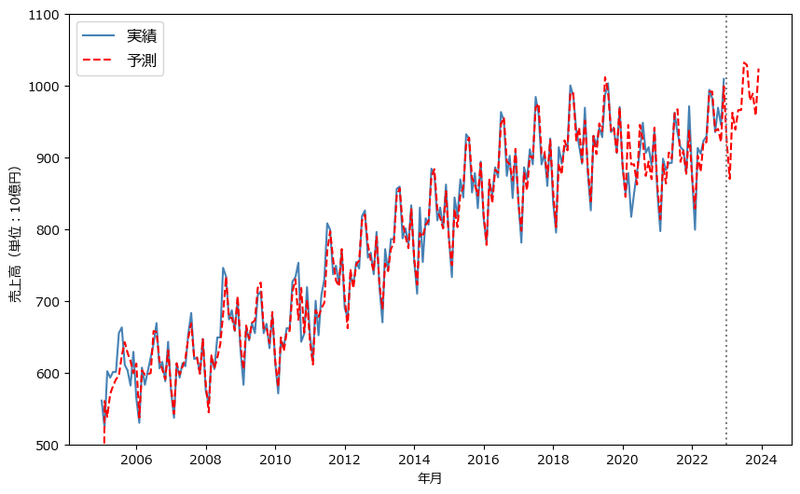
実は、執筆時点で2023年1月～6月のコンビニ売上高が公表されています。
この正解値（実績値）と予測値をプロットして答え合わせしてみましょう。

⑤ 2022年～2023年の予測値と実績値のグラフ描画
まず、2023年1月～6月のデータを設定します。
出典は次のとおりです。

【出典記載】
「ＪＦＡコンビニエンスストア統計調査月報 2023年1月度～6月度」
（一般社団法人日本フランチャイズチェーン協会）
（https://www.jfa-fc.or.jp/particle/320.html）

【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の資料を加工して作成しています。

### 2023年1～6月の全店売上高デーアの登録
### 引用元：ＪＦＡコンビニエンスストア統計調査月報 2023年1月度～6月度
### https://www.jfa-fc.or.jp/particle/320.html

data2023 = np.array([908476, 848100, 967117, 952072, 973580, 962275])
data2023 = (data2023/1000).round(0)

続いて、グラフを描画します。
範囲は2022年～2023年の２年に絞り込みます。

# 予測データのグラフ描画

# 全年月の実績値（～2023年6月）
all_actual = np.hstack((data3[target_col], data2023))

plt.figure(figsize=(10, 6))

### グラフの描画
# 実績値2022年1月～2023年6月）
plt.plot(all_months[-24:-6], all_actual[-18:], color='steelblue', label='実績')
# 予測値2022年1月～2023年12月）
plt.plot(all_months[-24:], all_predict[-24:], color='red', ls='--', label='予測')
# 予測値の95%信頼区間
plt.fill_between(all_months[-13:],
                 np.hstack((all_predict[-13], cf_interval[:, 0])),
                 np.hstack((all_predict[-13], cf_interval[:, 1])),
                 color='tomato', alpha=0.2, label='95%信頼区間')
# 2023年1月の垂直線
plt.axvline(np.datetime64(f'2023-01-01'), color='gray', ls=':')

# 修飾
plt.ylim(700, 1100)
plt.xlabel('年月', fontsize=14)
plt.ylabel('売上高（単位：10億円）', fontsize=14)
plt.legend(loc='upper left', fontsize=14)

plt.show()

【出力結果】
いい感じに予測できているのでは！！！

2023年1月の垂直点線から右側が2023年の予測値（赤点線）と実績値（青線）です。
予測値はかなり実績値に近い感じがします。
もしも、この予測値の精度が高いならば、2023年7月以降の売上高は前年を上回る可能性があります！
なお、薄い赤色で塗られた面は、予測値の95%信頼区間です。

⑥ 予測精度の確認
全期間（2005年1月～2023年6月）の予測精度の評価値は次のとおりです。

### 2005年1月～2023年6月の間の実績値と予測値の評価

print(f'MAE = {mean_absolute_error(all_actual, all_predict[:-6]):8.4f}')
print(f'RMSE= {np.sqrt(mean_squared_error(all_actual, all_predict[:-6])):8.4f}')
print(f'MAPE= {mean_absolute_percentage_error(all_actual, all_predict[:-6]):8.4f}')

【出力結果】

2023年1月～6月の予測精度の評価値は次のとおりです。

### 2023年1～6月の間の実績値と予測値の評価
print(f'MAE = {mean_absolute_error(data2023, future_pred[:6]):8.4f}')
print(f'RMSE= {np.sqrt(mean_squared_error(data2023, future_pred[:6])):8.4f}')
print(f'MAPE= {mean_absolute_percentage_error(data2023, future_pred[:6]):8.4f}')

【出力結果】

今年の7月以降の売上高が気になりました。
過去最高値を記録できるでしょうか？

Pythonを活用して、一元配置分散分析から時系列分析まで、とても楽しく学ぶことができました。
データをいろんな側面から眺めて、分析して、結果や予測を楽しめるのは、なんだか幸せです🍀

【謝辞】
時系列分析のコードは次の書籍を参考にしました。
ありがとうございます！

「Pythonによる時系列分析: 予測モデル構築と企業事例」

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

手作業で作成してみよう！

「2008年～2018年」のコンビニ売上高データを用いて、一元配置分散分析を実践しましょう。
問題集の数値と照らし合わせながら、数値作りを楽しみましょうね！

① 平方和の算出

さっそく「平方和の計算メカニズム」表を埋めていきます！
まず左側のゾーンです。
青い項目は、コンビニ売上高データを「質的変数」と「量的変数」に区分して整理し直しました。
ピンクの項目は、②が月別平均です。
③は、全データの平均＝一般平均です。
132ヶ月分のデータを縦に並べると「長い表」が出来上がります。

続いて右側のゾーンに計算を進めます。

黄色の項目が増えました。
④は「（①売上高－③全平均）の２乗」の数値です。
⑤は「（①売上高－②月別平均）の２乗」の数値です。
⑥は「（②月別平均－③全平均）の２乗」の数値です。

長いです！
④～⑥の縦合計が平方和のゴールです。
左から「総平方和」「残差平方和」「水準間平方和」です。
この３つの平方和を「分散分析表」に持ち込みます！

② 分散分析表の計算

一元配置分散分析表のメカニズムを振り返ります。
「水準間平方和」と「残差平方和」を分散分析表の左の列に転記します。

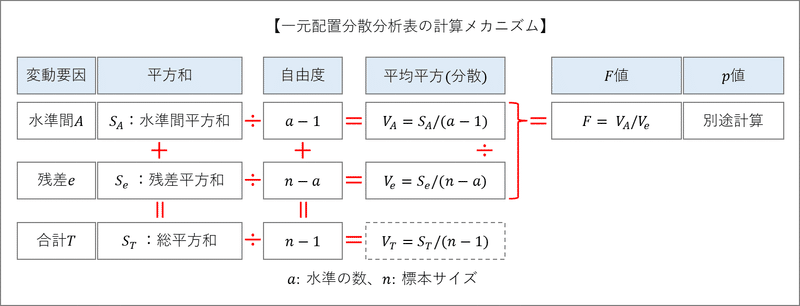
自由度は計算メカニズムの数式どおりに計算して値を記入します。
その後、足し算と割り算を計算して、各欄を埋めます。

完成イメージは次のようになります。

要因「月」と「残差」の横に向かって「平方和÷自由度＝平均平方」を計算しましょう。
最後に「月の平均平方÷残差の平均平方＝F値」を計算しましょう。

さて、p値はどうやって計算するのでしょう・・・
（Excelの関数を使いました）

③ 統計的仮説検定の結論

月の売上高平均に差はあるかを知りたいのでした。
帰無仮説は「各月の売上高の母平均は等しい」です。
$${p}$$値の計算が煩雑なことを踏まえて、$${F}$$分布のパーセント点を用いて棄却域を算出しましょう。

検定の方法は「上側確率」の片側検定です。
有意水準は$${5\%}$$に設定しました。
自由度$${(11,120)}$$の上側$${5\%}$$点を取得して、$${F}$$値と比べることにしましょう。

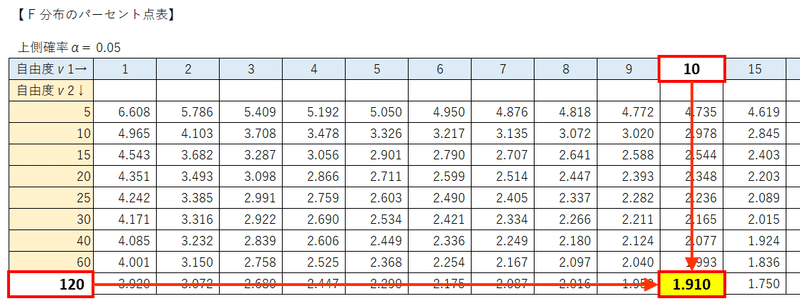
第２自由度の欄に「11」が無いので、代用として「10」を利用します。
かなりザックリしていますのでご容赦くださいな🌺

自由度$${(10,120)}$$の上側$${5\%}$$点は$${1.910}$$です。
$${F}$$値$${3.0471}$$は上側$${5\%}$$点$${1.910}$$よりも大きいので、棄却域に含まれます。

【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、対立仮説「月のどれかの母平均は他の月と異なる」と言えます。

自由度$${(11,120)}$$の$${F}$$分布で上側$${5\%}$$点と$${F}$$値の位置関係を確かめましょう。

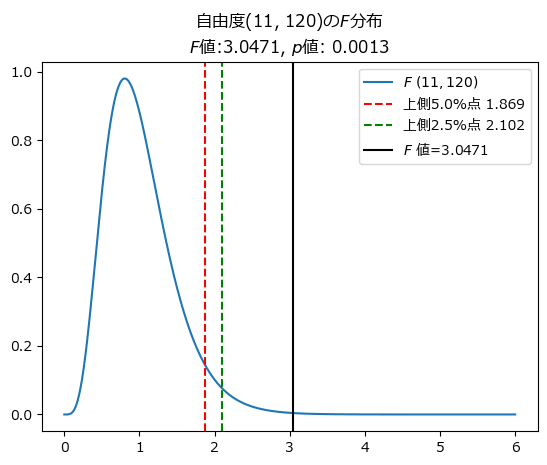
確かに、$${F}$$値（黒線）は上側$${5\%}$$点（赤点線）の上側、つまり棄却域に位置しています。

EXCELで作成してみよう！

データ分析機能の「分散分析－一元配置」を利用して、サクッと一元配置分散分析を実施しましょう。

データの外観
データは年・月ごとに行が別れている「縦持ち」の形式です。

「分散分析－一元配置」では、月別に売上高データが横並びする「横持ち」の形式を求めています。
さて、データをどう料理しましょう？

ピボットテーブルで横持ちに

ピボットテーブルで下図のように、縦に月が並び、横に年が並ぶクロス集計表の形式に変換できます。

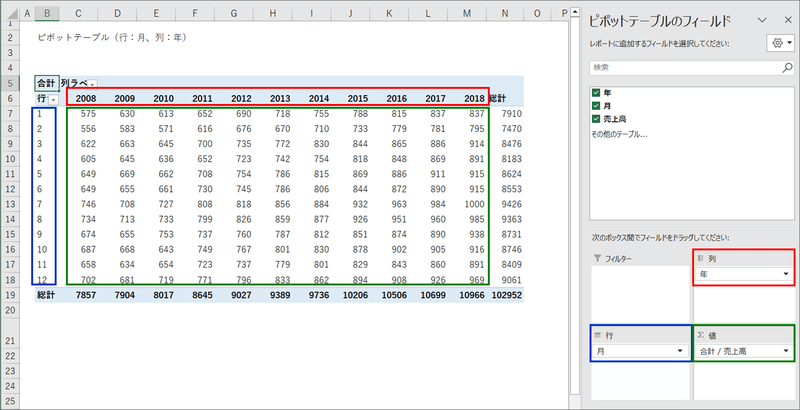
これで、一元配置分散分析の機能を使えます！

一元配置分散分析表の作成

メニューより、「データ」＞「データ分析」を指定して、「データ分析」画面を開き、「分散分析：一元配置」を指定して「ＯＫ」ボタンをクリックします。

入力範囲に先程のピボットテーブルを指定します。
データ方向は「行」です。
「ＯＫ」ボタンをクリックすると、分散分析表が表示されます。

一元配置分散分析表の確認

EXCEL画面に一元配置分散分析表が表示されました。
上段に「月」別の基本統計量、下段に分散分析表です。

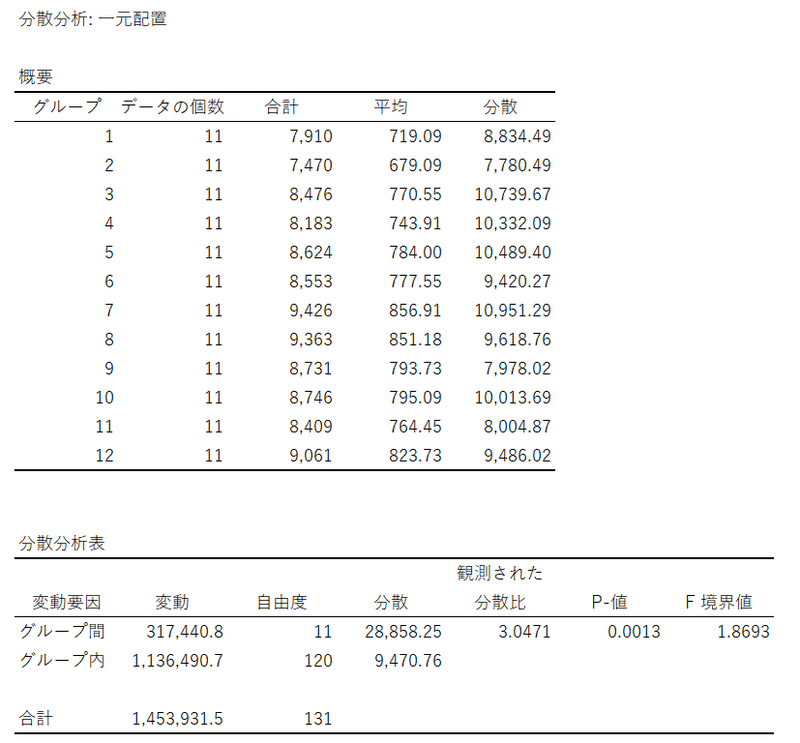
下段に注目しましょう。
グループ間（水準間）は、「月」の間の平方和（変動）、平均平方（分散）です。
グループ内（水準内）は、残差の平方和（変動）、平均平方（分散）です。
$${F}$$値（観測された分散比）は$${3.0471}$$、$${p}$$値は$${0.0013}$$。

統計的仮説検定

有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値は有意水準より小さいので、帰無仮説を棄却できます。

【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、対立仮説「月のどれかの母平均は他の月と異なる」と言えます。

まとめ

かなりシンプルな操作で本格的な分散分析表を作成できました。
（手作業と比べてみてください！）
ぜひぜひ、３種類以上のグループのデータ平均を比べてみましょう！

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

R で作成してみよう！

R スクリプトで一元配置分散分析を実践します。
コードはめっちゃシンプルです。

① データの読み込み
「月」を「要因型」に変換します。
「数値型」のまま分散分析を実施すると、適切な結果を得られないからです。

### データの読み込み
data <- read.csv('sampledata.csv')
# 月を要因型に変換
data$月 <- factor(data$月)
# データの要約表示
str(data)
summary(data)

【出力結果】
データは変数「年」「月」「売上高」で構成されます。
「月」は「factor」（要因型）です。

② 月別の統計量の表示
psych ライブラリの describeBy 関数を利用します。

### 月別の統計量
library(psych)
describeBy(data$売上高, data$月)

【出力結果】
12ヶ月分の基本統計量が表示されました。
各月について、データの数（n）、平均（mean）、標準平均（sd）、中央値（median）、最小値（min）、最大値（max）などを確認できます。

水準の数が多いと、このような統計量の確認作業が大変になります。

③ 箱ひげ図の描画
箱ひげ図で月ごとのデータの外観を確認しましょう。

### 箱ひげ図グラフ
boxplot(売上高~月, data=data, 
        main='コンビニ売上高 2008～2018年（単位:10億円）', 
        col=c('lightpink', 'lightgreen', 'lightblue'))

【出力結果】
夏の売上高の値が大きいことを見つめるうちに、真夏の大冒険～！のフレーズを思い出しました。
もう２年経ったのですね。肉眼で観戦したかったです。

④ 分散分析の実行
真打ちの登場です。
たった１行で分散分析ができます！

### 分散分析の実施と結果表示
anova(aov(売上高 ~ 月, data=data))

【処理結果】

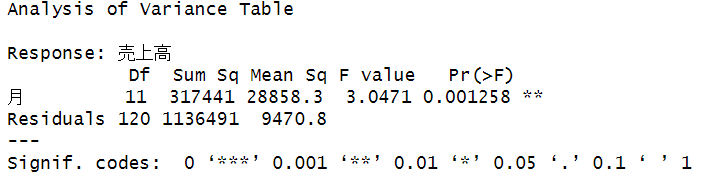
$${p}$$値（Pr(>F)）の表示があるので、検定の結論を出しやすいです。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値は有意水準より小さいので、帰無仮説を棄却できます。

【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、対立仮説「月のどれかの母平均は他の月と異なる」と言えます。

まとめ

R のコードは非常にシンプルです。
シンプル・イズ・ベストな方にお勧めいたします。

Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイルをダウンロードできます。

以上で本記事の一元配置分散分析を完了いたします。
長旅、お疲れ様でした。
最後までお付き合いしてくださり、ありがとうございました。

おわりに

月ごとに売上高の平均が異なるか、という視点はなかなか面白いです。
分散分析から出発して、時系列グラフを確かめて、将来の売上高を予測するところまで到達することができました。
お手元にデータがありましたら、「どう料理してみようか？」「あの切り口でデータを分析するとどうなるだろうか？」などのように、
　疑問（Problem）→分析（Analyze）→納得（Insight）→行動（Action）
のサイクルを回せると楽しくなります、きっと！
（パパイア・フレームワークより）

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次