一週間ほど前に投稿したno+e感想文に普段よりも多くの反応がありました。読んでくださった方々に感謝します（短編小説「蜘蛛姉」の方もよろしくお願いします。小説の方は、繰り返し読んでいただけると幸いです）。

そして、すたりむ さんが私の記事を引用してくださいました。

なので、今日は数学の話を書きます。私のno+eの読者は数学が苦手（というか嫌い）な人が半数以上な感じですが、この話のオチは「数学では『定義すること』は非常に難しい問題である」に繋がるので、そこだけ伝われば満足です。

また、上で紹介した記事の中で すたりむ さんが、

と述べておられますが、その点について反論するつもりもありません。良く紹介される円周率の定義を私は嫌っているけれど、『解析入門Ｉ』の円周率の定義に至るまでの議論は気に入っている、というのが私の感覚です。

とにかく、今日はすたりむさんの引用を受けて、円周率の定義の話をしようと思います。

「(円周率):=(円周の長さ)/(直径)」ではダメ

Wikipediaを見ると「円周率とは、円の直径に対する円周の長さの比率のことをいい、数学定数のひとつである」と書かれてあります。

しかし、一部の細かいこと気にする人々（例えば解析学を専門にする数学者とか）は、この定義を受け入れません。この定義に対して、この手の人たちは反論します。
「円周の長さとは何か？定義されていないではないか！円周だけでなく、一般的な曲線の長さも定義するべきだ」
大学数学を知らない人には理不尽な質問に見えます。これに対して「曲線の長さは折れ線によって近似できます」とか答えると、今度は
「近似の仕方によって、異なった曲線の長さが得られる可能性がある。そのような可能性がないことを証明せよ」
と言われるでしょう。殴りたくなってくるかも知れませんが、この手の疑問は大抵の場合、この手の人たちによる自問自答で展開されるので殴らないでください。それと、これは真面目な議論です。実際、似たようなことを題材にした記事がno+e内に存在します。

上の記事では、不適切な近似を使っているのでよくないです。そして、Wikipediaに載っている「弧長」とか「ハウスドルフ測度」のように、曲線の長さを「適切な近似によって得られる値の中で最大のもの（雑に言ってます）」と定義すると、値が異なるとかの問題は起きません。

しかし、この定義だと別の問題が生じます。オイラーの等式$${e^{i\pi+1=0}}$$の証明など実質的な数学の議論が非常に難しい、あるいは実質的に不可能になります。定義が複雑すぎて扱いにくいのです（涙目）。

余談ですが最近、「コッホ曲線の長さは無限大」という話題について「証明はどうなっているのだろう？」と少し調べたのですが、「曲線の長さの話題には関わりたくないな」という感想に落ち着きました。この手の話題は、フラクタル曲線を専門に勉強する人向けの話だと思います。

最も無難な定義は？

以上の理由により、「曲線の長さ」という概念が使えないので、円周率の定義は別の方法で行う必要があります。円周率については様々な性質が知られているので、円周率を定義する方法も複数のあり得ます。

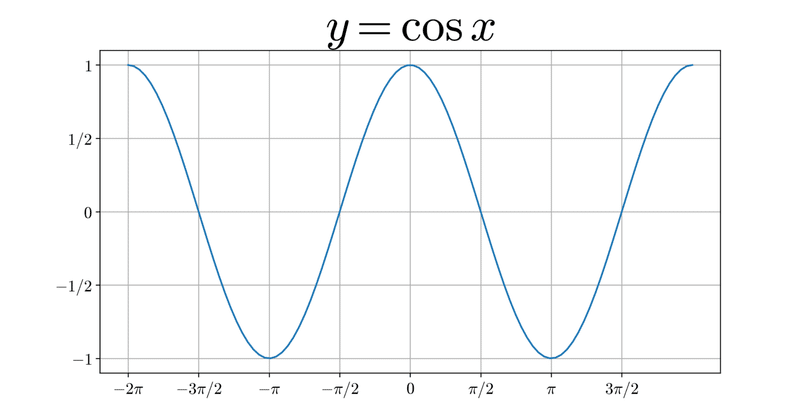
その中で、私が一番楽で使いやすい定義だと私が思っているのが、杉浦光夫『解析入門Ｉ』の定義方法です。すなわち、「$${\cos x = 0}$$を満たす最小の正の実数を$${\pi/2}$$と定める」という定義です。

確かに、回りくどいと笑えるような定義なのですが、曲線の長さに深入りすると精神を病みます。そのため、三角関数や正則関数のべき級数展開という、それほど難しくなく穏やかで平和で、それでいて飽きさせない世界の中で、円周率を定義するのが無難だと感じています。

あと、「円周率は半径長さが１の円の面積」という定義も自然ですが、前提としてルベーグ積分論を展開する必要があるので、回りくどさは控えめに言っても同じくらいです。

高校数学は「厳密ではない」

論争に巻き込まれたくないので括弧で括りましたが、大学の数学科で「実数の定義」とか「$${\varepsilon-\delta}$$論法」とかを勉強すると、高校で勉強した数学の議論が「厳密でない」と感じられるようになります。あくまで個人的な感覚の話と思ってください。物理学者とか、計算機科学の理論家とか、統計学関係者にケンカを売るつもりはありません。

数学者自身の厳密性の探求、つまり他人に質問すると殴られるが故の自問自答で展開される活動の一つに、小学校から高校までの数学の内容を（自分たちが納得できる形で）再構築するという活動があります。

ここに紹介した本では、第Ⅰ部４章までを使い、ZFC集合論から初めて実数の構成までを行っています。雑に流れを説明すると

1. 命題論理、述語論理の基礎の解説

2. ZFC公理系で集合を定義する

3. 自然数（の全体からなる集合）を定義

4. 自然数から整数（の全体からなる集合）を定義

5. 整数から有理数（の全体からなる集合）を定義

6. 有理数からコーシー列を使って実数（の全体からなる集合）を定義

といった感じです（実際は少し順番が前後します）。学生の時にこの本を自習した際は、ここまで読むのがかなり大変でした。しかし、実数の定義の完了は、微分積分の入り口に過ぎません。この本の議論の延長線上に、杉浦光夫『解析入門Ｉ』の議論を置くと、高校で勉強した微分積分の「厳密な」議論を学べます。

以上の経験があったので、私は『解析入門Ｉ』を「円周率の定義が書いてある本」と思っています。

上の記事に書かれている

という疑問については、「三角関数を図形で定義する高校数学の方が間違っている。べき級数や微分方程式を使って定義する方が自然である」というのがこの立場からの回答です。『解析入門Ｉ』の議論は、ある種の人たちにとっては、とても自然で違和感のない展開なのです。

最後に一つ付け足すと、Coqという証明支援システムでも、上で紹介したのと同じような議論を展開しています。実際、標準ライブラリで、円周率を定義している箇所を見ても

と書かれていて、プログラミング言語の詳細は分からなくても、$${\cos x =0}$$となる$${7/8\leq x \leq 7/4}$$を$${\pi/2}$$と定めているのが想像できます。