東京大学大学院 情報理工学系研究科の入試過去問の解答例です．この記事では2019（平成31）年度の数学（一般教育科目）第2問について解答・解説します．問題は研究科のWebサイトから見ることができます．

問題PDF

※この解答例は大学院・研究科に認められたものではありません．正確性についての保証は致しかねます．

(1)

解答

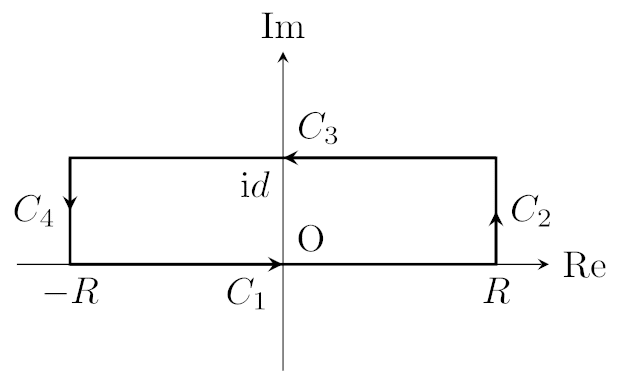
積分経路を図のように$${C=C_1+C_2+C_3+C_4}$$とする．ただし，$${R}$$は十分に大きな正の実数とする．$${f(z)=\exp(-az^2)}$$とおくと$${f(z)}$$は正則であるので，コーシーの積分定理より

$$
\oint_C f(z)\mathrm{d}z=0\tag{I}
$$

となる．なお，式(I)は$${d}$$の正負によらず成り立つ．ここで，

$$
\oint_C f(z)\mathrm{d}z=\int_{C_1}f(z)\mathrm{d}z+\int_{C_2}f(z)\mathrm{d}z+\int_{C_3}f(z)\mathrm{d}z+\int_{C_4}f(z)\mathrm{d}z\tag{II}
$$

であり，

$$
\begin{aligned}
\left|\int_{C_2}f(z)\mathrm{d}z\right|
&=\left|\int_0^d \exp\left(-a(R+iy)^2\right)\mathrm{d}y\right|\\
&\le\int_0^{|d|} \left|\exp\left(-a(R+iy)^2\right)\right|\mathrm{d}y\\
&=\int_0^{|d|}\left|\mathrm{e}^{-2iaRy}\right|\exp\left(-a(R^2-y^2)\right)\mathrm{d}y\\
&=\int_0^{|d|}\exp\left(-a(R^2-y^2)\right)\mathrm{d}y\\
&\le |d|\exp\left(-a(R^2-d^2)\right)\\
&\xrightarrow{R\to\infty}0,
\end{aligned}
$$

$$
\begin{aligned}
\left|\int_{C_4}f(z)\mathrm{d}z\right|
&=\left|\int_d^0 \exp\left(-a(-R+iy)^2\right)\mathrm{d}y\right|\\
&\le\int_0^{|d|} \left|\exp\left(-a(-R+iy)^2\right)\right|\mathrm{d}y\\
&=\int_0^{|d|}\left|\mathrm{e}^{2iaRy}\right|\exp\left(-a(R^2-y^2)\right)\mathrm{d}y\\
&=\int_0^{|d|}\exp\left(-a(R^2-y^2)\right)\mathrm{d}y\\
&\le |d|\exp\left(-a(R^2-d^2)\right)\\
&\xrightarrow{R\to\infty}0
\end{aligned}
$$

となるから，$${R\to\infty}$$のとき

$$
\int_{C_2}f(z)\mathrm{d}z=\int_{C_4}f(z)\mathrm{d}z=0
$$

となる．また，

$$
\int_{C_1}f(z)\mathrm{d}z=\int_{-R}^R\exp(-ax^2)\mathrm{d}x
$$

について，$${w=\sqrt{a}x}$$とおくと

$$
\begin{aligned}\int_{C_1}f(z)\mathrm{d}z&=\int_{-\sqrt{a}R}^{\sqrt{a}R}\exp(-w^2)\frac{1}{\sqrt{a}}\mathrm{d}w\\&\xrightarrow{R\to\infty}\frac{1}{\sqrt{a}}\int_{-\infty}^\infty\exp(-w^2)\mathrm{d}w\\&=\sqrt{\frac{\pi}{a}}\end{aligned}
$$

となる．さらに，

$$
\begin{aligned}\int_{C_3}f(z)\mathrm{d}z&=\int_R^{-R}\exp\left(-a(x+\mathrm{i}d)^2\right)\mathrm{d}x\\&\xrightarrow{R\to\infty}-\int_{-\infty}^\infty\exp\left(-a(x+\mathrm{i}d)^2\right)\mathrm{d}x\end{aligned}
$$

となるから，式(I),(II)より$${R\to\infty}$$のとき

$$
\begin{aligned}\int_{C_1}f(z)\mathrm{d}z+\int_{C_3}f(z)\mathrm{d}z&=0\\\sqrt{\frac{\pi}{a}}-\int_{-\infty}^\infty\exp\left(-a(x+\mathrm{i}d)^2\right)\mathrm{d}x&=0\end{aligned}
$$

$$
\int_{-\infty}^\infty\exp\left(-a(x+\mathrm{i}d)^2\right)\mathrm{d}x=\sqrt{\frac{\pi}{a}}\tag{答}
$$

となる．

解説

実軸に平行な積分経路でのガウス積分を求める問題です．コーシーの積分定理を利用すると，結果として実軸上での積分と変わらないということがわかります．

なお，$${s=\sqrt{a}(x+\mathrm{i}d)}$$と置換して与えられた公式を直接利用することはできません．なぜなら，その場合は

$$
\int_{-\infty}^\infty\exp\left(-a(x+\mathrm{i}d)^2\right)\mathrm{d}x=\frac{1}{\sqrt{a}}\int_{-\infty+\mathrm{i}d\sqrt{a}}^{\infty+\mathrm{i}d\sqrt{a}}\exp\left(-s^2\right)\mathrm{d}s
$$

となり，実軸上での積分にはならないからです．