
R|階層線形モデルで渋谷区の賃貸価格を予想する
以前の重回帰による賃貸価格の予測では、『最寄り駅ごとに賃貸価格の母集団分布(例えば各説明変数の母回帰係数)が異なりそう』という仮説を立て、1駅ずつ重回帰モデルを推定していきました。
ただ、駅が変わるとモデルの作り直しをしたりですんごいめんどくさい。
今回はそうした「最寄り駅」ごとに階層構造になっているデータに対する分析手法として知られている「階層線形モデル」を試してそうしたお悩みの解消を試みたいと思います( ˆoˆ )
■ 今回やりたいこと
・ 階層線形モデルを用いて賃料の予測をする(回帰問題に取り組む)
・ 予測の評価指数として各駅の決定係数 0.8 以上を目指す
■ 階層線形モデルとは
切片や傾きが各グループ(今回であれば各駅)ごとに正規分布に従って得られると仮定してモデルを推定します。
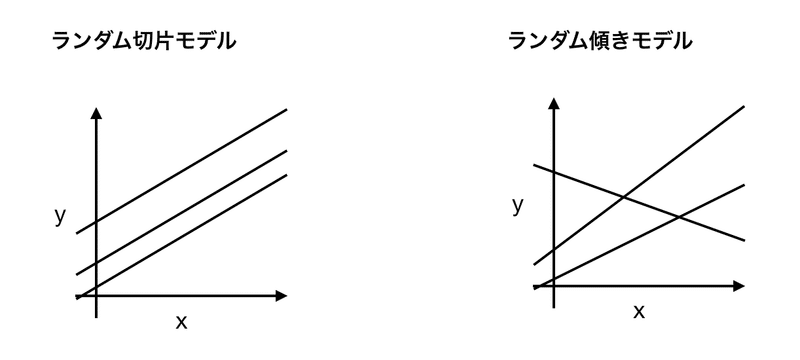
ランダム切片モデル
・ 各グループごとに切片が異なる(正規分布に従って得られるとする。)
・ 傾きは同じ
ランダム傾きモデル
・ 切片に加え、傾きもグループ間で異なる(正規分布に従って得られるとする。)
固定効果とランダム効果
・ それぞれの係数が従う正規分布の期待値を固定効果、期待値からの離れ具合(偏差)をランダム効果という。

階層線形モデルの嬉しいところ
・ 階層になっているようなデータを一括でモデルを作成することができ、解釈可能性も高くなる
・ サンプル数が少ない駅があっても推定ができる
■ lme4::lmer使い方
階層線形モデル作成のために lme4 パッケージ を使用します。
1. 基本
> library(lme4)
> model1 <- lmer(y ~ x1 + x2 + x3 + (1 + x1 | factor), data=data)
> model2 <- lmer(y ~ x1 + x2 + x3 + (0 + x1 | factor), data=data)・ 階層線形モデル式の x1 + x2 + x3 までは固定効果項、 (1 + x1 | factor) はランダム効果項
・ model1のようにランダム効果項の最初の値が 1 だと切片もランダム、model2のように 0 なら切片固定
2. ランダム効果変数が複数の場合
> model3 <- lmer(y ~ x1 + x2 + x3 + (1 + x2 + x3 | factor), data=data)・ factorに対するランダム効果変数を複数置きたい場合は (1 + x2 + x3 | factor) と書く
3. 回帰係数間の相関関係がないと仮定する場合
階層線形モデルでは、説明変数の回帰係数の間に相関関係を考えることが出来ます。例えば、敷地面積の回帰係数が大きければ駅徒歩の回帰係数の大きい傾向にあるなど。このような関係がないと仮定したいときは、以下のようにformulaを書きます。
> model4 <- lmer(y ~ x1 + x2 + x3 + (1 + x1 | factor), data=data)
> model5 <- lmer(y ~ x1 + x2 + x3 + (1 + x1 || factor), data=data)・ 回帰係数間の相関係数を 0 にするのであれば、model5のようにランダム効果項のバーを || と置く
■ データ観察
1. 駅の数と駅ごとのサンプルサイズを調べる
> rooms %>% group_by(station) %>% summarise(n())
# A tibble: 18 x 2
station `n()`
<chr> <int>
1 代々木上原駅 405
2 代々木八幡駅 369
3 代々木公園駅 353
4 代々木駅 304
5 代官山駅 219
6 初台駅 608
7 北参道駅 168
8 千駄ヶ谷駅 50
9 南新宿駅 56
10 原宿駅 96
11 参宮橋駅 248
12 国立競技場駅 4
13 幡ヶ谷駅 730
14 恵比寿駅 1118
15 明治神宮前駅 37
16 渋谷駅 651
17 神泉駅 156
18 笹塚駅 787国立競技場駅はサンプルサイズが4件とあまりにも小さく、適切なモデルの推定が出来ないと考えたため、今回は削除することにしました。
2. 駅ごとに面積と家賃の散布図を描いて、外れ値そうなのがないかチェック
> ggplot(rooms, aes(x=space, y=price)) + facet_wrap( ~ station) + geom_point() + stat_smooth(method = "lm", se = FALSE) + theme_gray(base_family="HiraKakuProN-W3")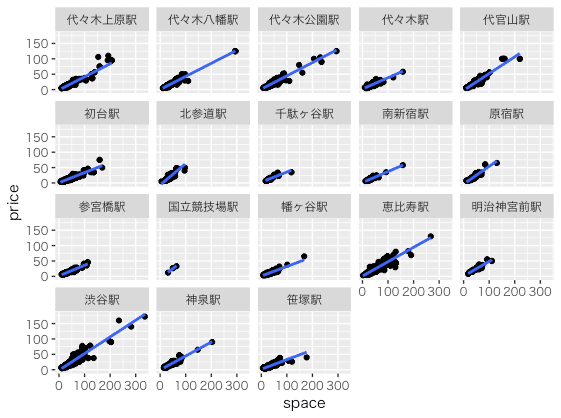
3. 極端な外れ値を除去
定期借家物件削除
・ 高すぎる(100万以上)物件
下宿やシェアハウス削除
・ 物件名〜荘という名前の物件
(共有部分が面積に含まれているような物件)
・ 専有面積が狭すぎる(10㎡より狭い)物件
国立競技場はサンプル数が少なすぎるため削除
4. 対数を取らない場合と対数を取った場合の散布図を確認
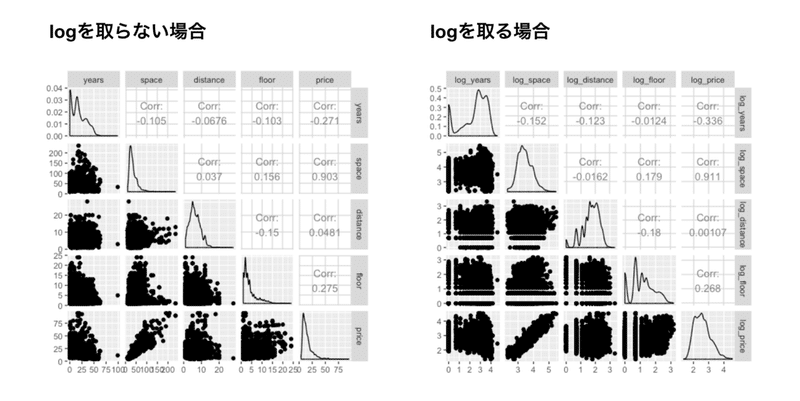
・ 対数を取ったほうが専有面積間で家賃の分散が同じようにみえる(階層線形モデルの等分散性のチェック)。
・ 説明変数・被説明変数の両方に関して対数を取り、推定に使用する
■ 階層線形モデルでモデル作成
実際の賃貸データを使ってモデルを作っていきます。
検証用にまずはデータを訓練データとテストデータに分割します。
1. データの分割
> library(tidymodels)
> splited_data <- initial_split(rooms, p = 0.75, strata = c('station'))
> training_data <- training(splited_data)
> test_data <- testing(splited_data)各駅ごとにテストデータが1/4の割合になるよう、層別サンプリング(stratified shuffle split)を行う。
2. lmer関数で階層線形モデルを推定
> model <- lmer(log_price ~ log_space + (1 + log_space || station), data=training_data)・ 先程散布図で確認したようにlog_priceとlog_spaceに高い相関があり、等分散性もみられたため、専有面積の対数をとった変数(log_space)を説明変数にする
・ 切片(家賃ベース)の高低と専有面積の大小からくる家賃の高低との間に相関関係はないと考えたため、回帰係数のランダム効果間の相関係数を 0 と置く
3. summary結果の確認
> summary(model)
Linear mixed model fit by REML ['lmerMod']
Formula: log_price ~ log_space + ((1 | station) + (0 + log_space | station))
Data: training_data
REML criterion at convergence: -3040.5
Scaled residuals:
Min 1Q Median 3Q Max
-3.8413 -0.6406 0.0344 0.6507 4.6524
Random effects:
Groups Name Variance Std.Dev.
station (Intercept) 0.059952 0.24485
station.1 log_space 0.008947 0.09459
Residual 0.029779 0.17257
Number of obs: 4725, groups: station, 17
Fixed effects:
Estimate Std. Error t value
(Intercept) -0.71476 0.06575 -10.87
log_space 0.95903 0.02425 39.55
Correlation of Fixed Effects:
(Intr)
log_space -0.137専有面積の固定効果(Fixed effects)の回帰係数が正の値になっているため、面積が広いほど価格が高そうというドメイン知識と合っていそうです。

↑で得た恵比寿の切片とlog_spaceの係数で回帰直線を確認します。
> plot(data_without_kokuritsu[data_without_kokuritsu$station == '恵比寿駅', c('log_space', 'log_price')])
> abline(-0.711884, 0.9951441)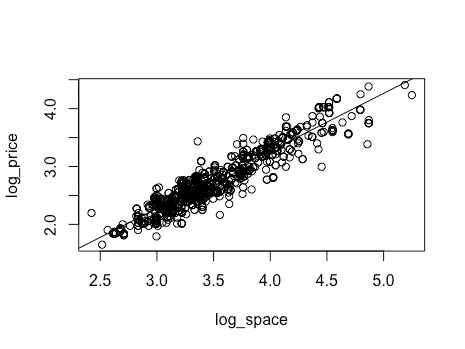
■ モデル評価
1. 決定係数の確認
各駅ごとに決定係数を確認したいと思います。
training: 推定時の決定係数(家賃の対数を外して計算)
test: 検証時の決定係数(家賃の対数を外して計算)
log_training: 推定時の決定係数(家賃の対数を取ったまま計算)
log_test: 検証時の決定係数(家賃の対数を取ったまま計算)
# A tibble: 18 x 8
station training test log_training log_test training_size test_size all_size
<chr> <dbl> <dbl> <dbl> <dbl> <int> <int> <int>
1 渋谷駅 0.825 0.842 0.883 0.902 484 161 645
2 千駄ヶ谷駅 0.823 0.775 0.914 0.855 34 15 49
3 代々木上原駅 0.925 0.915 0.932 0.910 299 103 402
4 原宿駅 0.784 0.956 0.845 0.902 67 29 96
5 明治神宮前駅 0.868 0.826 0.924 0.778 24 13 37
6 代官山駅 0.799 0.839 0.835 0.880 159 51 210
7 代々木駅 0.815 0.817 0.774 0.785 238 65 303
8 初台駅 0.834 0.802 0.842 0.845 462 139 601
9 笹塚駅 0.769 0.753 0.775 0.723 581 200 781
10 代々木公園駅 0.855 0.843 0.874 0.834 252 95 347
11 神泉駅 0.909 0.883 0.900 0.871 121 35 156
12 南新宿駅 0.918 0.790 0.849 0.771 44 12 56
13 代々木八幡駅 0.819 0.840 0.871 0.865 278 85 363
14 北参道駅 0.774 0.774 0.836 0.829 127 40 167
15 幡ヶ谷駅 0.807 0.838 0.796 0.833 538 186 724
16 恵比寿駅 0.844 0.813 0.870 0.860 836 278 1114
17 参宮橋駅 0.914 0.876 0.904 0.883 181 67 248
18 渋谷区全体 0.871 0.868 0.894 0.892 4725 1574 6303渋谷区全体の決定係数
・ 推定時・検証時ともに 0.8 後半でモデル自体の予測性能はかなりよさそう
各駅ごとの決定係数(training・test)
・ 概ね 0.8 以上
・ 各駅の推定時と検証時の決定係数に大きな変化がない
・ 南新宿駅の決定係数に差が見られるのはサンプル数が小さいせいで、テストのほうが訓練より決定係数が悪い現象は過剰適合※を示唆しているものとは言えないと考える
※ 過剰適合(過学習・オーバーフィッティング):モデルが複雑すぎるために訓練データに過剰に当てはまり、未知のデータに対して予測精度が低くなる状態のこと
2. 残差プロットの確認
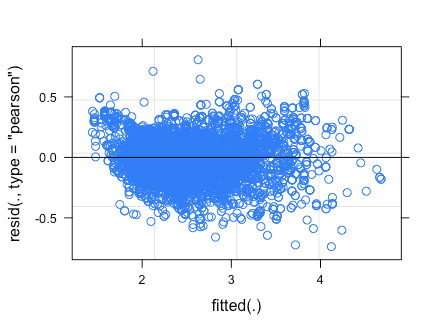
上下のばらつきも偏りがなく、0 を中心としてまとまっているのでよさそう。
3. Q-Qプロットの確認
HLMdiagパッケージで物件レベルのQ-Qプロットを確認します。
> library(HLMdiag)
> resid1 <- HLMresid(model, level = 1, type = 'LS', standardize = TRUE)
> ggplot_qqnorm(x = na.omit(resid1$LS.resid), line = 'rlm')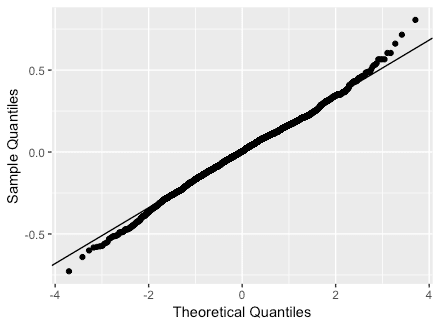
若干右上が外れていますが概ねよさそうです。
以上から今回のモデルは妥当だと言えそうです。
■ モデルの考察
・ 切片の固定効果と比較してランダム効果がやや大きいので各駅ごとに家賃のベースが異なるかもしれない
・ 専有面積の固定効果と比較してランダム効果は小さいので各駅ごとに面積の増加に対して家賃がどれだけ高くなるかはさほど大きく違わないかもしれない
・ → ひょっとするとランダム切片モデルでもよかった可能性がある
渋谷区全体
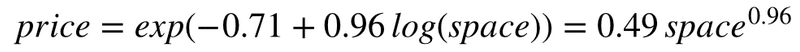
渋谷区全体では、0.96乗を1乗として見たときに、面積が1㎡広くなると賃料は4,900円増加するようです。
※ spaceの指数: 面積の価格に対する弾力性という
各駅ごと
(Intercept), log_space: ランダム効果
space_elasticity: 弾力性
increase: 弾力性を1とみなしたとき、面積1㎡あたりに増加する賃料(万)
(Intercept) log_space space_elasticity
代々木上原駅 -5.246001e-02 -0.003368677 0.9556636
代々木八幡駅 -9.618074e-02 0.028776319 0.9878086
代々木公園駅 -3.121204e-02 0.035172277 0.9942046
代々木駅 1.579823e-01 -0.042189230 0.9168431
代官山駅 -5.421307e-02 0.051477602 1.0105099
初台駅 1.395273e-01 -0.093421536 0.8656108
北参道駅 -6.300289e-01 0.215660779 1.1746931
千駄ヶ谷駅 -4.795593e-02 0.002003871 0.9610362
南新宿駅 9.810516e-02 -0.046588307 0.9124440
原宿駅 -1.255493e-01 0.065729577 1.0247619
参宮橋駅 2.393348e-01 -0.089726112 0.8693062
幡ヶ谷駅 2.133135e-01 -0.127262193 0.8317701
恵比寿駅 2.875997e-03 0.036114078 0.9951464
明治神宮前駅 1.183978e-05 0.035050543 0.9940828
渋谷駅 -1.756146e-01 0.080525533 1.0395578
神泉駅 -5.514785e-02 0.021029193 0.9800615
笹塚駅 4.172115e-01 -0.168983715 0.7900486各駅の弾力性を地図にプロットしてみましょう。
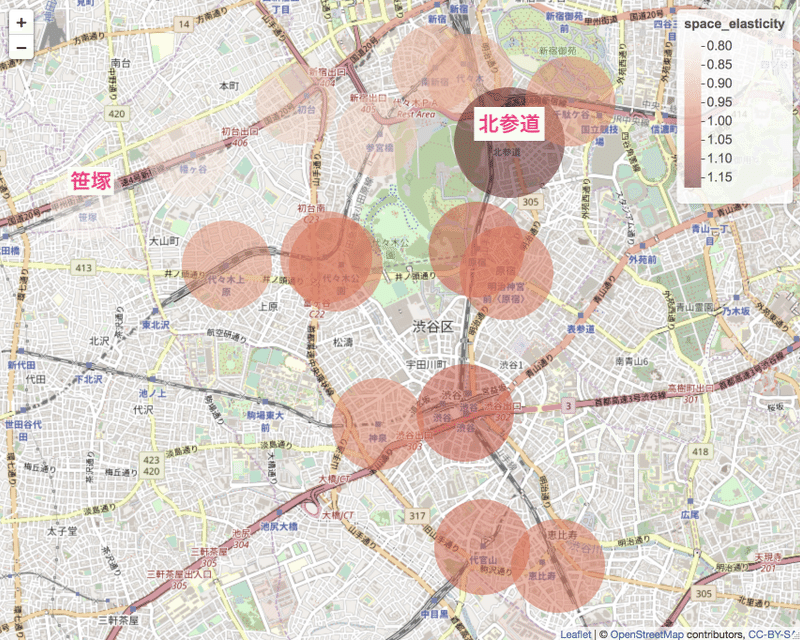
笹塚の弾力性が低く、北参道の弾力性が高いですね。
北参道駅と笹塚駅が対象的なのでプロットして比較してみたいと思います。
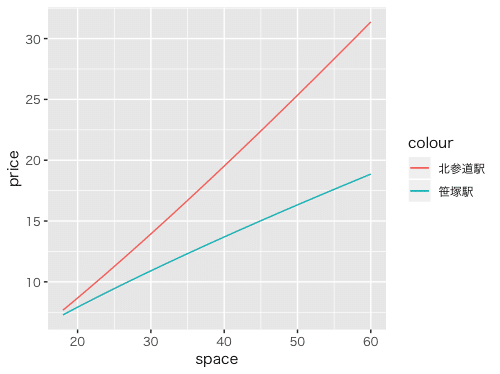
北参道は弾力性が高いので専有面積が広くなるにつれ笹塚の賃料と差が開いていく傾向にある。安く広い賃貸に住みたいなら笹塚がよさそうです。
※ 北参道駅が最寄りの賃貸は最低18㎡〜だったのでx軸の値は18から描画しています。
■ まとめ・今後やりたいこと
1つのモデルで渋谷区全体の賃貸を予測・説明することができるようになったので、上で触れたように駅ごとにどのような賃料の傾向があるのかもわかりやすくなってどの地域に住みたいか判断材料にもなりそうですね!
今回専有面積のみ説明変数に使用したので、次は他の変数を足すなどして決定係数が 0.9 以上になるような精度の高いモデルが作れそうかモデル比較をしてみたい...!
この記事が少しでも階層線形モデルをRでやってみたいな、という方の役に立ったらうれしいです 😌
■ 参考資料
・ Rによる多変量解析入門 データ分析の実践と理論
・ Fitting Linear Mixed-Effects Models Using lme4
・ HLMdiag: A Suite of Diagnostics for Hierarchical Linear Models in R
Special Thanks
utaka233:弊社で統計を教えてくれてる先生。今回もめっちゃ色々アドバイスいただいた、とってもありがたい存在(拝んどく) 🙏🙏
kawaida_:可愛い見出し画像をさらさら〜っと作ってくれたスーパーデザイナーさん。おどろいた。尊敬しかない。
統計の本、もしくはわんこにおいしいお菓子を買うのに使わせていただきます( *ˆoˆ* )
