移動平均線はテクニカル分析において最もシンプルで、わかりやすく初心者から上級者まで幅広く利用されるトレンド分析です。

その移動平均について少し視点を変えて考察します。

前回の投稿でヒストリカルボラティリティを用いてボリンジャーバンドを作成してみました。その際、ボリンジャーバンドの基準線を移動平均線ではなく片対数の回帰直線を用いるということを行いました。移動平均はその特徴として遅行性が挙げられます。片対数の回帰直線を用いるとその遅行が抑えられるという利点があります。ここではテクニカル分析における基本である移動平均線とその改善となりうる片対数回帰直線について深堀してみたいと思います。

片対数回帰直線

まずは『片対数回帰直線』について簡単に解説します。片対数回帰直線というはX軸、Y軸でグラフ化した際にそのいずれかを対数にして回帰直線を引くというものです。

前回、ヒストリカルボラティリティ(HV)を用いたボリンジャーバンドということでHVボリバンというものを提案しました。HVボリバンは「ボリンジャーバンドを、対数値の線形回帰によるミッドバンドと、対数正規分布による標準偏差に置き換えることで、BSモデルに基づいたものにしよう」というアイデアです。今回の『片対数回帰直線』というのはHVボリバンにおける『対数値の線形回帰』の部分を意味しております。

片対数としているのは、株価$${S}$$を対数変換した$${\ln(S)}$$に対して回帰直線を引くためです。なぜ対数変換するかというのは、ブラック・ショールズモデルの式において株価$${S}$$を対数変換した$${\ln(S)}$$が直線の式になるからでした。この直線の傾きは μ で表現され株価のトレンドを表しています。この回帰直線を引くことで１日先の基準値を設定するということを行っておりました。

詳細な説明は下記記事にありますのでご参照ください（無料記事部分でご覧いただけます）

移動平均線

ここで取り上げる移動平均線は単純平均移動線(SMA)になります。

移動平均線はテクニカル分析において最も広く使用されるものかもしれません。移動平均は一定期間の価格を平均化することで不規則な上下変動を排除してデータを平滑化するというものです。使い方としては、移動平均線に対して現在の価格がどこにあるかを比較するといったものが多いかと思います。
https://www.jibunbank.co.jp/products/foreign_deposit/chart/help/sma/
https://www.fxbroadnet.com/tech/technicalchart/tech01.jsp

移動平均線の特徴としてよく挙げ上げられるのは、計算対象の期間が長くなるほど変動が緩やかになるが、価格変動に対しての反応は鈍くなる遅行指標であるという点です。単純平均だと平均期間が長いほど過去のデータに引っ張られやすくなります。短期線だと鋭敏性が高いが、ダマシが多く信頼性が低くなる傾向があり、長期線だと鋭敏性が低くなるが、ダマシが少なく信頼性は高くなります。そのため複数の移動平均線を組み合わせて使用されることが多いです。

移動平均線に対して現在の価格がどこにあるかを比較するような使い方は、縦軸を価格S、横軸を時間tとしたグラフにおいて縦方向の比較を見ていることになります。一方で、制御的な考え方をすると横方向の比較で見ることもできます。これは元データに対して移動平均がどのくらい遅れるか、という見方になります。

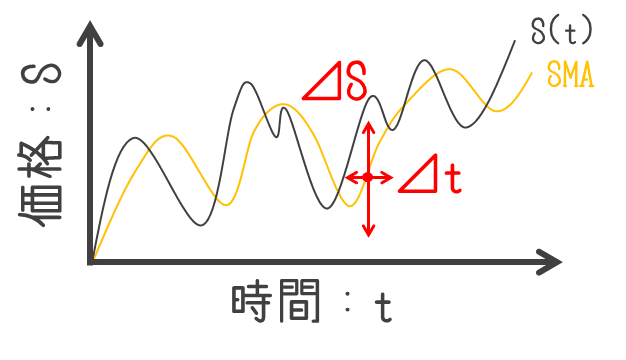
移動平均を縦方向にみる、横方向にみる、という考え方は下記の記事が参考になります。

価格変動が理想的な単一周期の正弦波であったとき、移動平均線の遅れは計算対象期間のおおよそ半分の日数になります。例えば、10日平均だと5日遅れ、200日平均だと100日遅れという具合です。

ただし、例外として計算対象期間が変動周期の整数倍である場合、移動平均線は常に一定値となって移動平均線に変動が生じなくなることから遅れの概念がなくなります。これによって変動周期が短い急な変動成分がカットされることから、移動平均はハイカットフィルタ、ローパスフィルタとして扱われたりします。

では、本当に移動平均線の遅れが計算対象期間のおおよそ半分になるのか試しに計算してみましょう。

任意の関数はフーリエ級数、つまりsinとcosの和で表せられますので、T日移動平均線と比較するということは大雑把にみると『T/2日前の株価変動から急激な変動を取り除いたものと比較している』ことを意味します。

それでは、片対数回帰直線の場合はどのくらいの遅れになるのでしょうか？

基本波形における考察

片対数回帰直線の遅れ時間は計算が難しいためここでは実際にグラフ化してどのくらい遅れがあるか見てみたいと思います。ここでは、基本波形を参考にして正弦波、矩形波、三角波、のこぎり波について見てみます。簡易化のため、各波形は2を中央値として±1の変動範囲を持つものとし、計算期間は20日、回帰直線は最小二乗法による算出とします。

まずは正弦波について。変動周期が10日、20日、40日、80日のケースでそれぞれ以下のようになります。

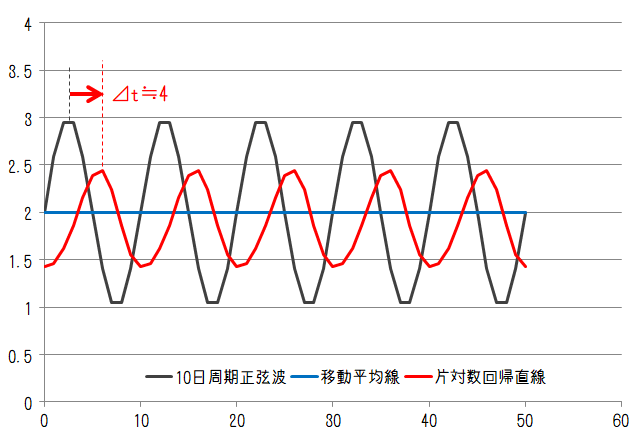
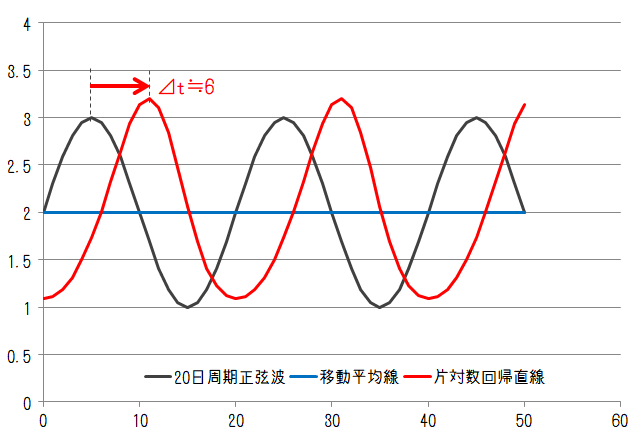
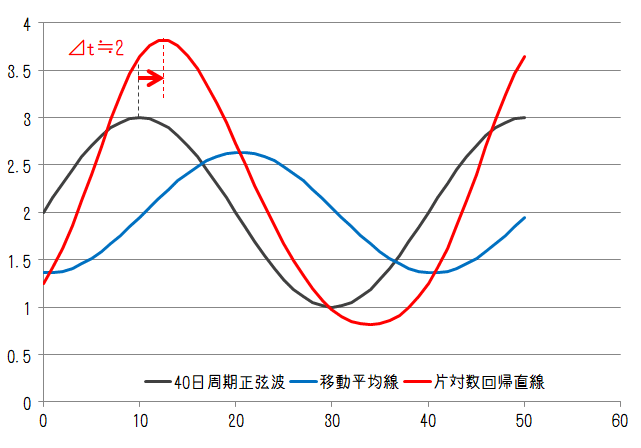
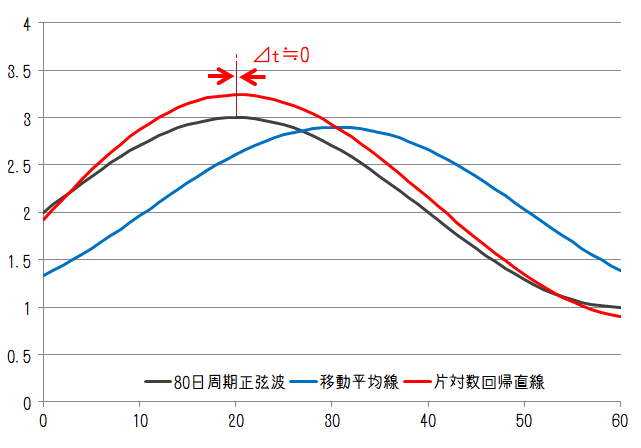
計算期間20日は10日周期、20日周期に対してそれぞれ2倍、1倍の長さであることから、10日周期、20日周期の移動平均線は常に2になります。一方、片対数回帰直線はいずれの周期においても変動を持っています。

20~80日周期の移動平均線と比較すると片対数回帰直線のピーク値は元波形のピーク値に対して乖離が大きくなっています。移動平均線は過去の平均値であるためピーク値を超えることはありません。片対数回帰直線は過去の流れ（トレンド）が反映されるためオーバーシュート気味になっています。

片対数回帰直線のピーク位置は移動平均線のピーク位置よりも元の波形に近い位置にあることから、片対数回帰直線の遅れ時間は移動平均線に比べて小さいことがわかります。移動平均線のピークの遅れが20日の半分、つまり10日であるのに対して、片対数回帰直線は各変動周期でおおよそ4日、6日、2日、0日の遅れとなりました（ここで「おおよそ」としているのは実際のピークは分割数の関係で見えなくなっているためです）この結果は変動周期によって遅れの量が異なることを意味していると言えます。

次に矩形波について。矩形波は2レベルの間を規則的かつ瞬間的に変化する変動になります。変動周期が20日、40日のケースでそれぞれ以下のようになります。

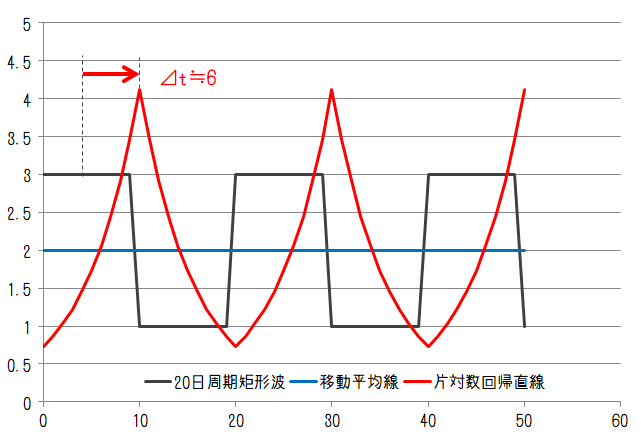
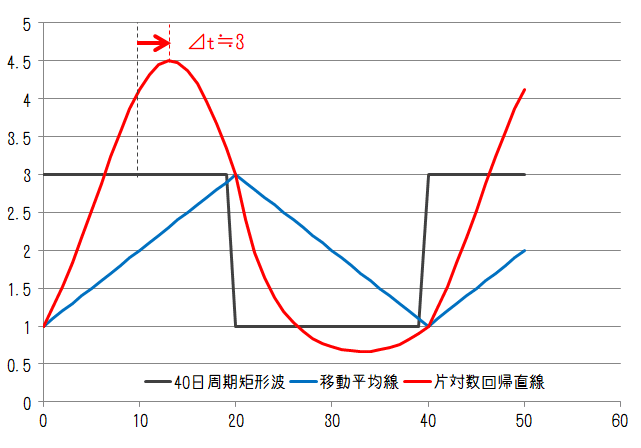
ここでも20日周期の移動平均線は常に2、40日周期のピーク位置は矩形波のピーク中央位置から10日となっています。40日周期の片対数回帰直線のピーク位置は移動平均線のピーク位置よりも左側にあるため、ここでも片対数回帰直線のほうが遅れ時間が小さくことがわかります。また、移動平均線に比較するとピーク値の乖離は大きくなっています。遅れは各変動周期に対しておおよそ6日、3日となりました。

続いて三角波について。三角波は正弦波に似ていますが線形的に変化する変動になります。変動周期が20日、40日のケースでそれぞれ以下のようになります。

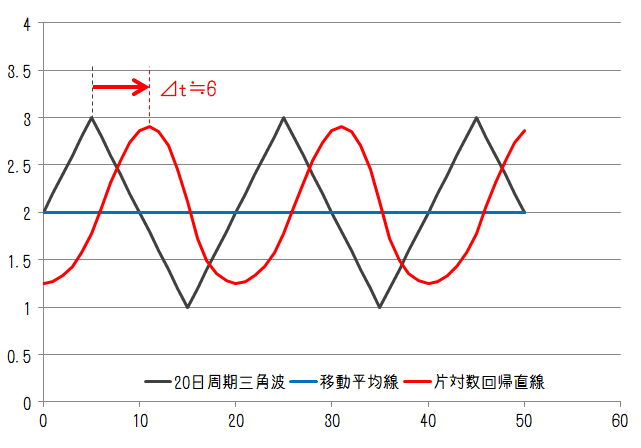
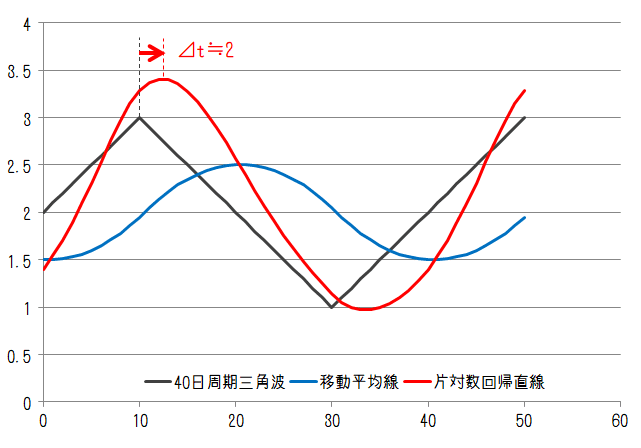
移動平均線と片対数回帰直線の関係はここでも矩形波と同じになります。遅れは各変動周期に対しておおよそ6日、2日となりました。

最後にのこぎり波について。のこぎり波は徐々に増加したのち急降下するということを繰り返す、もしくは逆に徐々に下がっていって急上昇することを繰り返す変動パターンです。変動周期が20日、40日で徐々に上昇するケース、徐々に下降するケースでそれぞれ以下のようになります。

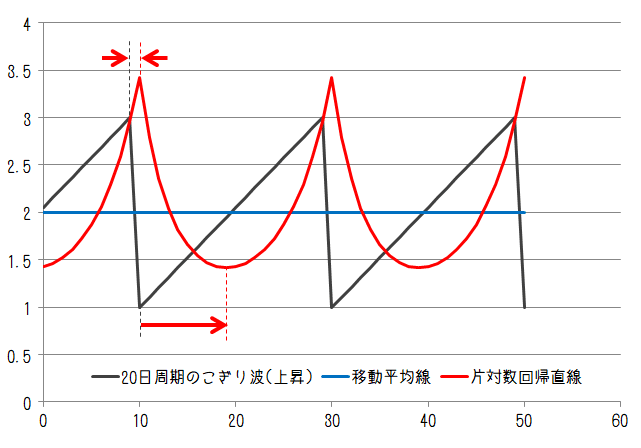
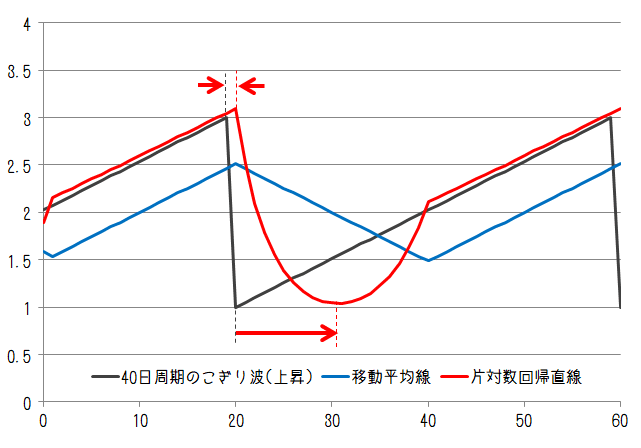
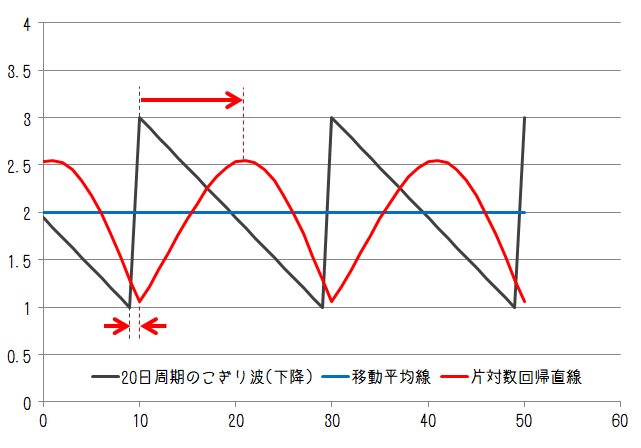
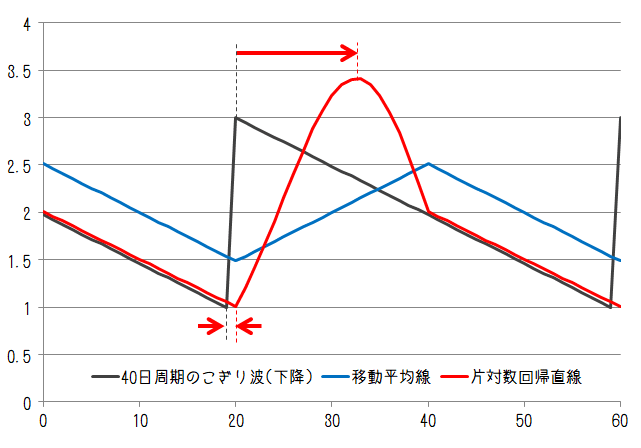
ここでの片対数回帰直線は急激な変動前のピーク位置はほぼ元の変動ピーク位置と一致していますが、急激な変動後のピーク位置は大きく遅れています。それでも40日周期においては移動平均線よりも遅れは小さくなっています。

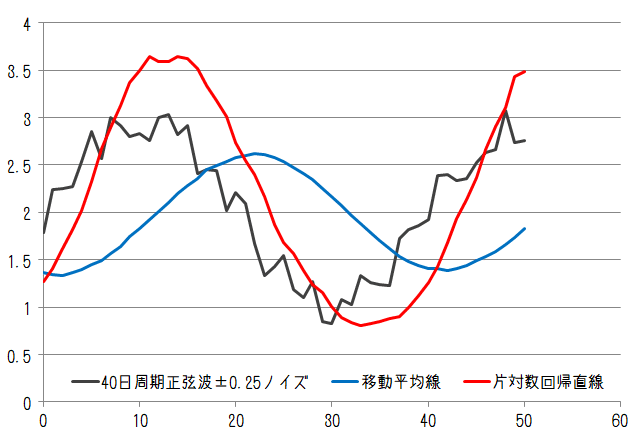
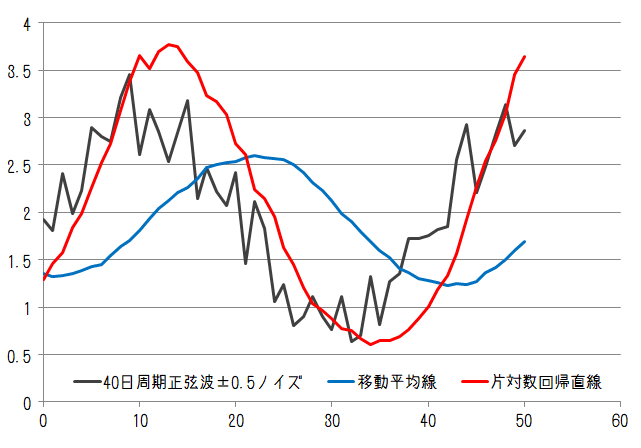
40日周期の正弦波に±0.25と±0.5のランダムノイズを乗せた場合でもピーク位置は概ね識別できています。これらのことから『片対数回帰直線は移動平均線よりも価格のピーク値の乖離は大きくなるが時間方向の遅れを小さくすることができる』と言えそうです。

まとめ

今回は移動平均線と片対数回帰直線の深堀をしてみました。どうやら移動平均線に対して片対数回帰直線を用いることで遅れ時間を小さくできる見込みがあることがわかりました。計算期間が同じ20日だとしても20日移動平均線だと遅れ時間が約10日なのに対して、片対数回帰直線の遅れ時間はその1/3~1/2程度になります。

これを応用するとさらに面白い指標ができそうです。

移動平均線と片対数回帰直線を組み合わせると、移動平均線を片対数回帰直線が下から上、もしくは上から下に交差するような動きが生まれます。これは同じ期間を元にしたトレンド線同士でゴールデンクロス・デットクロスの概念を取り入れられることを意味します。このゴールデンクロス・デットクロスへの発展については別途記事にまとめたいと思っております。

HVボリバン→片対数回帰直線と展開してきたので、次回の投稿ではHVボリバンのバンド幅設定について深堀してみます。次回の投稿もご覧いただけると幸いです。ではでは🎩

（この記事は投げ銭制で全文無料公開しています。気に入っていただけた方は投げ銭いただけますと励みになります。）