大学生のときの基礎実験の時間中、実験をさぼって電卓で遊んでいたら、以下の事実を発見しました（「実験、さぼるなよ！」というツッコミが来そうです。すみません…）。

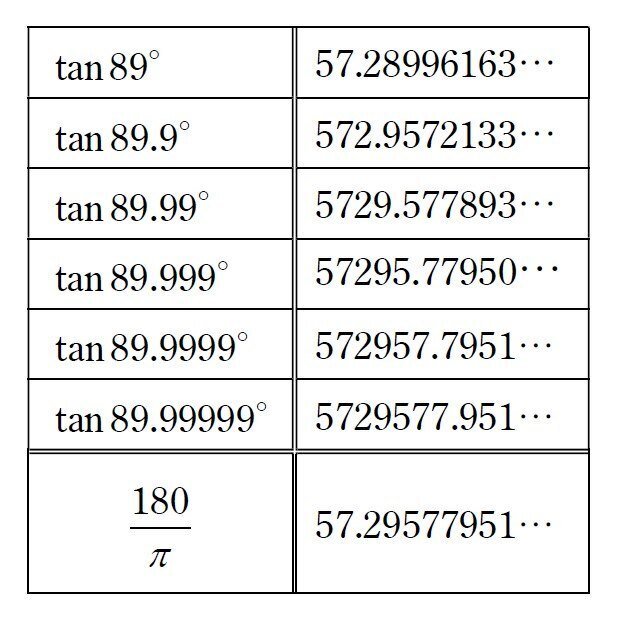
何と、$${89.99\cdots9^{\circ}}$$の末尾に$${9}$$を1つ追加すると、$${\tan}$$の値が約10倍になるのです！しかも、はじめの$${\tan 89^{\circ}}$$の値は$${\displaystyle \frac{180}{\pi}}$$の値とほぼ一致しています。ちょっと感動しませんか！？

興味を持った方は、これが成り立つ理由をぜひ考えてみてくださいね。
以下、理由を簡潔に説明します。

$${89.99\cdots9^{\circ}}$$（小数第$${1}$$位から第$${n}$$位までがすべて$${9}$$）は$${\displaystyle 90^{\circ}-\frac{1^{\circ}}{10^n}}$$に一致します（$${n=0}$$のときは$${\displaystyle 89^{\circ}=90^{\circ}-\frac{1^{\circ}}{10^0}}$$を表すとする）。これを弧度法で表すと、$${\displaystyle \frac{\pi}{180}\left(90-\frac{1}{10^n}\right)=\frac{\pi}{2}-\frac{\pi}{180}\cdot\frac{1}{10^n}}$$です。これの$${\tan}$$は、$${\displaystyle \left(\tan\frac{\pi}{180}\cdot\frac{1}{10^n}\right)^{-1}}$$です（$${\displaystyle \tan\left(\frac{\pi}{2}-\theta\right)=\frac{1}{\tan\theta}}$$に注意）。
ここで、$${\displaystyle \frac{\pi}{180}\cdot\frac{1}{10^n}}$$は$${0}$$に近いので、近似式
　　　　　「$${\theta \approx 0}$$のとき$${\tan\theta \approx \theta }$$」
を用いることで
　　$${\displaystyle \left(\tan\frac{\pi}{180}\cdot\frac{1}{10^n}\right)^{-1}\approx \left(\frac{\pi}{180}\cdot\frac{1}{10^n}\right)^{-1}=\frac{180}{\pi}\cdot10^n}$$
が得られます。これは、初項$${\displaystyle \frac{180}{\pi}}$$、公比$${10}$$の等比数列の第$${n}$$項です。//