はじめに

初めての投稿です。
気になっていることを中心に取り留めもなく書いていこうと思います。

今回のテーマ

複数の点の座標をもとに、最もうまく近似される直線を推定するということを考えています。
これまでは他の方の考察ページなんかを覗きながら計算していましたが、リンクが消えてしまったりで、欲しい情報を得るのに時間がかかるようになったので、ここらで自分の考えをまとめておこうかと思った次第です。

まずは二次元平面上で考える

手始めに二次元平面で直線フィッティングを考えます。(この辺は高校数学の範囲かな。)
ここで考えるのは、２次元平面(x-y座標系)に分布している複数の点の間を通って、すべての点の傾向を最もよく表す直線方程式を求める方法です。

こんな感じの10個の点が分布している時、散布図を書くと次のようになります。

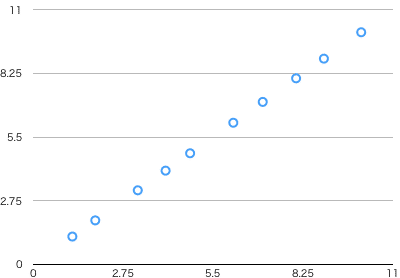
この散布図を人間が見ると、「あー、だいたい直線的に並んでるなー」と思うわけですが、この10個のデータをより精度よく利用しようとすると、より正確に分布の傾向を求める必要が出てきます。

この「傾向」ですが、今回のデータの場合、"直線方程式"として表現します。(または一次方程式)
（蛇足：改めて考えると、ここで直線だ!と判断するのは人間の感覚なんですよね。(または慣例、経験則) 二次以上の高次方程式として表現するっていう判断は人間が関わらない時はどうやってやるんだろ?）

直線方程式を最小二乗法で求める

直線方程式を求める方法はいくつかありますが、最小二乗法を使っていきます。(仮に求めた直線と、元のデータとのズレ量を計算していって、一番ズレ量が小さい直線が、最もよく近似された直線だと判断する方法ですね。)

それぞれの点と直線とのズレ量は、点と直線の距離として捉えられ、公式を使って求められます。

点(x0,y0)と直線ax+by+c=0の距離(=点から直線に垂直に下ろした線の長さ)dは、次の式で表される。

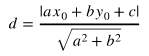
ただ、これをこのまま使っちゃうと計算がひどく面倒になるので、少し楽をしてみます。
点と直線のズレをyの値だけのズレと考えると、式が次のように簡単になります。

このdの総計を今回の10点分で考えますが、この総計を取る時の方法として以下の方法があります。

SAD(Sum of Absolute Difference)：対象とするdの絶対値|d|の総和を取る
SSD(Sum of Squared Difference)：対象とするdの二乗和(d*dの総和)を取る

今回はSSDを採用します。

いよいよ直線方程式を求めていきます。
10点分のdのSSDは次のように表されます。(iを添字として1から10まで合計する)
※ここで、誤差はεを用いて表される場合が多いので、これを使って表現しています。

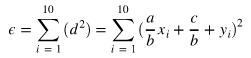
このεに対し微分を考えていきます。
ここで求めたいのはεが最小となる係数a,b,cの組み合わせなので、εをa,b,cそれぞれで微分し、その値が0となる(=極小)場合を考えてみます。
(本来微分値が0であることは極大であることも含みますが、今回のケースでは極大は存在しないので、極小とイコールとして考えています。)

※思ったより長くなってしまったので、ここで分割します。
次回、続きを書いていきます。