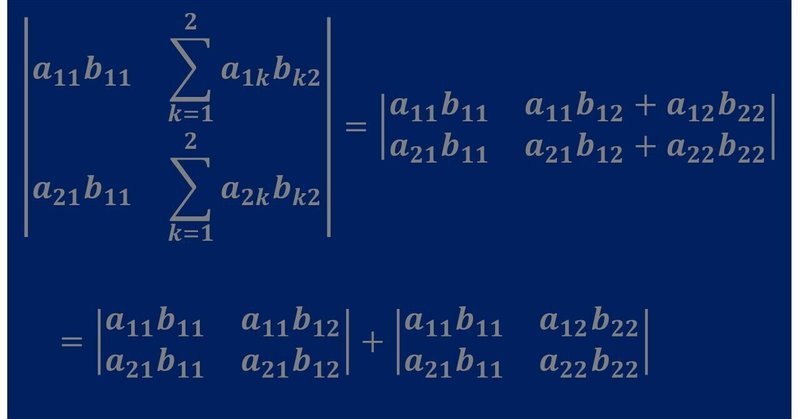
行列式の多重線形性をn次正方行列で
行列式の多重線形性について2次正方行列で使って練習する内容になります。
行列式の多重線形性で、行列式のある列が和の形になっているときに、2つの行列の和に書き換えることと、ある列が一斉にc倍されているときに、その行列式全体をc倍したものに書き換えるということをやってみます。
この2つを合わせて、線形性といいます。3次以上の行列式について、どの列についても線形性が成り立つので、多重線形性といいます。行列式の一般論を理解しつつ、具体例で様子を押さえておくと、理論の深い理解につながるかと思います。
行列式の多重線形性

j列が一斉に線形和となっているときに、右辺の形と等しくなります。この証明は、行列式の定義に分配法則を使えば、すぐに得られます。シグマ計算は、行数を対称群で置換してできる項の和をとる定義で計算します。

これで証明が完了です。スカラー倍のcがシグマΣの外に出せました。つまり、c倍した行列式どおしの和になるわけです。これは、j列が2個の項の線形和になっているときですが、3個以上の線形和のときにも、「1個 + 残り」という形にして行列式を分けていけば、同様にして証明できます。
また、j行が一斉に線形和となっているときにも、列数を対称群で置換する定義で計算すると、同じように分配法則から証明ができます。
行列式の多重線形性を使う練習
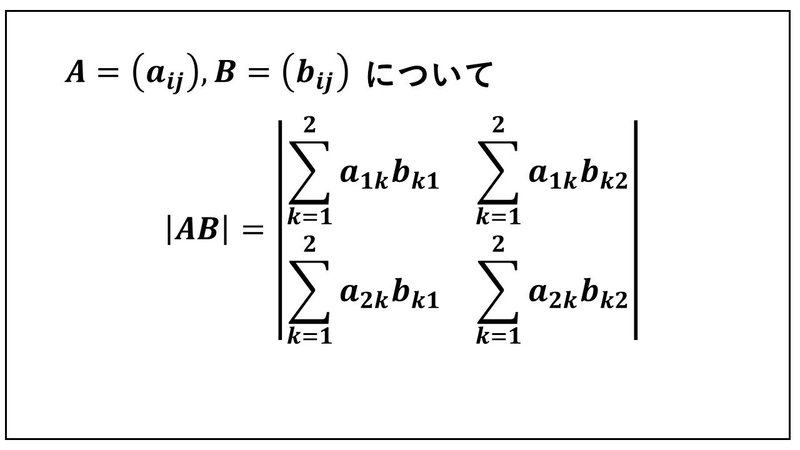
複素数を成分とする2次正方行列AとBについて、積ABの行列式|AB|を多重線形性を使って計算します。まず、行列の積の定義に基づいて、各成分をシグマを使って計算し、|AB|を考えます。
|AB|の1列目を見ると、(1, 1)成分と(1, 2)成分に和の形が現れています。

ここで、行列式の多重線形性の和についての変形をします。

2つの行列式の和に書き換えることができます。この右辺の2つの項である行列式の2列目を見ると、まだ和の形があります。それぞれの行列式について、再び多重線形性の和の変形をします。
まず、左の項から変形します。その後で、右の項の変形をします。合計で(2 × 2)個の項で|AB|を表すことになります。

このように、先ほどの左の項の行列式から2個の項が出てきました。残っている右の項の行列式も多重線形性の和の変形をして、2個の行列式の和に書き換えます。
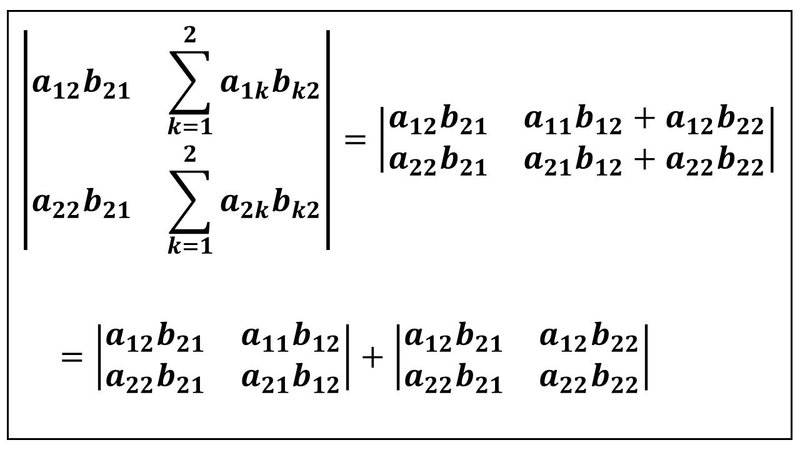
これで、先ほどの左の項の書き換えと合わせて、|AB|が4個の行列式の和で表されることになります。ここまでのまとめとなる次の図をご覧ください。

このように、2次正方行列の場合は、多重線形性の和の変形で、4個の行列式の和に書き換えることができます。3次の正方行列の場合は、同様のやり方で、(3 × 3 × 3)個の行列式の和へと変形されます。一般に、n次正方行列の場合は、「nのn乗」個の行列式の和に変形できます。
次に、多重線形性である列が一斉にc倍されているときは、行列式全体をc倍に等しくなる書き換えをします。ここまで1つの行列をシンプルにすると、0になる行列式が出てきます。行列式の性質で、同じ列が2個以上あるときは、行列式の値が0になります。
実は、0になる行列式を省くと、2!個の行列式だけが残ることになります。一般に、n次の正方行列の場合は、n!個の行列式が残ることになります。
まずはじめの2個の行列式を多重線形性で変形し、その後、残りの2個の行列式を変形します。

この変形をすると、1列と2列が同じになっている行列式が出てきたので、その行列式の値が0であることから、省いて良いことになります。
この調子で、残りの2個の行列式も多重線形性で変形します。

また0になる行列式が見つかったので、それは省きます。そして、先ほどの変形したものと合わせると、|AB|が、残った2つの項の和で表されます。これが赤枠の式になります。
はじめの|AB|は、シグマ記号のある複雑な行列式でしたが、多重線形性を利用すると、このようなシンプルな形にまで変形できました。このnote記事では、途中の計算過程を書いて説明してきましたが、多重線形性の理解が進むと、ここまでスムーズに書き換えられるようになります。
もう少し行列式の性質を使うと、赤枠の等式を、さらに|AB| = |A||B|に変形することができます。

行列Aの1列目と2列目を入れ替えた行列式について、行列式の交代性を使います。そうすると、プラスマイナスが逆転します。|A|は1つの複素数なので、分配法則でくくり出すと、括弧の式は行列Bの行列式です。これで、|AB| = |A||B| となります。
ここから、行列式の多重線形性と交代性を導き出そうと思います。
行列式の多重線形性と交代性
複素数を成分とするn次正方行列Aがあったとき、a[i]をAのi行目の成分で作った行ベクトルとします(i = 1, ・・・, n)。これらn個の1行n列の行ベクトルをn個の変数として、Aの行列式の値を対応させることを考えます。
Aの成分は複素数なので、行列式|A|は複素数となっています。
det(a[1], a[2], ・・・, a[n]) = |A| とn個の行ベクトルの組に対して、|A|という複素数を対応させる関数detについて、次のような線形性が成立します。
b[1], ・・・, b[n]とc[i](iは1からnまでのどれかの自然数)を複素数を成分とする行ベクトルとし、pとqを複素数とします。
det(b[1], ・・・,pb[i] + qc[i], ・・・, b[n])は、
p×det(b[1], ・・・, b[i], ・・・, b[n])と
q×det(b[1], ・・・, c[i], ・・・, b[n])の和となります。
これは、i番目について2つの行ベクトルの一次結合についての線形性ですが、2つで成立すると、3つ以上の有限個の行ベクトルの一次結合についても帰納法で導けます。
pb[i] + qc[i] + rd[i] は、加法についての結合法則から、
pb[i] + (qc[i] + rd[i]) と考え、2個の行ベクトルの一次結合に線形性を使うという操作を有限回繰り返すことで、有限個の一次結合について、線形性が成り立ちます。
また、どの行についても線形性が成り立つので、多重線形性といいます。
さらに、次の交代性も成立します。
iとkを1以上n以下の自然数でi < kとすると、
det(b[1], ・・・, b[i], ・・・,b[k], ・・・, b[n])
= -det(b[1], ・・・, b[k], ・・・,b[i], ・・・, b[n]) となります。
i番目のk番目の行ベクトルをひっくり返すと、行列式の値のプラスマイナスが反対になります。このことから、次のことが分かります。
i < kで、b[i]とb[k]が等しい行ベクトルだとすると、
-det(b[1], ・・・, b[k], ・・・,b[i], ・・・, b[n])
= -det(b[1], ・・・, b[i], ・・・,b[k], ・・・, b[n]) なので、
2det(b[1], ・・・, b[i], ・・・,b[k], ・・・, b[n]) が0と等しくなり、
det(b[1], ・・・, b[i], ・・・,b[k], ・・・, b[n]) = 0 となります。
以上のn個の行ベクトルに複素数値を対応させる写像(関数)であるdetを使って、表紙に書いているブロック対角行列の行列式が、確かに対角上のブロック行列の行列式の積となっていることを確かめます。
ちなみに、(x)という1行1列の正方行列が1つ目の対角上のブロック行列で、行列式|(x)|はxとなります。
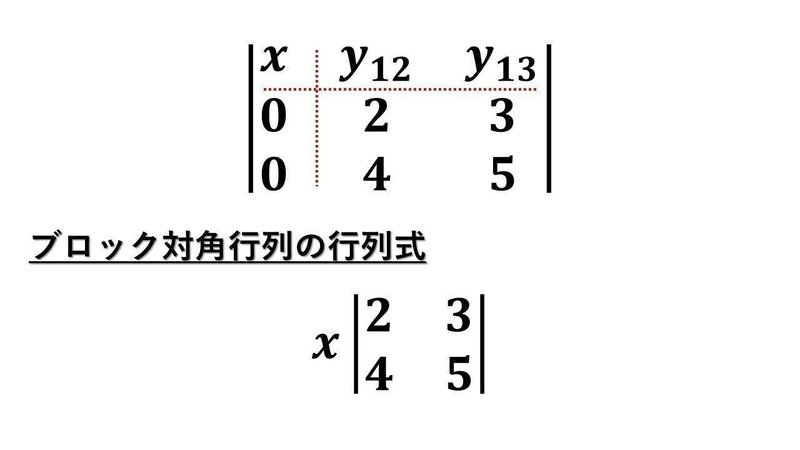
ブロック対角行列の行列式の計算
基本となる筋道を書いておきます。3行3列の行列式の2個目の対角上のブロック行列が2行2列なので、2行目と3行目の行ベクトルを考えます。
a[1] = (2, 3), a[2] = (4, 5) とおくと、
det(a[1], a[2])が2個目の対角上のブロック行列の行列式です。
単位ベクトルe[1] = (1, 0)とe[2] = (0, 1)の一次結合でa[1]とa[2]は表すことができます。
a[1] = 2e[1] + 3e[2],
a[2] = 4e[1] + 5e[2] となります。
e[1]とe[2]は一次独立なので、この一次結合の表し方は1通りのみということになります。ですので、写像detで移すことはwell-definedです。つまり、写像として、ちゃんと1対1対応するということです。
det(a[1], a[2])は、
det(2e[1] + 3e[2], 4e[1] + 5e[2])となっています。
線形性を使うチャンスです。
det(2e[1], 4e[1] + 5e[2])とdet(3e[2], 4e[1] + 5e[2])の和となります。
スカラー倍はdetの外に出るので、
2det(e[1], 4e[1] + 5e[2])と3det(e[2], 4e[1] + 5e[2])の和となります。
第2成分についても線形性を使うと、合計で4つの複素数の和となります。
2・4・det(e[1], e[1]), 2・5・det(e[1], e[2]),
3・4・det(e[2], e[1]), 3・5・det(e[2], e[2]) の4個の複素数の和となります。
detの交代性から、
det(e[1], e[1]) = 0, det(e[2], e[2]) = 0
なので、2個だけが残ります。
2・5・det(e[1], e[2]) + 3・4・det(e[2], e[1])
= 2・5・det(e[1], e[2]) - 3・4・det(e[1], e[2])
= det(e[1], e[2])(2・5 - 3・4)
ここで、det(e[1], e[2]) = 1 で、
2・5 - 3・4は2個目の対角上のブロック行列の行列式です。
ここまでの考え方は、2行2列の内容です。計算すべき行列式は3行3列です。この違いを修正するための工夫が必要になります。しかし、ちょっとしたことで、すぐに解消できます。
a[1]とa[2]という1行2列の行ベクトルから議論したけれど、1行3列の行ベクトルで議論すれば良いということです。

この図のはじめの行列式の式変形は何かということを説明します。
x[1]を与えられた3行3列の行列の1行目と同じ数字の並びの行ベクトルとします。
x[2] = (0, 2, 3),
x[3] = (0, 4, 5) とします。
det(x[1], x[2], x[3])が与えられた3行3列の行列式です。
単位ベクトルを同じeを使って書きますが、今度は3列あります。
e[2] = (0, 1, 0),
e[3] = (0, 0, 1) の一次結合でx[2]とx[3]を表します。
x[2] = 2e[2] + 3e[3],
x[3] = 4e[2] + 5e[3] として、
det(x[1], x[2], x[3])
= det(x[1], 2e[2] + 3e[3], 4e[2] + 5e[3]) について、3行3列の行列式の線形性と交代性を適用させると、先ほどと同じ式変形で、最後は
det(x[1], e[2], e[3])(2・5 - 3・4) となります。
ここまでを、行列表示している図で確認します。
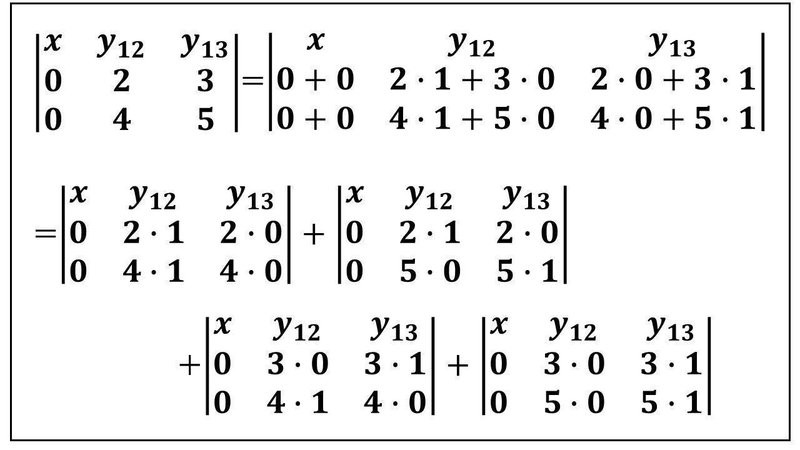
線形性から4個の行列式が出てきますが、交代性から、同じ成分の並びの行が2か所に出ると、行列式の値は0となりました。

0となって削除する2個が、この図の2個です。削除されずに残るのが次の図の2個の行列式になります。
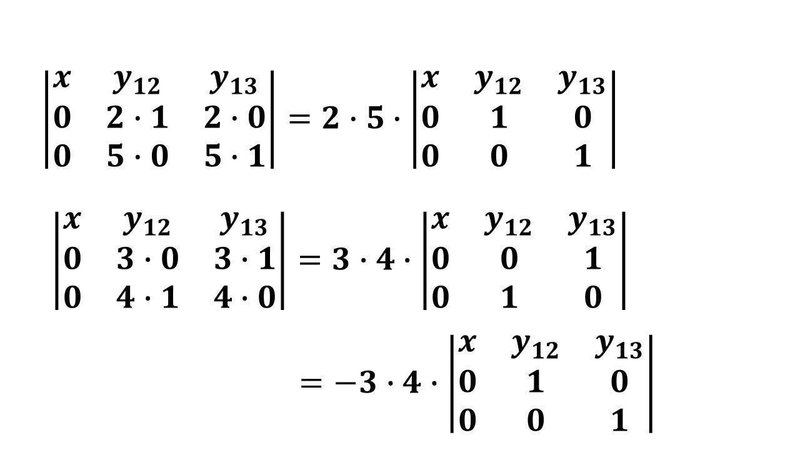
スカラー倍を行列式の外に出しました。最後の式変形は、2行目と3行目を入れ替えています。行列式の交代性から値は-1倍となります。
3・4・det(x[1], e[3], e[2])
= -3・4・det(x[1], e[2], e[3]) ということです。
では、求めたい行列式の値を計算します。残った2個の行列式をまとめます。

2つの項にはどちらにも同じ3行3列の行列式が掛けられています。
det(x[1], e[2], e[3])が、この3行3列の行列式です。
行列式の値は1つの複素数なので、複素数体における分配法則でくくり出します。
det(x[1], e[2], e[3])(2・5 - 3・4)が求める行列式の値です。
上三角行列の行列式なので、
det(x[1], e[2], e[3]) = x・1・1 = x と対角成分をすべて掛け合わせた値になります。
これで、赤で書いた等式が成立します。
実は、対角上の1つ目のブロック行列が1次正方行列でなくてm次正方行列で、2個目のブロック行列がn次正方行列となっているブロック対角行列になっていても、1行(m + n)列の行ベクトルについて、
det(x[1], ・・・, x[m], e[m + 1], ・・・, e[m + n])は、det(x[1], ・・・, x[m])と等しくなります。
行列式の定義から、1からmまでの自然数の並び替えによって現れる項でないと0となって消えることから導かれます。
関連するnote記事
行列式の余因子展開の練習として、4次正方行列の記事があります。ご興味がありましたら、お気軽にご覧ください。
▼4行4列の余因子展開
この記事が気に入ったらサポートをしてみませんか?
