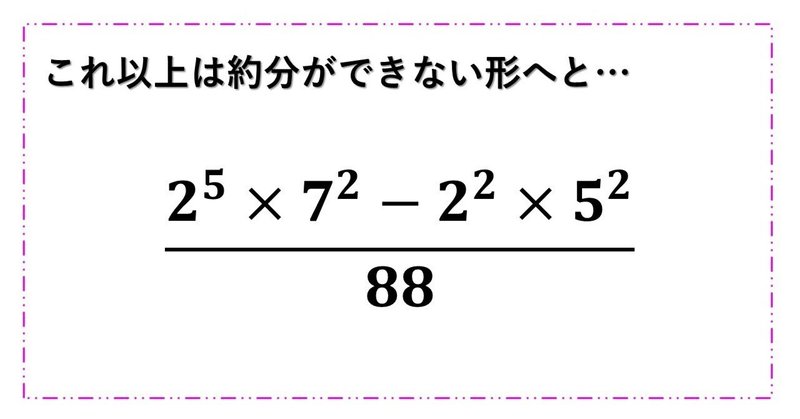
約分ができるのかどうか【分数についての問題】
中学の数学から指数が出てきます。この指数が分数の分母や分子に登場したときに、分数が約分できるのかどうかということを判断するのが苦しくなってきます。
中学一年の頃には、結構、この手の計算に苦戦するかもしれませんが、高校の数学や大学の数学でも分数と約分について考える場面があるので、良い練習になるかと思います。
中学一年の数学-発展的
$$
\displaystyle\frac{2^5\times 7^2-2^2\times 5^2}{88}
$$
この分数の分母と分子に登場している整数について、うまく約分ができるのかどうかを判断しながら計算を進めます。
分子を指数を使わない形にして、それぞれの引き算をすると、一つの整数として分子の数を表すことができます。しかし、それをするのは計算が大変そうな気がします。
こんなときに、計算の法則を利用しながら、分子と分母で約分をして、扱いやすい分数の形に書き換えたいところです。
計算の法則
素因数分解(すだれ算)と指数法則と分配法則が、よく使えます。
$$
\displaystyle\frac{2^5\times 7^2-2^2\times 5^2}{88}
$$
分子の引き算をする二つの項ですが、どちらも素因数分解された形で、素因数 $${2}$$ の指数乗は、くくり出すチャンスです。
このくくり出すときに、使うのが分配法則です。くくり出すときに、指数法則を使って、くくり出せるのが何乗までなのかを判断します。
$${2^5\times 7^2}$$ は $${2^2\times 2^3\times 7^2}$$ です。
指数法則を使うことで、分子について、$${2^2}$$ でくくり出せることが分かりました。
$$
\displaystyle\frac{2^5\times 7^2-2^2\times 5^2}{88}=\frac{2^2\times (2^3\times 7^2-5^2)}{88}
$$
素数たちの積の形で
分母の $${88}$$ について、素数たちの積の形で表してみます。この素数たちの積の形で表すことを素因数分解といいます。
$${88=2^3\times 11}$$
この素因数分解に現れている $${2}$$ と $${11}$$ という素数を $${88}$$ の素因数といいます。
これで、与えられた分数の式を次のように書き換えることができます。
$$
\displaystyle\frac{2^5\times 7^2-2^2\times 5^2}{88}=\frac{2^2\times (2^3\times 7^2-5^2)}{2^3\times 11}
$$
これで、分子と分母にともに $${2^2}$$ が掛けられていることが分かります。分母の $${2^3}$$ は $${2^2\times 2}$$ なので、$${2^2}$$ で分子と分母を約分できます。
$$
\displaystyle\frac{2^5\times 7^2-2^2\times 5^2}{88}=\frac{2^3\times 7^2-5^2}{2\times 11}
$$
ここまで、途中式をしっかりと書きましたが、慣れてくると、ここまでを暗算で変形できます。
素因数分解、指数法則、分配法則に慣れておくと計算が速く正確に実行できます。
分子が約分されて、計算しやすくなったので、分子を計算します。分母は素因数分解された形なので、分子を整理したあとに、$${2}$$ で約分できるのか、$${11}$$ で約分できるのかを判断するのに、このままで置いておきます。
$${2^3\times 7^2-5^2=8\times 7\times 7 -25}$$
$${=56\times 7-25=392-25}$$
$${=367}$$
これで、与えられた分数式は、
$$
\displaystyle\frac{2^5\times 7^2-2^2\times 5^2}{88}=\frac{367}{2\times 11}
$$
これ以上の約分できるかどうかの確認
$${367}$$ は奇数なので、$${2}$$ では割り切れません。
また、$${367= 33\times 11 +4}$$ なので、$${11}$$ でも割り切れません。
したがって、もうこれ以上は約分ができないことが分かりました。
$$
\displaystyle\frac{367}{22}
$$
これが、計算をして、もうこれ以上は約分ができない状態になった分数です。計算問題の答えとなる分数です。
ちなみに、もうこれ以上の約分ができない分数のことを既約分数といいます。
これで今回の note 記事を終了します。
ちなみに、高校の一年の数学計算を中心に書いたブログ記事がありまして、宜しければ、ご覧ください。iwai-math-blogというサイト内のブログ記事です。
この記事が気に入ったらサポートをしてみませんか?
