図式で学ぶ線形代数 #3 ~テンソル積およびトレース・転置・内積~
連載の記事一覧:
#1 図式の基礎と線形代数の基礎
#2 スペクトル分解と特異値分解
#3 テンソル積およびトレース・転置・内積
#4 行列が作るヒルベルト空間
番外編 列ベクトルや行列での微分
番外編その2 ベクトル解析
前回までは,主に行列の積に関する話題を中心に述べました。今回からは,行列のテンソル積を積極的に活用していきます。
('22/07/06:アダマール積のスライドを追加しました。)
テンソル積
テンソル積は,初学者にとってはやや難しい概念かもしれません。標準的な定義を眺めても,「なぜそのように定義されるのか?」などのいくつかの疑問を抱く人も少なくないと思います。これまではテンソル積の定義を明示的には示してきませんでしたが,今回の記事ではまずテンソル積空間の定義を示しながら,いくつかの補足をしておきます。
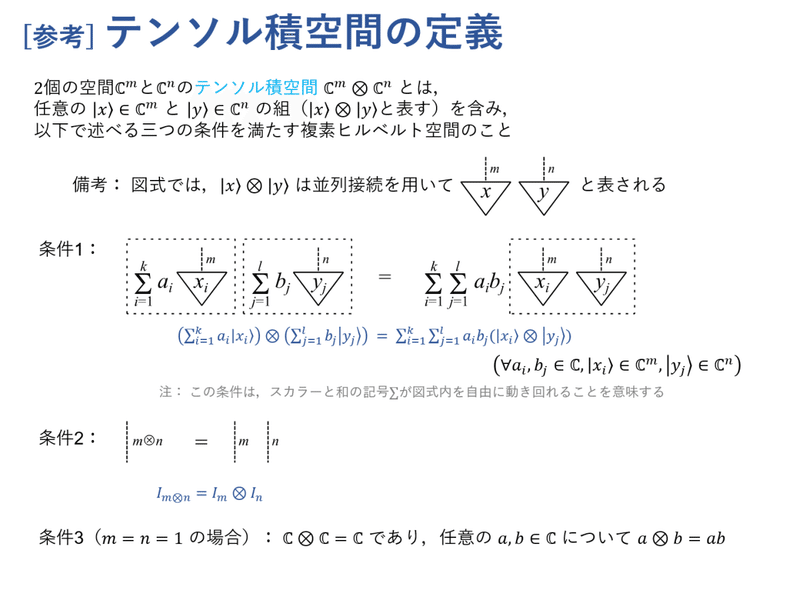
テンソル積空間 $${ \Complex^m \otimes \Complex^n }$$ は,直積集合 $${ \Complex^m \times \Complex^n }$$(つまり $${ \Complex^m }$$ の任意の要素 $${ \ket{x} }$$ と $${ \Complex^n }$$ の任意の要素 $${ \ket{y} }$$ の組 $${ (\ket{x},\ket{y}) }$$ をすべて集めた集合)に似て非なるものです。実際,$${ \Complex^m \otimes \Complex^n }$$ は複素ヒルベルト空間ですが $${ \Complex^m \times \Complex^n }$$ は複素ヒルベルト空間ではありません。大ざっぱな理解として,$${ \Complex^m \times \Complex^n }$$ を少し補正して複素ヒルベルト空間にしたものが $${ \Complex^m \otimes \Complex^n }$$ であると解釈するとよいと思います。
図式では,積を直列接続として表して,テンソル積を並列接続として表すのでした。ここで示した三つの条件は,「複素ヒルベルト空間の『並列接続』として満たしてほしい条件を明記したもの」と解釈できます。条件1より,例えば $${ (2\ket{x}) \otimes \ket{y} }$$ と $${ \ket{x} \otimes (2\ket{y}) }$$ は同一視されます(これらは $${ 2 (\ket{x} \otimes \ket{y}) }$$ とも同じです)。このことは,直積集合の要素 $${ (2\ket{x}, \ket{y}) }$$ と $${ (\ket{x}, 2\ket{y}) }$$ が区別されることとは対照的です。条件2は,$${ \Complex^m \otimes \Complex^n }$$ に対して「何もしない」ことは,$${ \Complex^m }$$ と $${ \Complex^n }$$ の両方に対して「何もしない」ことに等しいことを表しています(恒等写像 $${ I }$$ は「何もしない」写像とみなせます)。条件3は,スカラー同士のテンソル積は積に等しいことを意味しています。
なお,条件2では行列のテンソル積を用いています。行列のテンソル積は,連載第1回のスライド「行列の積とテンソル積」で述べた式 $${ (X_1Y_1) \otimes (X_2Y_2)= (X_1 \otimes X_2) (Y_1 \otimes Y_2) }$$ を満たすようなものとして定義できます。
ここで紹介したテンソル積空間の定義は,標準的なテンソル積の定義と本質的に等価です。なお,本書(=今秋出版予定の書籍)では,標準的な定義の一つを採用して「双線形写像」という視点から定義しています。テンソル積については,複数の定義に触れることでよりしっかりと理解できるようになるはずです。ここで紹介した「テンソル積とは並列接続のこと」という考え方は,より素直に理解するための助けになると思います。
なお,本連載では並列接続を「テンソル積」とみなしていますが,「直和」とみなすような図式も考えられます("Graphical Linear Algebra" のようによばれるようです)。量子論の場合には,「テンソル積」とみなしたほうが便利な場面が多いと思います。
cup列ベクトルとcap行ベクトル

まずは特別な列ベクトルと行ベクトルを定義します。図式ではこれらを $${ \cup }$$ および $${ \cap }$$ のような特別な形で表し,それぞれcup列ベクトルおよびcap行ベクトルとよぶことにします。なお,記号 $${ \cup }$$ および $${ \cap }$$ がそれぞれ cup および cap とよばれることから,このように命名しています。
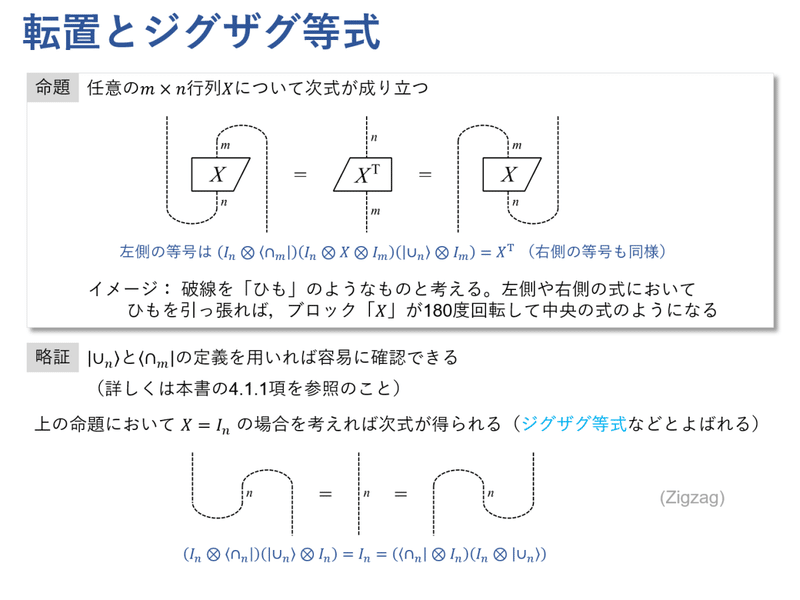
転置は,cup列ベクトルとcap行ベクトルを用いて表せます。連載第1回では転置を「180度回転」に対応付けましたが,その理由はこの命題からわかると思います。
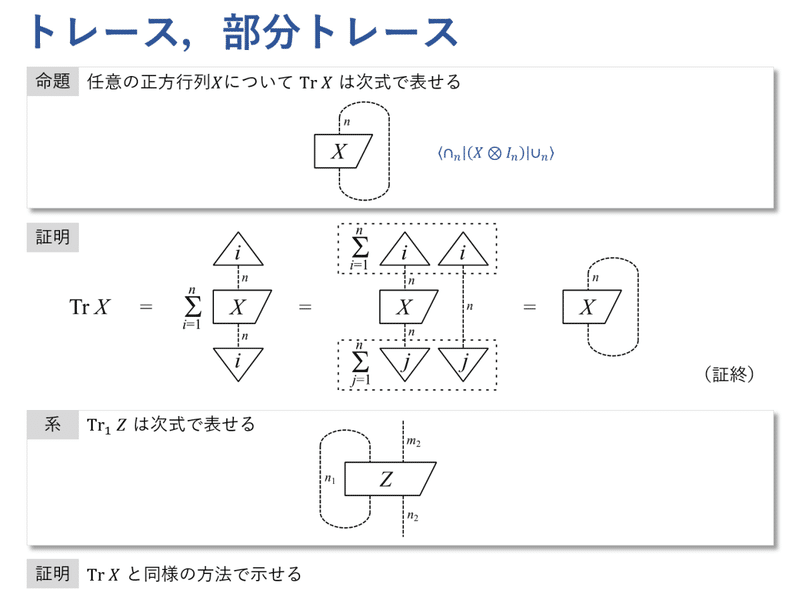
トレースは,cup列ベクトルとcap行ベクトルを用いて表現できます。まるで入力と出力を1本の「ひも」でつないだかのような図式になっていますが,この図式がトレースの理解を助けます。
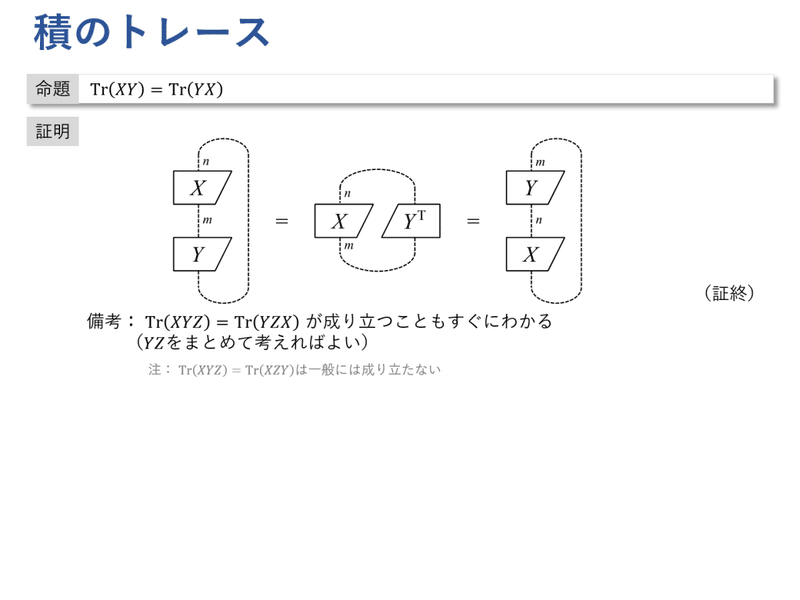
$${ \mathrm{Tr}(XY) = \mathrm{Tr}(YX) }$$ が成り立つことは,図式を眺めれば明らかです。ブロック $${ Y }$$ が「ひも」に沿って動いていると考えると,直観的に理解できると思います。
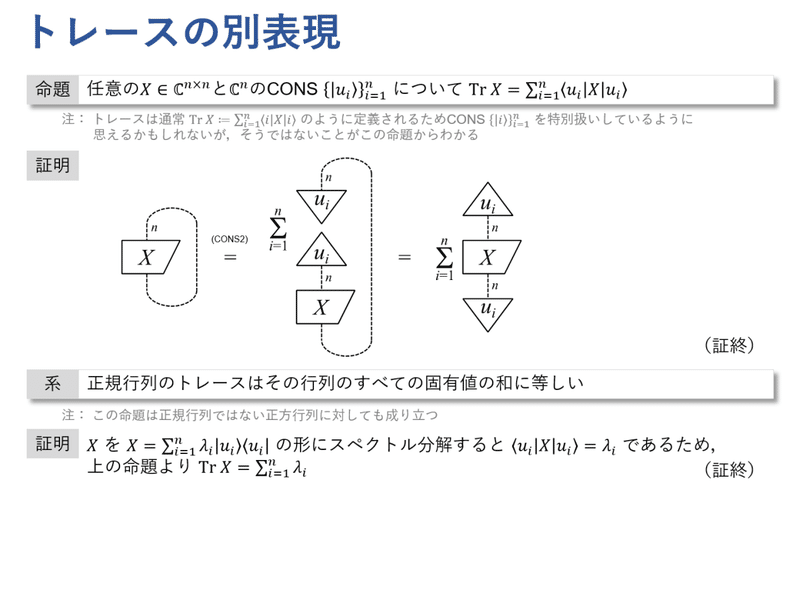
この命題では,トレースが「任意に選んだCONS $${ \{ \ket{u_i} \} }$$ でみたときの対角成分の和」に等しいことを主張しています。系より,「固有値の和」にも等しいことがわかります。
なお,トレースとは対照的に,行列式はこれまでに紹介した図式では簡単には表せません。行列式のように,図式よりも数式を使ったほうが表現しやすい場合もありますので,両者を使い分けるとよいと思います。ちなみに,行列式 $${ \mathrm{det} }$$ は $${ \mathrm{det} := \exp \circ \mathrm{Tr} \circ \exp^{-1} }$$ として定義できます。(ただし,$${ \exp^{-1} = \log }$$ です。また,$${ \exp^{-1} 0 }$$ は定義されないため,$${ 0 }$$ は特別扱いして $${ \det 0 = 0 }$$ と考えます。)
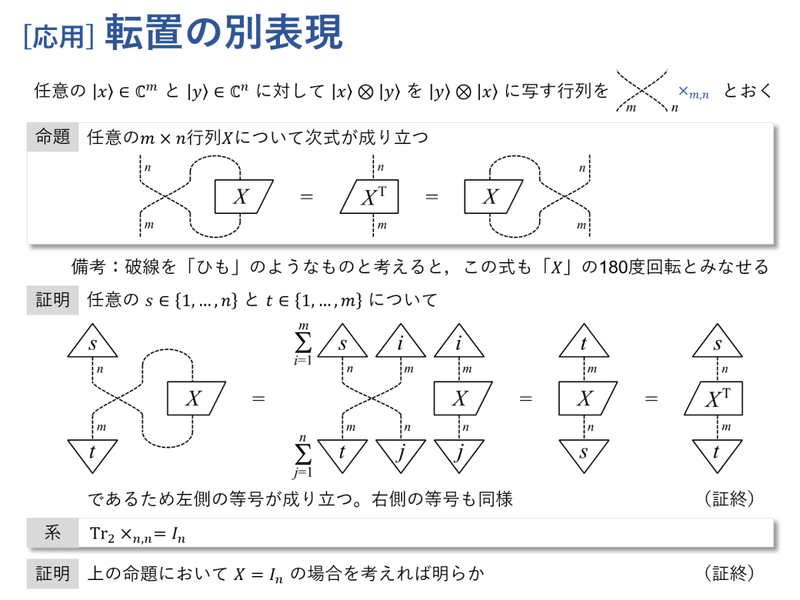
転置の別表現です。先に示した表現と同じものを表していることが直観的にわかると思います。
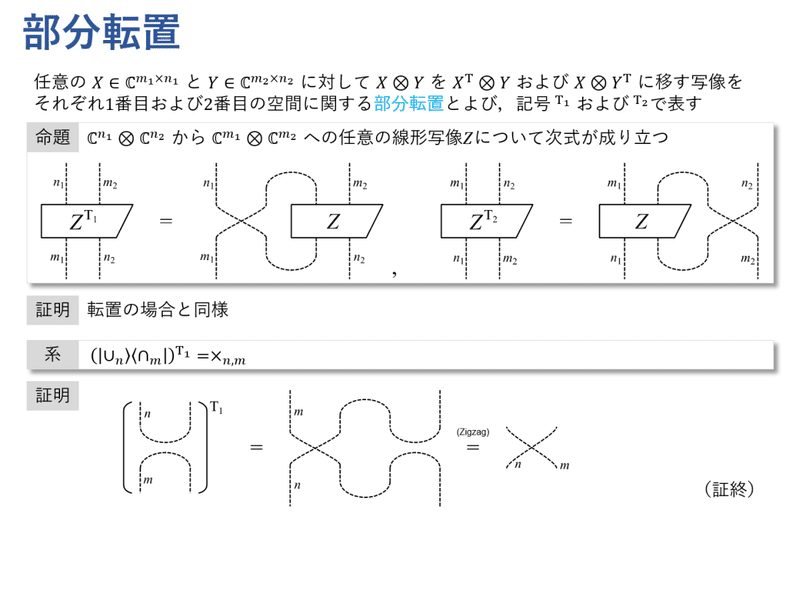
部分転置も,転置と同様に表現できます。
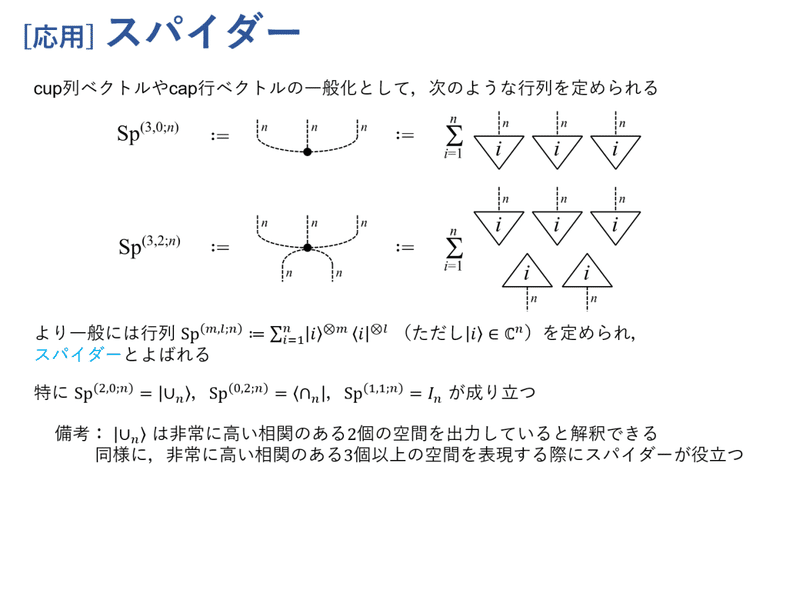
cup列ベクトルとcap行ベクトルを一般化した概念として,スパイダーがあります。量子回路の制御ゲートで現れる「黒丸」はスパイダーとみなせます。スパイダーは,3個以上の量子系のもつれ状態(例えばGHZ状態)を扱う際などにもしばしば使われます。
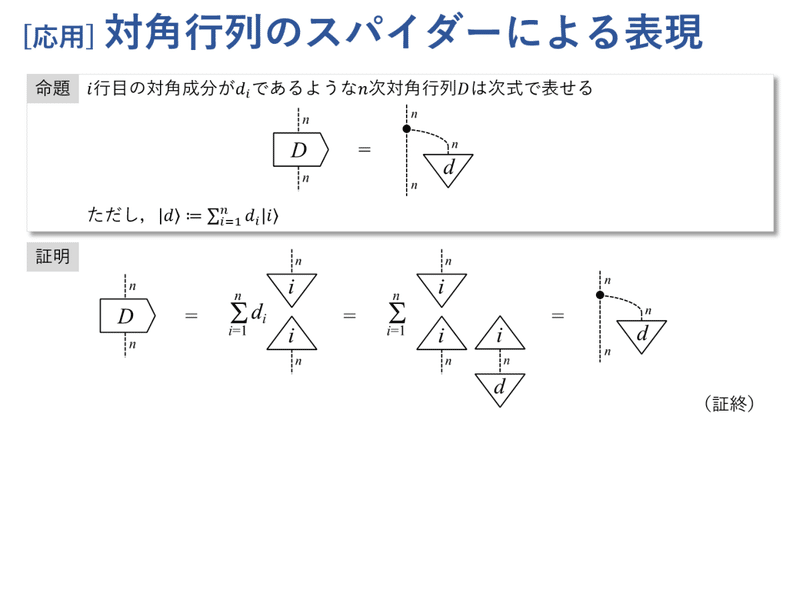
スパイダーを用いると,対角行列を比較的簡単な図式で表せます。
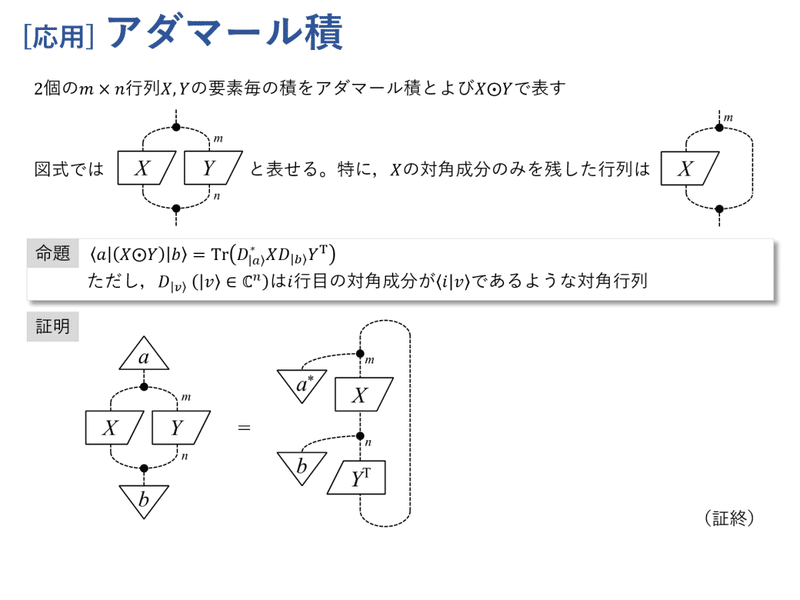
アダマール積(行列の成分毎の積)は,スパイダーを用いて表せます。
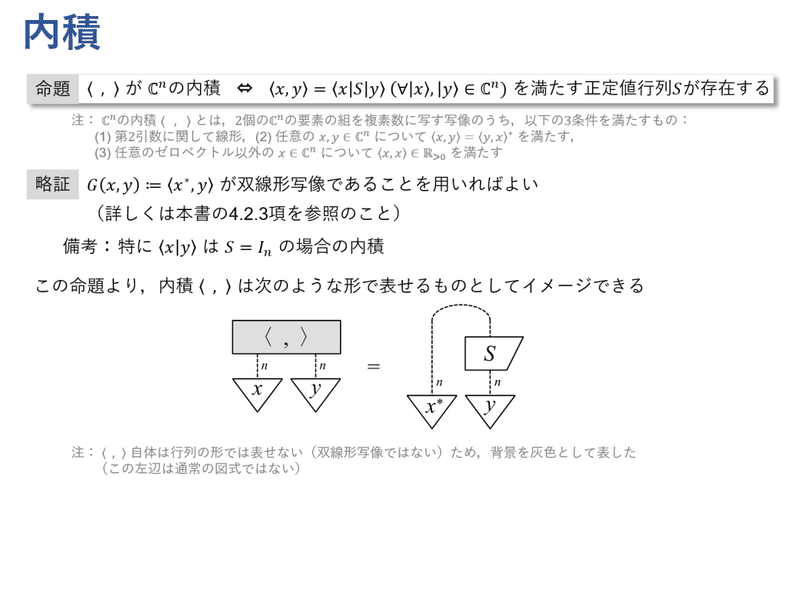
内積と正定値行列は一対一に対応しています。複素空間の場合,内積そのものは双線形写像ではありませんので通常のブロックでは表せませんが,一応図式を使って表現できます。実空間の場合には,内積は双線形写像であり,行ベクトルを用いて表せます。
今回はcup列ベクトル・cap行ベクトルの基礎について述べました。次回は,これらの概念を用いると行列をベクトルとして自然に扱うための方法などを説明する予定です。
この記事は,書籍「図式と操作的確率論による量子論」の内容の一部を紹介したものです(この記事のほうが詳しく述べている箇所もあります)。
この記事が気に入ったらサポートをしてみませんか?
