書籍「図式と操作的確率論による量子論」の紹介記事です。今回は，「図式」について説明します。

連載の記事一覧：
#1 目的や特徴
#2 図式とは
#3 操作的確率論とは
#4 標準的な量子論の書籍との違い
番外編 ～初学者向け資料～

図式とは何か

図式とは，線形代数などに関する数式と同じ内容のものを図形により表現したものです。厳密性を保ったまま表現でき，（数式と同じく）図式のみを用いて計算できます。量子回路やテンソルネットワークの図をご存知の方はイメージしやすいかもしれません。これらの図は図式の一種とみなすことができます。

図式を用いることの利点

以下の二つです。

1. 数式よりも直観的に表現できる場合が多々ある。

2. 数式では隠れてしまいがちな本質的な事柄をしばしば顕在化できる。

とくに，合成系に関する式では，数式よりも図式のほうが直観的で簡単に描ける場合が多くあります。量子論の初学者でも，はじめから図式を用いて直観的に捉える方法を学んでおくとよいと思います。

図式の例

ここでは主要な例を紹介します。初学者や図式の読み方を知らない方にとっては難しい例ばかりかと思いますが，わからなくても気にせずに雰囲気をつかんでいただければ幸いです。

例1：量子操作の表現

すべての量子操作 $${ f }$$ は，「入力と純粋状態 $${ \ket{\psi} }$$ との並列接続にユニタリ変換 $${ U }$$ を施した後で部分系（$${ D }$$ とおくことにします）を捨てる」という操作の形で表せることが知られています。この表現は，シュタインスプリング表現とよばれています。これを数式で表すと次のようになります。

$$
f(\rho) = \mathrm{Tr}_D [U(\rho \otimes \ket{\psi} \bra{\psi}) U^\dagger]
$$

図式では次のように表せます。

図式では，$${ f }$$ の入力および出力をそれぞれラベル $${ A }$$ および $${ B }$$ が付いた線として表しています。図式は，図の下側から上側に向かって情報が流れるようなイメージで眺めるとわかりやすいと思います。また，右辺の右上に描かれた3本の横線は，「系を捨てる」ことを表しています。

これらの式を比べると，図式のほうがより直観的に表現できていると感じるのではないでしょうか。数式では基本的に式を横方向に書くため「$${ 1 }$$ 次元的」であるのに対し，図式では横方向と縦方向を使って「$${ 2 }$$ 次元的」に表せていることがわかります。このため，縦方向を効果的に使える図式のほうが数式よりも見やすくなることが多々あるのです。少し慣れれば，図式のほうが早くかつ素直に理解できるようになると思います。

例2：量子テレポーテーション

二人（アリスとボブとよぶ）の間で事前にある特定の量子状態 $${ \sigma }$$ を共有していれば，アリスのみがもっているある系 $${ A }$$ の任意の量子状態 $${ \rho }$$ を古典通信のみでボブに転送できることが知られています。この転送は量子テレポーテーションとよばれています。量子テレポーテーションが実現できることを数式で示すことはそれほど容易ではないのですが，次の図式を用いれば比較的容易に説明できます。

ここで，古典系 $${ C }$$ をとおして古典通信を行っています。完全に理解してもらうためにはいくつかの補足が必要なため，ここで詳しい説明をすることは控えます（本書の8.2.4項で説明しています）。しかし，図式に慣れればこの図式で本質が伝えられていることがわかるようになります。

なお，上の図式では状態 $${ \sigma }$$ をアリスとボブで共有していることやプロセス $${ \Pi }$$ の出力が古典系 $${ C }$$ であることを視覚的に表しています。このように，図式では多くの情報を瞬時に伝えられるという利点もあります。

例3：CP写像のクラウス表現

量子論では完全正値写像（CP写像）とよばれる線形写像が頻繁に現れ，量子論を十分に理解するためにはCP写像について詳しく知ることが重要です。線形写像 $${ f }$$ がCP写像であるならば $${ f }$$ がクラウス表現とよばれる表現ができるのですが，このことを直観的な形で理解しておくと多くの場面で役に立つと思います。CP写像がクラウス表現できることを数式により示そうとするとなかなか難しいのですが，次のような図式を用いると直観的な形ですぐに示せます。

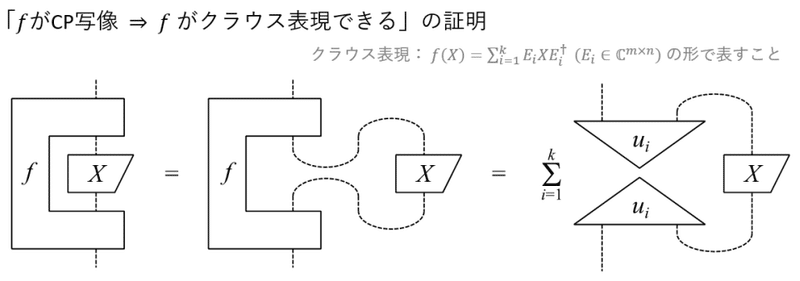
この図式の意味はここでは説明しませんが，一度図式に慣れてしまえばすぐにわかるようになります（詳細は本書の4.4.2項と4.4.3項で説明しています）。図式のほうが直観的である理由は，CP写像がもっている本質的な性質を顕在化できているためといえそうです。

その他の例

「図式で学ぶ線形代数」や「図式で学ぶ量子論」に，図式の例が多く載っています。これらを眺めていただければ雰囲気がつかめると思います。

ここで紹介した例は比較的単純なものばかりでしたが，よりプロセス数が多くそれらが複雑に接続するほど，一般に数式と比べて図式のほうが見通しがよくなります。