この記事は，以下の記事で述べた位相空間に関する記事です．

第1節　数学の3つの柱と位相空間論の役割

　大学の数学科で学ぶ数学には，実に様々な分野があります．それらは主に次の3つの分野に類別されることが多いです．　

【解析】

【代数】

【幾何】

　純粋数学は，厳密な論理を土台として展開されます．解析・代数・幾何，それぞれの分野にも特有の論理の土台が存在します．解析なら実数や微分などの論理，代数であれば群や環の論理，そして幾何なら空間の論理などです．

　位相空間は幾何学を展開する上で最も基本的なものである連続概念の論理的な部分を扱う分野であると言えます．

　空間の中では，連続変形や微分積分など様々なことが行われます．そのなかでも空間の連続性に着目し，それを突き詰めて考えていくと出てくるのが位相空間という考え方です．

　私たちが空間を思いうかべるとき，そこには必ず連続という考え方があります．空間の中で図形を「連続的に動かす」とかグラフが「連続的につながっている」などなど．

　位相空間論では，私たちが思い浮かべる【空間】から，連続概念の根元となる部分だけを取り出してそれを考察します．

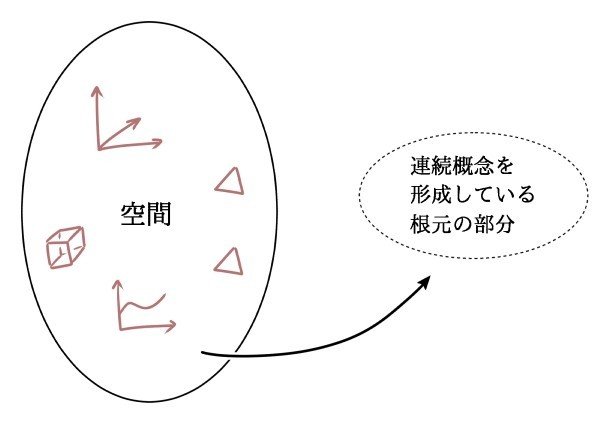
　この根元の部分は位相(topology)とよばれるものです．

　位相空間論の難しさは，なんと言ってもその抽象性にあります．

　位相空間論では，連続概念に対する純粋論理的で根源的な話が展開されるため，連続に関する直観はすべて排除しなければいけません．「途切れなく続いているさま」を連続という言葉のイメージには使えないのです．

　実際，連続概念を形成している部分(位相)を別のものにすることによって，私たちが普段思い描く空間とはまったく違った連続概念を持つ空間も得られます．後に記述するように，実数直線にいつもと違う位相を与えることで， f(x) = cos x などがが不連続関数として扱われるということが起こりえます．

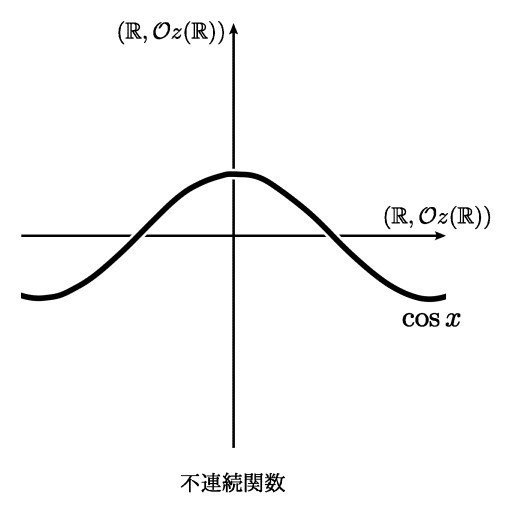
　( Oz(R) というのが実数 R に与えられた，ある特別な位相を指しています．）

　位相空間論は幾何学といいながら，扱う対象を図に描くということをあまりしないのです．なぜなら，例えペンを滑らかに滑らせて描いた図形であっても位相空間論においては連続的なものを表しているとは限らないからです（抽象的な図は結構描きますが，それを論理展開にそのまま使うことはありません）．

　したがって，位相空間論では幾何学的な内容がすべて論理式によって展開されていきます．高校までで養われた幾何学のイメージが根底から崩れるわけです．

　そんなこんなで，位相空間論で躓いてしまう学生は後をたたないわけです．

　以下では，そんな位相空間論について少し細かいところまで説明しています．位相空間ってだいたいこんなもんかー，で済ませたい人はここまで読んでいただければ十分です．

第2節　連続概念を支えているものとは何か

　2.1 連続の定義

　位相空間は純粋数学における幾何学において，なくてはならないものです．ではそもそも位相空間とは具体的にどのようなものなのでしょうか？

　位相空間とは簡単に言うと，連続という概念を扱うために最低限必要な土台です．連続関数とか，図形が連続的につながっている（連結である）といった概念を扱うために最低限必要な構造を持った数学的対象が位相空間です．

　この位相空間，何が難しいのかと言うと，とにかく抽象的で何のために存在しているのかがわかりにくい概念なのです．その話をする前に高校数学における連続の扱われ方をみてみましょう．

　高校数学において，連続という言葉は主に関数に対して使われています．関数が連続であることは極限によって表されていました．

　大学数学においては，連続関数はイプシロン-デルタ論法によって論理式による厳密な定式化がなされます．これは，数学科の学部生にとって最初の関門でしょう．

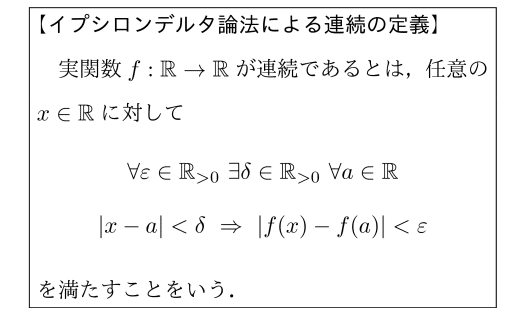
　途中に現れる論理式はすんなり理解できるようなものではありません．訓練を積んで，論理式という数学言語に対する慣れを身に着けていくしかないのです．

　このイプシロン－デルタ論法は純粋数学の厳密な議論の難しさを物語るものとして，大学数学の中では有名なものです．

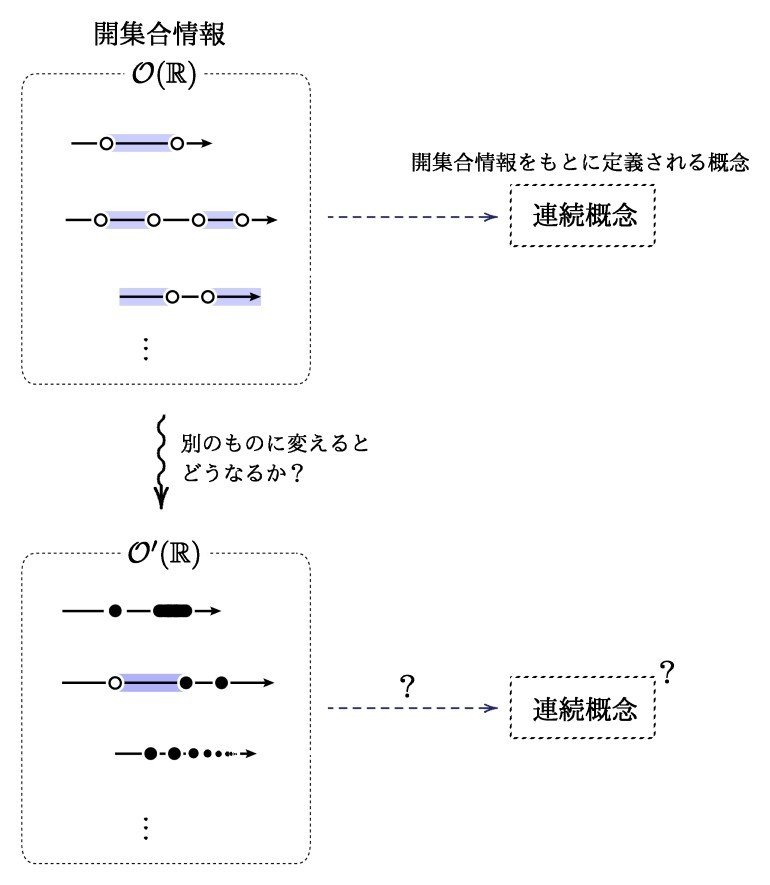
　しかし，数学科で学ぶ学生は，これよりも，もっと洗練された連続の定義を学びます．それは“開集合“というものを使ったものであり，これこそが位相空間の概念の始まりになります．

　2.2 開集合

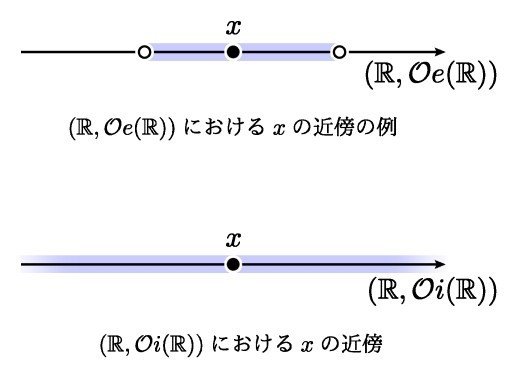
　空間上の点 x に着目するとき，その周りに x の近傍というものを考えることができます．

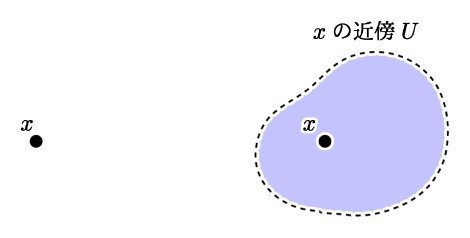
　この x の近傍という概念は，ある x の近くにどんな点があるのかなどを記述するものになっています．そして【 x の近傍】とは x を含むような開集合として定義されます．開集合は空間内のいたるところに存在しており，【ある点の近傍】であったり，あるいは複数の点のおぼろげな離れ具合を表すものであると解釈できます．

　空間には必ずこういった開集合というものを考えることができます．そうでなければ点と点の近さという概念自体が意味をなさなくなってしまうのです．そして　連続という概念はこの開集合という概念だけを用いて定義することが可能です．

　細かい単語の意味は専門的になっており，知識がなければ正確に読むことは困難ですが，さきほどのイプシロン-デルタ論法に比べると非常に簡潔な定義になっていることだけは読み取れるかと思います．

　この定義において重要なことは，連続という概念は開集合さえあれば定義できるということです．（イプシロン-デルタ論法の定義には |x-a| などの式が用いられていました．）　言うなら，

「連続の理論は開集合の理論である」

となるでしょう．開集合は空間における【近さ】を表すための役割だけではなく，連続概念の基礎部分をなしている重要なものだったのです．

第3節　開集合自体を変える

　3.1 ユークリッド空間

　連続の定義が書き換わったとは言え，連続の意味することは変わってはいません．依然として f(x)=x² は連続関数として扱えますし，途中で途切れてしまうような関数は不連続関数になります．

　しかし連続関数が開集合のみで定義されることがわかったおかげで，理論展開の視野が広がっています．

　わたしたちは普通，空間と言ったらこの世界をイメージします．立体図形などを置くことのできる場所，それが空間です．数学において，そのような普通の空間は【ユークリッド空間】と呼ばれています．

　ユークリッド空間において，開集合とは境界のない領域として表現されます．そしてそれは空間内のいたるところに存在しています．

　いま，この図は平面を表していますが，数学では1次元，2次元のものも【空間】という言葉で統一してしまうことが多々あります．

　以降の話では，簡単にユークリッド直線を考えることにします．これはいわゆる実数直線ともよばれるもので，

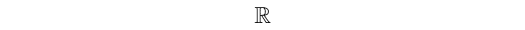
という記号で（いまのところ）表されます．

　このユークリッド直線における開集合とは，いわゆる開区間やそれらの和集合のことです．

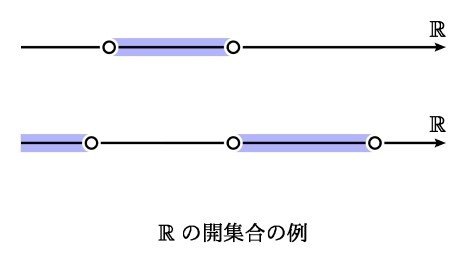
　これら開区間やその和集合を【 R 上の開集合】と呼ぶことにしましょう．この R 上の開集合をすべて集めてできる集合

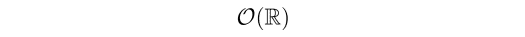
がユークリッド直線上の関数などの連続概念の土台になっているのです．

　3.2 抽象的な考え方の始まり

　連続概念は開集合によって記述できるということは先に述べたとおりです．では，開集合そのものが別のものに変わってしまったらどうなるでしょうか？

　まず，開集合が変わるとはどういうことかを説明しなければいけません．

　何度も言うように，開集合は連続概念を支える土台としての役割を持っており，そして連続概念は空間を空間足らしめているものです．連続であるという概念がなければ空間は意味をなしません．

　例えば実数の集合 R は「R上の開集合とは何か？」の情報がなければ ，何の意味もない存在なのです．純粋数学において集合は記号の集まりとしての役割しか持っていないからです．例えば「点 1 ∈ R の近くにはどのような点が存在するか？」　と問われても，開集合が何かが定められていなければ答えられないのです．

　R はそれ単体では空間とは呼べず， R に開集合の情報

を与えて初めて R は空間と呼べるものになります．O(R) は【 R の開集合族】（あるいはR の位相，R のトポロジー）と呼ばれます．これら R と O(R) の組

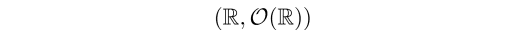
がユークリッド直線とよばれているものだったのです．

　ではこの開集合の情報 O(R) とはどのように与えられるものなのでしょうか？　適当に与えてしまってよいのでしょうか？　ユークリッド直線 (R,O(R)) に話を限れば，O(R) はユークリッド距離というものによって与えられています．しかし，このユークリッド距離も R とは独立に与えられているものです．

　すなわち，R 上の開集合が，開区間とその和集合で与えられるべき絶対的な理由は存在しません．

　言い換えれば，R上の開集合というのは，集合 R から自然発生的に得られるものではなく，したがって集合 R とは独立に存在しているものと考えられます．

　つまり開集合の情報を何か別のものに置き換えても，わたしたちがユークリッド平面で営んできた連続概念の議論は同じように展開できるかもしれないのです．

第4節　開集合が別のものに変わった世界

　4.1 開集合と呼ばれるための条件

　いままで O(R) は【R 上の開区間とその和集合】をすべて集めてきたような集合でしたが，この O(R) を別のものに変えてしまっても，それを土台とする連続概念は意味のあるものになってくれるのでしょうか？

　一般には，O(R) をメチャクチャなものに変えてしまうと連続の概念はうまく機能してくれません．すなわち O(R) は R の開集合族とは呼べるものではなくなってしまうのです．

　そこで，連続理論がユークリッド幾何の場合と同様にできるような条件が O(R) には必要です．その条件は様々な形で表されますが，現代数学では以下のようなものが主流になっています．

(条件1) 開集合の和集合は再び開集合にならなければならない．

(条件2) 開集合の共通部分は再び開集合にならなければならない．

　数学科の学生用に，ちゃんとした文章でも書いておきましょう．

　以上の3条件を満たすようなものはすべて連続概念の土台としての R の開集合族になりえるのです．

　4.2 (R,O(R))の例

　具体的にどのようなものがあるでしょうか？　大学では主に次のような例が挙げられるでしょう．

例1　開集合が空集合と全体集合 R のみからなるもの

　まず極端な例としては O(R) を次のようなものとします．

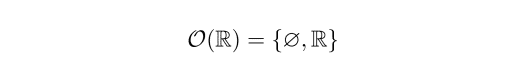
この O(R) はさきほどの２条件を満たしています．すなわちこの O(R) も連続概念を展開させるための土台として有効なものになっているのです．

　ユークリッド直線のときと区別するために，この O(R) を

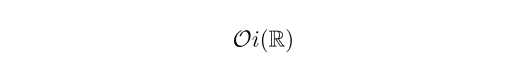
と書き，ユークリッド直線に定められたものを

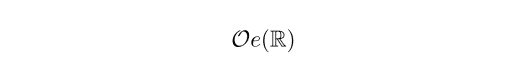
と書きます．

　(R,Oi(R)) の世界では，開集合は空集合と全体集合しかありません．したがってユークリッド直線 (R.Oe(R)) において開集合であったものも， (R,Oi(R)) では開集合になるとは限りません．

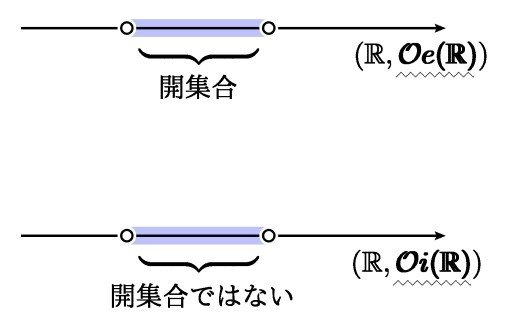
　開集合とは点どうしの近さをあらわすものであることを念頭に，開集合が2つしかないということの意味をイメージしてみます．

　例えば「点 x ∈ R の近くにはどんな点がありますか」と質問した場合，x を含むような開集合は全体集合しかありませんから，この世界ではすべての点が一様に x に近いということになります．

　そんな理由から，(R,Oi(R))は【密着空間】ともよばれます．

例2　開集合が R のすべての部分集合からなるもの

　次の例は，すべての R の部分集合が開集合となるような世界です．すなわち

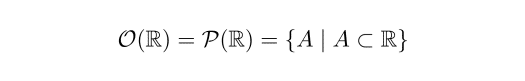
　です．この O(R) を

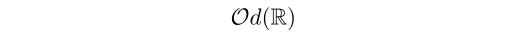
と表記することにします．

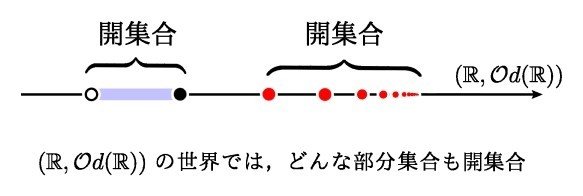
　この世界では点 x ∈ R の近くをあらわす開集合はたくさんとれますが，その中でも一番小さいものは {x} です．すなわち x だけからなる集合が x の近傍としてとれます．

　これが何を意味しているのかと言うと， x は他の点から遠い存在であるということです．ちょっと図を大げさに描くとこうなるでしょう．

　したがってこの世界 (R,Od(R)) では，すべての点が一様に離れているため，【離散空間】とも呼ばれます．

例3　開集合が補有限集合となるもの

　整数論等において重要となる世界として，開集合が次のような形のものがあります．

　この場合の (R,Oz(R)) は代数的な対象（多項式や有理式）を扱うのに都合のいい世界になっています．

　4.3 異世界での連続関数

　さて，いくつか例を挙げましたが，これらの世界での連続関数はユークリッド直線で扱ってきたものとは全く異なるものになっています．

　ユークリッド直線のときの，連続の定義を再掲してみましょう．

開集合が別のものに変わった実数直線上の連続関数の定義もこれと同じように行われます．

どちらも開集合によって連続が定義されています．

　例えば，定義域が (R,Oi(R)) で値域が (R,Oe(R)) のときは定数関数しか連続関数になってくれません．g(x)=x² や h(x)=sin x などは連続関数になってくれないのです．つまりこの文脈において，g(x) や h(x) のようなものは不自然な存在ということになります．

　また，例えば定義域が (R,Oz(R)) で値域が (R,Oz(R)) の場合，ある種の多項式関数 f : R → R は連続になってくれます．

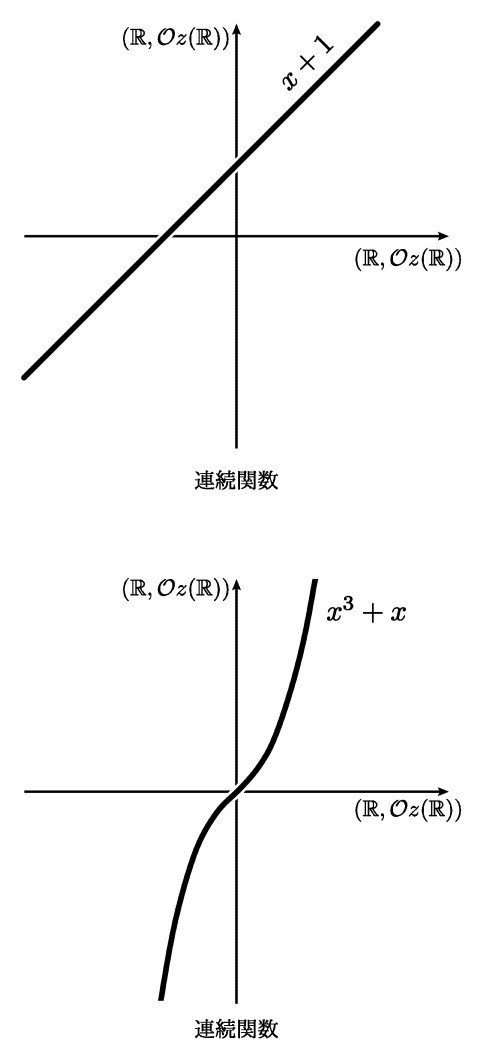
　しかし，cos x などは連続関数になってくれません．

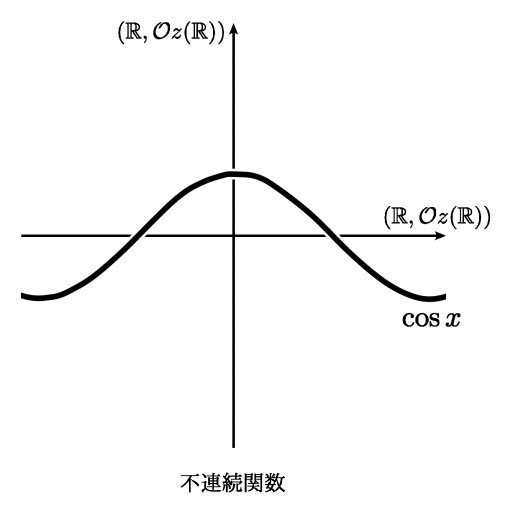
　(R,Oz(R)) は，多項式関数のように代数的なものが他の cos x, sin x などの関数よりも強調されている世界なのです（複素数のような代数閉体とよばれるものの上でより有効にはたらきます）．

　この Oz(R) のような開集合系の考え方は代数幾何学という分野において重要な役割を果たします．

第5節　どんな集合も空間になり得る

　以上の話では，実数の集合 R を土台にして，そこに開集合 O(R) というものを与えることで，連続概念を扱う土台となる空間 (R,O(R)) を構築しましたが，このようなプロセスは R に限らず，どんな集合の上でも行うことができます．

　いま，任意の集合 A が与えられているとしましょう．すると R のときと同じように A の部分集合を集めた集合 O が開集合と呼ばれるための条件さえ満たせば， A において連続概念が使えるようになるのです．

　開集合となるための条件は，R のときと変わりません．一応再掲しておきましょう．

　　したがって，どんな集合 A も，開集合族の条件を満たす O を兼ね備えていれば連続概念が意味を持ち，したがって A と O は空間としての役割を持ちます．

　このような A と O の組 (A,O) は【位相空間】と呼ばれます．

　例えば，2つの集合 A,B を

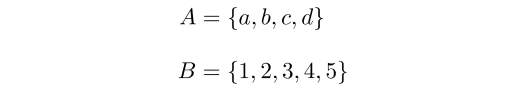
として，それぞれに開集合を次のように定めてみましょう．

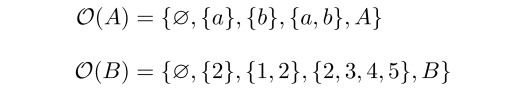
　これによって，(A,O(A)), (B,O(B)) はそれぞれ位相空間になります． 例えば A の方で a ∈ A を含む開集合（ a の近傍 ) は何かと聞かれたら {a} や {a,b} であると答えられますし， c ∈ A の近傍は全体集合 A のみであると答えられます．

　(A,O(A)),(B,O(B)) は空間なので連続概念が意味をなします．例えば定義域が (A,O(A)) で値域が (B,O(B)) の場合，連続関数 f : A → B の例として以下のようなものがあります．

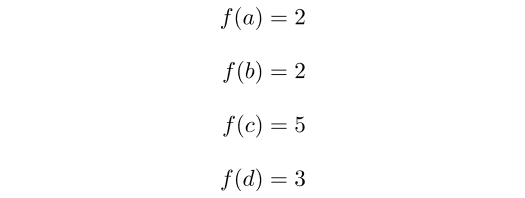
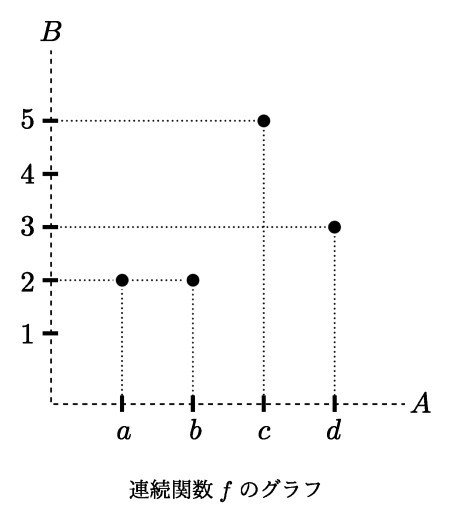
　このグラフはかなり模式的な図ではありますが，ユークリッド直線上の連続関数と比べてみましょう．

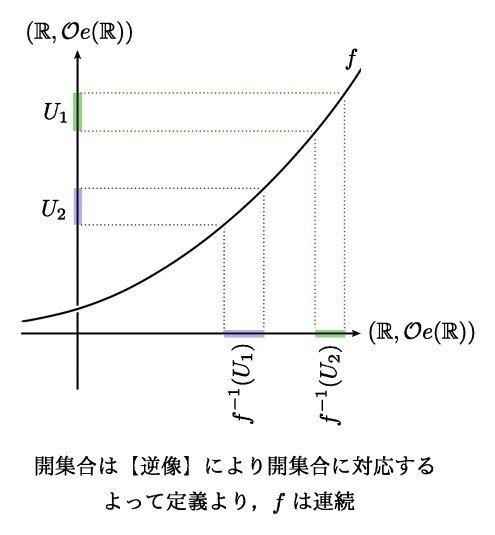
　また，次のような写像は f : A → B はいまの文脈においては連続関数になりません．

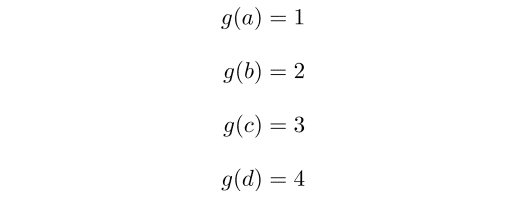
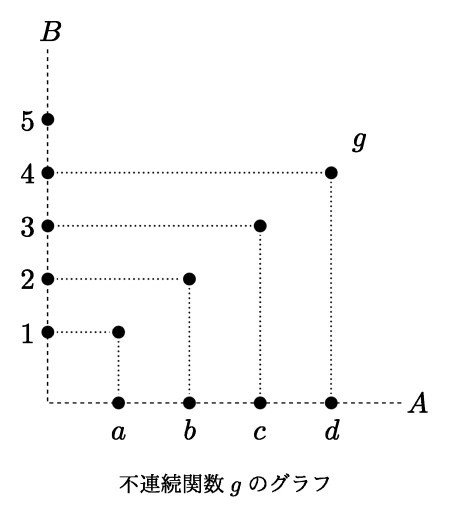
　例えば {2,3,4,5} という B上の開集合に対して，その逆像は {b,c,d} であり，これは A上の開集合になっていないからです．数式で書くと

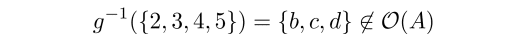
です．

　このように，どんな集合でも，開集合の情報を何かしら与えることによってそれを空間にすることが可能になります．

第6節　位相空間の考え方が必要になるとき

開集合の情報をもともとの集合と分離して考えることによって，【同相】の考え方が簡潔になされるようになります．

　【同相】とは，2つの位相空間の間に定義される概念です．例えば (A,O(A)) と (B,O(B)) は，見た目が違っても空間としては同じものを表しているということがよくあります．

　例えば，このような例を考えてみると分かりやすいかもしれません．

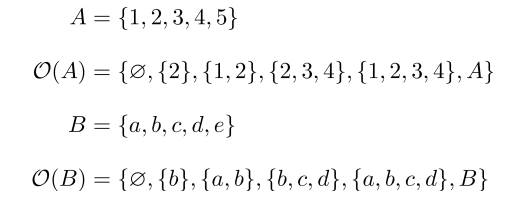
以上の例では集合 A,B に使われている記号は違いますが，開集合の見た目はまったくおなじになっています．すなわち A,B は空間としては全く同じものを表しているのです．

　このように2つの位相空間は，(大雑把に言うと）それぞれの集合の点が一対一に対応し，かつその上の開集合も一対一に対応しているようなときに同相と呼ばれます．

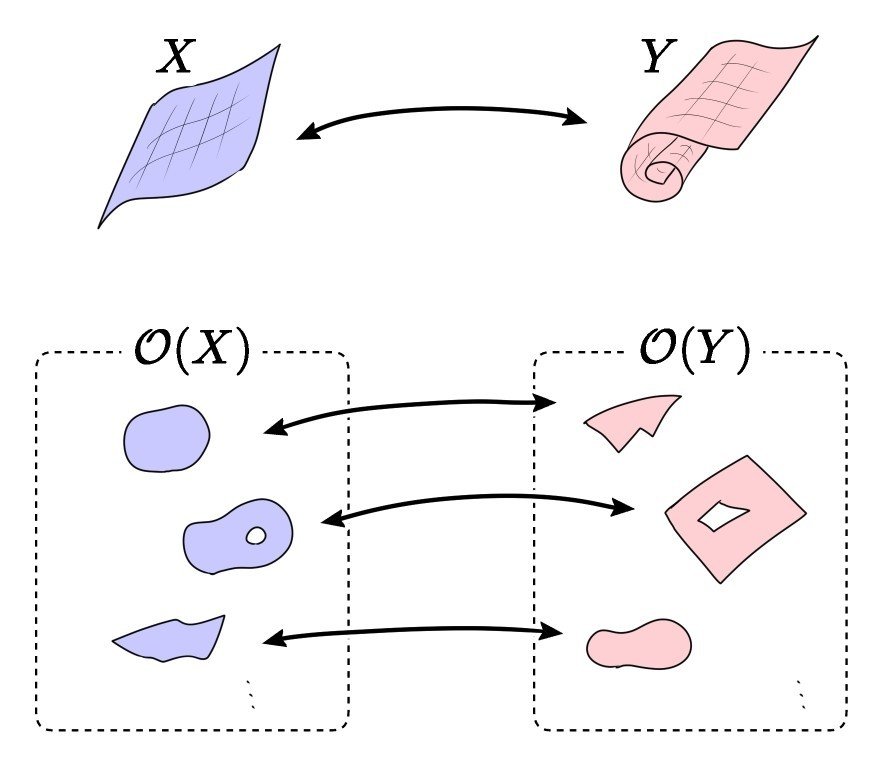
　ドーナッツとコーヒーカップが連続的に移り合う，というような説明を聞いたことがある人がいるかも知れません．

　この場合も，同相という考え方がされており，ドーナッツに定められた開集合と，コーヒーカップに定められた開集合が一対一に対応していることが，ドーナッツがコーヒーカップに変形できることとして説明されるのです．

　もう少し別な言い方をすると，ドーナッツ上で展開される連続理論と，コーヒーカップ上で展開される連続理論はまったく同じものになるというわけです．

　トポロジーという分野においては，このような簡単な図形だけではなく，もっと複雑な（高次元の）ものに対しての変形を定式化しなければいけなくなります．

　そんなときに位相空間の考え方は必要になってきます．

　また，位相空間は目に見える形の図形の変形を記述するのに有効なだけではなく，もっと抽象的なところでも活躍しています．

　代数幾何学という分野では，【ザリスキ位相】というユークリッド幾何で用いられるものとは違うものが使われています（上記の例において Oz(R) と書いたものはその一例です）．

　代数幾何学では，関数から空間を復元するという思想があります．すなわちある環 Y だけが最初に存在し，それを関数全体の環として持つような空間として 

Spec Y

というものが定義されます．これは Y の素イデアルとよばれるものからなる集合であり，そしてこの Spec Y にしかるべき開集合の情報を与えることにより位相空間となります．

　例えば，整数全体 Z も環であり，この Z を関数として持つような空間 Spec Z が構成されます．あるいは多項式全体を関数として持つような空間なども構成することができ，そこに現れる空間は私たちが普段扱っている空間とは似ても似つかないようなものになっています．（代数曲線そのものが点に集約されているような空間が得られる）．

ーーーーーーーーーー　

　このように位相空間は，わたしたちが思い描く【幾何学】だけにとどまらず，いろんな分野における幾何的な部分の基礎を成すものになっているのです．

　難関分野ではありますが，ここを乗り越えることで，純粋数学における抽象的な考え方のほとんどは習得できるようになるはずです．