第1節　簡単な関数の例

　まずは次のような関数を考えてみましょう．

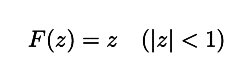
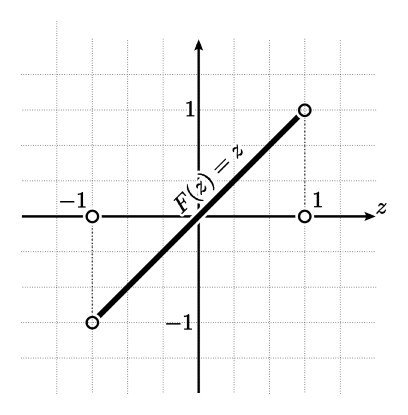
定義域に注意して下さい．この関数は |z| < 1 でしか定義されていません．この関数を実数全体に拡張したい場合どうすればよいでしょうか？

この場合は，単に定義域を【実数全体】に書き換えてしまえばいいだけで，何も難しいところはないように思われます．こうして実数全体に定義された関数を，F の上にニョロマーク ～ をつけて

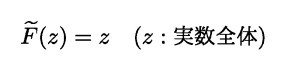
と書くことにします．この関数こそ，一部でしか定義されていなかった F(z) の，いわば【本体】であると言えます．

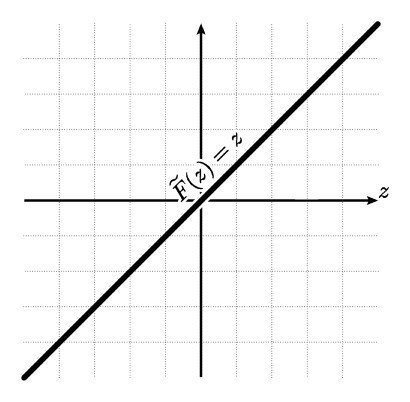
　以上の話は，定義域を書き換えるだけの話であり，関数の拡張に関する議論の重要性をあまり感じるものにはなっていません．

第2節　関数の式がおかしい？

　では，次の関数はどうでしょうか？

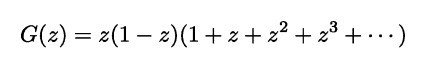
この関数は，数式中に現れる等比級数部分の収束を保証するために， | z | < 1 の範囲でしか定義されていないものです．それ以外の範囲では

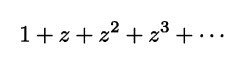
が発散してしまい，意味をなさなくなってしまいます．しかし，よくよく計算してみると， | z | < 1 の範囲で G ( z ) は次のように変形できます．

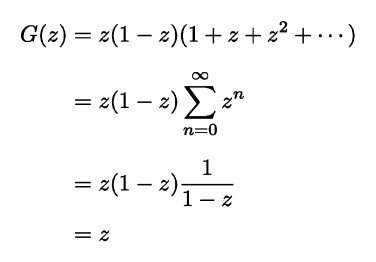
つまり， | z | < 1 の範囲において G(z) と F(z)= z ( | z | < 1 ) は，まったく同じ関数を表していることになります．それならば G(z) も F(z) と同じように

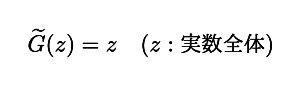
のように実数全体に拡張できるはずです．この関数が，一部でしか定義されていなかった G(z) の【本体】ということになります．ただし，ここで重要なことは， G(z) は最初の表示式のまま実数全体に拡張することはできないということです．

　仮に，拡張された関数

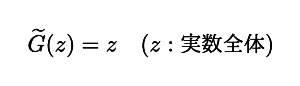
に z = 2 を代入したとすると

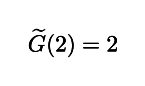
ですが，もともとの G(z) の表示式では

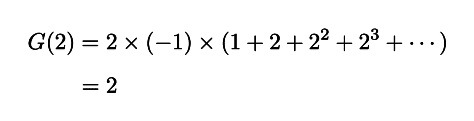
となってしまいます．これは意味のわからない式です． F(z) = z の場合は，もともとの関数に対して z = 2 を代入しても（数式的には）何も問題は起こりませんでした．

　つまり，

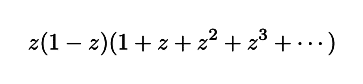
という数式は【本体の関数】を明示するのに十分な力を持っていないということになります．言い換えれば，本体の一部の情報しか持っていません．ただ，それでも【形式的な式変形】によって，

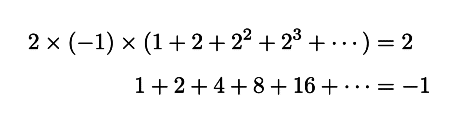
という式を導くことはできます（【形式的な式変形】というのは，式の持つ意味には一切着目せずに，記号的な操作のみで式変形を行うことを指す言葉です）．

第3節　ゼータ関数から得られる変な式

　以上と同様の話は，ゼータ関数にもあてはまります．ゼータ関数 ζ ( s ) は

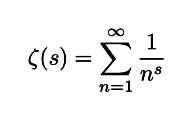
という級数によって与えられる関数です．ここで s という変数は複素数を動くものとしています．この級数が収束するために，関数の定義域は Re(s) > 1 ，つまり実部が 1 より大きい部分に制限されています．それ以外の点では数式が意味をなさなくなってしまうのです．

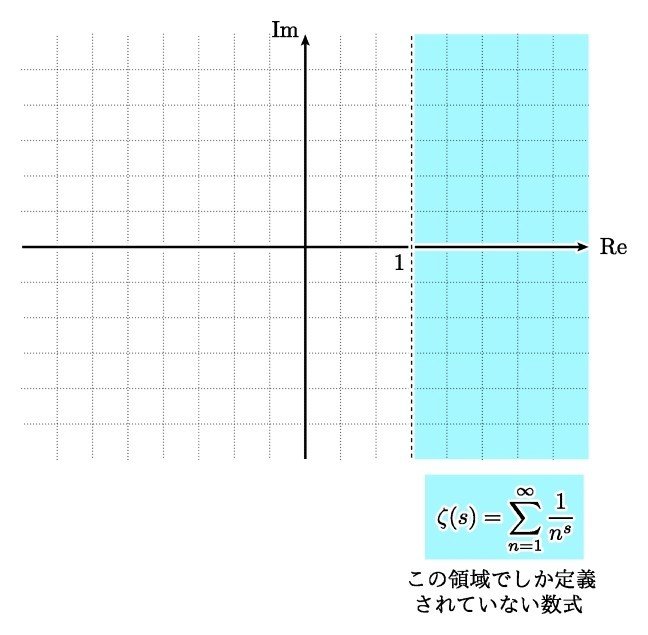
　しかし，さきほどの

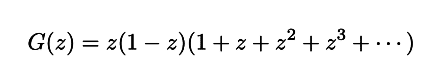
という関数が，別の表示式 G(z) = z ( |z| < 1 ) を得たことによって実数全体に拡張することができたように，ゼータ関数も別な表示式を得ることで，定義できる部分をもっと拡張できるかもしれません．

　一例を挙げてみましょう．ゼータ関数には次のような表示式も存在します．

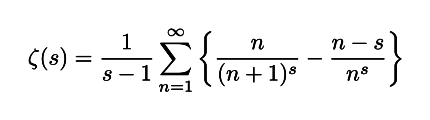
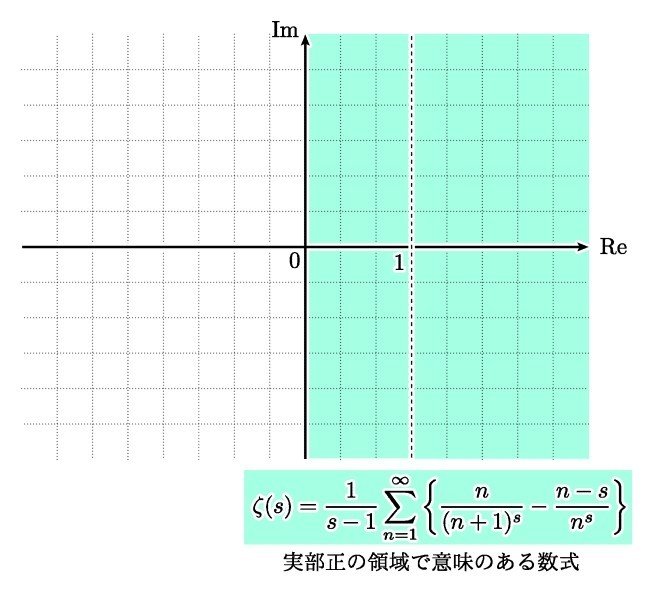
これは Re(s) > 0 の範囲で意味のある数式を与えており，なおかつ Re(s) > 1 の範囲でもともとの ζ(s) とも一致しています．

　よってこの数式により，ゼータ関数は実部が 0 より大きい範囲にまで定義域を拡張できたことになります．

　さらにゼータ関数は，実部負の領域にも拡張していくことができます．その方法は関数等式とよばれる以下の式

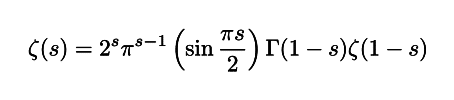
を用いるものです．この等式を使うことによって，すでに定義されている ζ(s) の部分を用いて，実部負の領域にまで拡張できます．

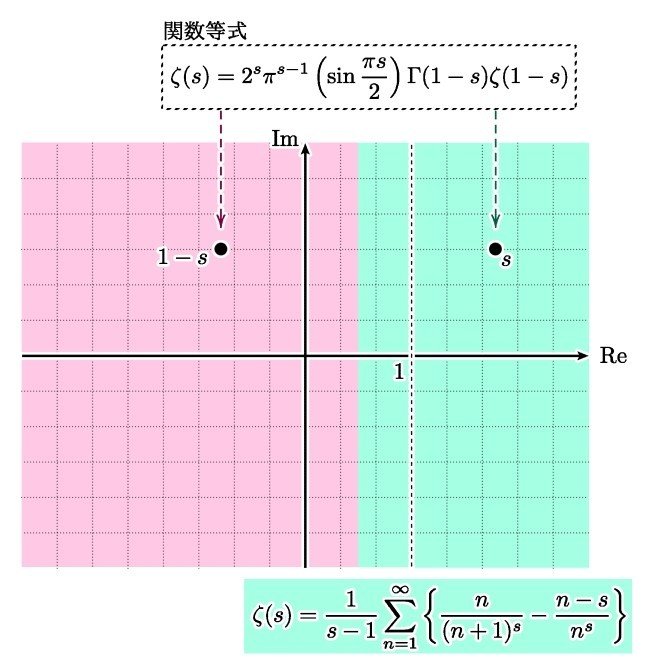
　結果的にゼータ関数 ζ(s) は上述のさまざまな表示式を用いて，複素平面全体に（一つの点を除いて）正則に拡張されます．【正則】とは複素微分可能という意味であり，【正則に拡張される】とは拡張後の関数が複素微分可能になるようにできることを意味します．

　さて，ゼータ関数が実部負の領域にも拡張されたということは，当然ゼータ関数に負の値を代入することによって意味のある値を得ることができます．拡張後のゼータ関数を

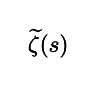
と書くことにしましょう．この関数に例えば，s = -1 を代入すると

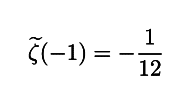
と計算できることが知られています．

　もともとのゼータ関数は，負の値では意味を成さなかったわけですが，むりやり負の値を ζ(s) に代入してしまえば，【形式的】に

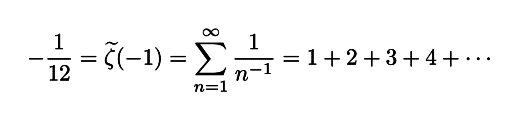
という式を得ることができます．

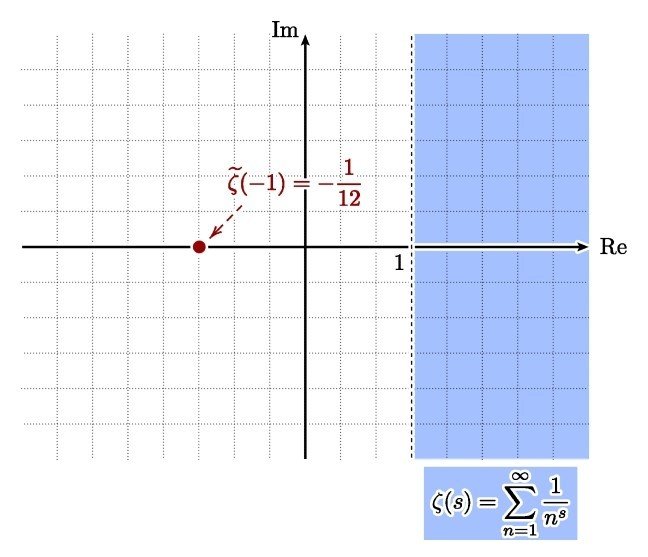
第4節　複素関数論からの補足【解析接続】

　最初に与えた関数 F(z) = z ( |z| < 1 ) に関して，これを実数全体に拡張すれば

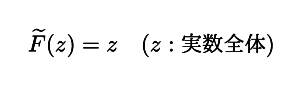
になると断言してしまっていますが，これは正確ではありません．

　この拡張の仕方はたしかに人間にとっては自然な拡張に見えますが，数学的に意味のある拡張が他にもあるかもしれません．その可能性は排除できていないのです．

　実際，F(z) を微分可能なまま拡張する方法はいくらでも存在します．

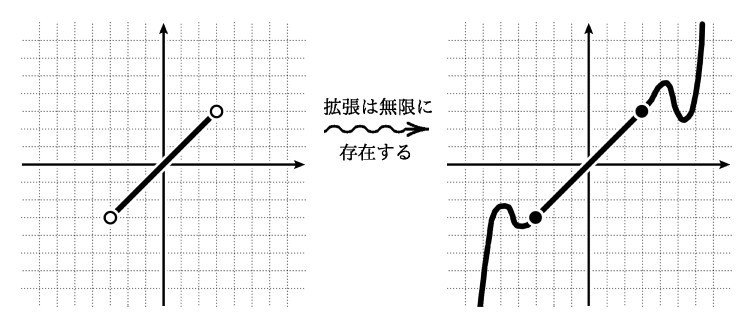
そのため F(z) を実数へ拡張しても，どれが真に本体の関数を与えてくれるのかはわからないのです．

　しかし複素関数となると話は違います．ある一部分でしか定義されていない複素関数は，正則な拡張が【たった一つしか存在しない】ことが証明されているのです．それは【一致の定理】とよばれています．

　----------【一致の定理】----------

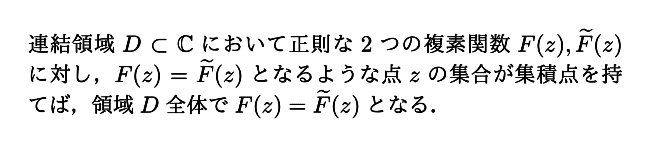
----------【一致の定理終】----------

　この定理によって，ゼータ関数はどんな式で表そうとも，正則でありさえすればその表示式が指し示す【本体の関数】はすべて同一のものになることが結論されるのです．このように，【たった一つの本体】に向かって定義領域を拡張していくことを【解析接続】とよんでいます．

　（ただし，細かい注意点があります．一致の定理は「もし拡張が存在すれば，それらは一致する」ということしか言っておらず，一般的には常に拡張が存在するとは限りません．簡単な例で言えば複素関数 f(z) = 1/z は z=0 に拡張できない関数です．）

第5節　まとめ

■ 数式が関数の情報をすべて持っているとは限らない

■ 拡張後の関数と，もともとの関数に値を代入したものをイコールでつなぐと【変な式】ができあがる

■ 1+2+3+...=-1/12 の左辺はもともとのゼータ関数の表示式，右辺は拡張後のゼータ関数に -1 を代入したもの

■ ある領域上（あるいは集積点を持つ集合上）で定義された複素関数の正則な拡張は，もし存在すれば一つしかない．これを【一致の定理】という．

■ 関数を正則に拡張していく方法を【解析接続】という