Pythonでやってみた(Engineering)：モンテカルロ法

2023年5月13日 22:34

１．概要

　モンテカルロ法（ランダム法, 多重確率シミュレーションとも呼ばれます）とは乱数を用いた数値シミュレーションとなります。乱数によりランダムな現象を作成して、将来的な動作を予測することが可能となります。
　概要として、”特定のコインの表が出る確率を調べる”場合、たくさんコイントスすることで確率が求められます。これをコンピューターにしてもらうようなものです。

　シミュレーションではありませんが、ランダム動作の参考例としてパックマンっぽい動きを実装しました。

[IN]
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import matplotlib.colors as colors
import random

# 迷路のサイズ
maze_size = (25, 25)

# パックマンの初期位置
pacman_position = [12, 12]

# 迷路の生成 (ランダムに壁を作り、外枠を壁にする)
maze = np.random.choice([0, 1], size=maze_size, p=[0.8, 0.2])
maze[0, :] = maze[-1, :] = maze[:, 0] = maze[:, -1] = 1

# パックマンの動き方を定義
moves = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 上、下、右、左

# カスタムカラーマップの作成
cmap = colors.ListedColormap(['white', 'saddlebrown'])

# 描画の準備
fig, ax = plt.subplots(figsize=(5, 5), facecolor='white')

# パックマンの位置を描画するための関数
def draw_pacman(position):
    ax.clear()
    ax.imshow(maze, cmap=cmap)  # 迷路を描画
    ax.scatter(*position, color='red')  # パックマンを描画
    ax.set(xlim=(-0.5, maze_size[1] - 0.5), ylim=(-0.5, maze_size[0] - 0.5))

# アニメーション更新関数
def update(i):
    # パックマンの次の位置をランダムに決定
    move = random.choice(moves)
    new_position = [pacman_position[0] + move[0], pacman_position[1] + move[1]]
    # 新しい位置が壁でなければ移動する
    if maze[new_position[1], new_position[0]] == 0:
        pacman_position[0], pacman_position[1] = new_position

    # パックマンの新しい位置を描画
    draw_pacman(pacman_position)

# アニメーションの生成
ani = animation.FuncAnimation(fig, update, frames=200, interval=200)

# GIFファイルとして保存
ani.save("pacman2.gif", writer='imagemagick')

[OUT]

１－１．名前の経緯

　カジノで有名な国家モナコ公国の4つの地区（カルティ）の1つであるモンテカルロから名付けられており、ギャンブルが名前の経緯となります。

１－２．応用事例

　モンテカルロ法の応用事例の一部として下記があります。

工学：人工システムのシミュレーション
自然科学：中性子拡散問題
金融工学：オプションの価格設定、株価シミュレーション
コンピューターグラフィックス：パストレーシング
機械学習：バンディット問題
物理科学：軌道追跡モンテカルロシミュレーション

２．基礎知識・用語

　まずは押さえておきたい用語を紹介します。

２－１．モンテカルロステップ：MCS

　モンテカルロ法では乱数を引きシミュレーションします。乱数を引いた数（より詳細には乱数を引いて処理するまでの一連のフロー）をモンテカルロステップ：Monte Carlo Sweep(MCS)と言います。

３．モンテカルロシミュレーション

３－１．数値積分

　モンテカルロ法により円周率$${\pi}$$を求めます。シミュレーションフローは下記の通りです。

単位正方形（辺の長さが1の正方形）内に単位円（半径1の円）を描写
正方形内にランダムに点を打つ
打った点のうち、円の内部（$${x^2 + y^2 \leq 1}$$）の点をカウント
全体の点に対する円内の点の割合を計算
は正方形の面積に対する円の面積の割合($${\frac{\pi}{4}}$$)に近似されるため下記式で円周率$${\pi}$$)

$$
\pi \approx 4 \times \frac{\text{円の内部にある点の数}}{\text{全体の点の数}}
$$

　フローを可視化するコードは下記の通りです。

[IN]
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# モンテカルロ法で円周率を求めるための設定
N = 1000 # 点を打つ回数
x = np.random.rand(N)
y = np.random.rand(N)
inside = x**2 + y**2 <= 1 # 円の内側に点があるかどうか.r^2 = x^2 + y^2
print(f'データ形状 X: {x.shape}, Y: {y.shape}, inside: {inside.shape}')
print('X：', x[:10])
print('Y：', y[:10])
print('inside：', inside[:10])

fig, ax = plt.subplots(figsize=(10, 10), facecolor='white')
scatter, = ax.plot([], [], 'o', markersize=5)
text = ax.text(0.5, 1.05, '', transform=ax.transAxes, ha='center')
text.set_fontsize(20)  # フォントサイズを15に設定
ax.fill_between(np.linspace(0, 1, 100), 0, np.sqrt(1-np.linspace(0, 1, 100)**2), color='lightcoral', alpha=0.3)

# アニメーションの初期化
def init():
    ax.set_xlim(0, 1)
    ax.set_ylim(0, 1)
    ax.set_xticks(np.linspace(0, 1, 11))
    ax.set_yticks(np.linspace(0, 1, 11))
    scatter.set_data([], [])
    text.set_text('')
    return scatter, text

# アニメーションの更新
def update(frame):
    scatter.set_data(x[:frame], y[:frame])  # データ点の数を確定
    pi = 4 * np.sum(inside[:frame]) / frame
    text.set_text(r'データ数(In):{:d} データ数(Out):{:d} $\pi$={:.3f}'.format(frame, frame-np.sum(inside[:frame]), pi))
    return scatter, text

ani = animation.FuncAnimation(fig, update, frames=range(1, N+1, 2), init_func=init, blit=True)
ani.save('monte_carlo.gif', writer='pillow', fps=10)
plt.show()

[OUT]
データ形状 X: (1000,), Y: (1000,), inside: (1000,)

X： [0.24942003 0.09346238 0.64067246 0.15673021 0.33128532 0.35610397
 0.57214957 0.95714866 0.60702108 0.97412966]
Y： [0.52137912 0.72674023 0.34638678 0.4554468  0.73446368 0.48168354
 0.65660826 0.18330699 0.04632439 0.35314262]
inside： [ True  True  True  True  True  True  True  True  True False]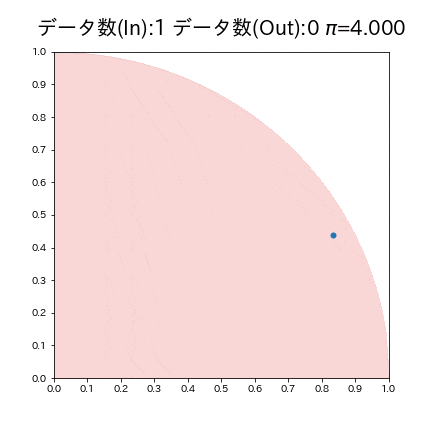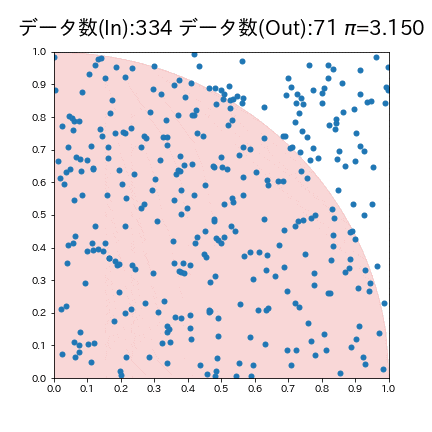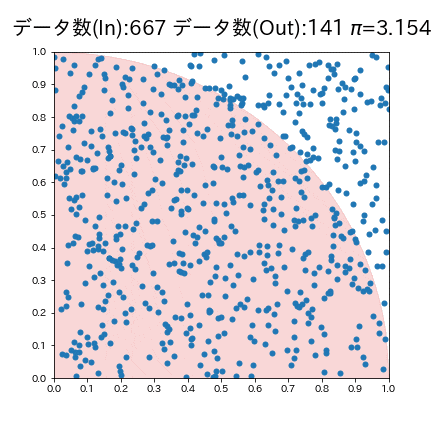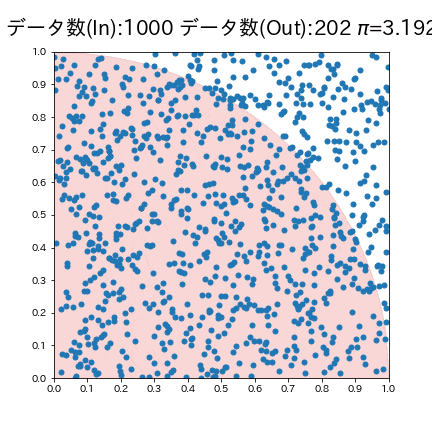

　別パターンでの可視化も実施しました。試行回数を重ねることで理論値に値数いていることが確認できます。

[IN]
#insideのTrue=1, False=0に変換して累積和を取る
inside_binary = np.array(inside, dtype=int) # True=1, False=0に変換
_ratio = np.cumsum(inside_binary) / np.arange(1, N+1) # 累積和を取る
ratio = 4 * _ratio # 円周率の近似値
#可視化
fig, ax = plt.subplots(figsize=(6, 4), facecolor='white')
ax.plot(ratio, color='blue', label='モンテカルロ法')
ax.hlines(np.pi, 0, N, color='red', linestyle='--', label='真の円周率')
ax.set(xlabel='試行回数', ylabel=r'円周率の近似値$4\times \frac{円内の点}{全点数}$', xlim=(0, N), ylim=(2.0, 4.0), xticks=np.linspace(0, N, 11))
ax.grid(), ax.legend()
plt.show()

[OUT]

３－２．将来株価のシミュレーション

　モンテカルロ法により将来の株価をシミュレーションしてみます。あくまで株価が時間と共にランダムで動くことを想定しているだけなので、実際の株に適用は難しいですが理論の理解には役立ちます。

　数式は上記記事を参照しました。

【ブラウン運動（またはウィーナー過程）】
　気体や液体の分子は、たえず熱運動をしています。そして気体中や液体中にある微粒子も、これらいくつかの分子に衝突され続けています。その結果、微粒子は不規則に動かされることになります。このような微粒子の運動を「ブラウン運動」といいます。

　一方で金融工学におけるブラウン運動（特に幾何ブラウン運動）は、金融商品の価格変動を表すための数学的モデルです。このブラウン運動は時間に対して連続的な確率過程で特に株価などの資産価格の動きをモデル化するために用いられます（物理学のブラウン運動とは式が異なる）。

$$
W_t = \sum \sqrt{\Delta t} Z
$$

$${W_t}$$ ：時間 t におけるブラウン運動の値
$${\Delta t}$$：時間ステップ
$${Z}$$：標準正規分布に従うランダム変数

【幾何ブラウン運動】
　ブラウン運動を拡張した幾何ブラウン運動は金融商品の価格変動などのモデル化に使用されます。下記のような形を幾何ブラウン運動(geometric Brownian Motion)といいます。

$$
S_t = S_0 \exp \left( \left(\mu - \frac{1}{2}\sigma^2 \right) t + \sigma W_t \right)
$$

$${S_t}$$ ：時間 t での株価
$${S_0}$$：初期の株価
$${\mu}$$：無リスク短期金利
$${\sigma}$$：株価のボラティリティ（変動の大きさを表す）
$${W_t}$$：標準ブラウン運動

　今回のシミュレーションでは株価100円の株が1年後にいくらになるかを想定するため、1年を100分割(ステップ数）にして、1万回シミュレーションしました（１万個の株価変動パターンを作成）。
　シミュレーションのうち１０個を抽出してどのような動きになるか可視化しました。結果として様々な株価変動パターンが得られました。

[IN]
import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
S0 = 100  # 初期株価
T = 1.0  # 時間期間（年）
r_interest = 0.05  # 無リスク短期金利
sigma = 0.2  # ボラティリティ（株価の変動の大きさを表す）
M = 100  # 時間ステップ数
dt = T / M  # 一ステップあたりの時間
I = 10000  # シミュレーション回数

# モンテカルロシミュレーション
np.random.seed(0)
W = np.cumsum(np.sqrt(dt) * np.random.standard_normal((M + 1, I)), axis=0)  # ブラウン運動
print(W.shape)
S = S0 * np.exp((r_interest - 0.5 * sigma ** 2) * dt * np.arange(M + 1)[:, np.newaxis] + sigma * W)  # 幾何ブラウン運動モデル
print(S.shape)


# シミュレーション結果の可視化（最初の10パスだけ表示）
fig, axs = plt.subplots(2, 1, figsize=(16, 10), facecolor='white')
ax1, ax2 = axs[0], axs[1]

#ブラウン運動
ax1.plot(W[:, :10], lw=1.5)
ax1.set(xlabel='time step', ylabel='index level', title='ブラウン運動', xticks=np.linspace(0, 100, 11))

#幾何ブラウン運動モデル
ax2.plot(S[:, :10], lw=1.5)
ax2.set(xlabel='time step', ylabel='index level', title='株価シミュレーション（幾何ブラウン運動モデル）', xticks=np.linspace(0, 100, 11))

ax1.grid(True), ax2.grid(True)
plt.show()



[OUT]
(101, 10000)
(101, 10000)

参考記事

あとがき

　次はマルコフ連鎖モンテカルロ法（MCMC: Markov Chain Monte Carlo）

この記事が気に入ったらサポートをしてみませんか？