次回、回帰直線を用いた記事が書きたいため、今回は回帰直線についてお話ししようと思います。

2変数関数の最小値を求める際に偏微分を用いる解説が多いのですが、今回は少し複雑になってしまいますが数Iの2次関数を利用して求めるため、必要な知識は数Iまでとなっています。

必要な知識

二次関数の最小値

$${x,y}$$は実数とする。

例えば、

$$
f(x,y) = x^2 + y^2 + 1
$$

は$${x=0, y=0}$$のとき、$${f(x,y)}$$の最小値は1である。

$$
f(x,y) = (x-y)^2 + (y-2)^2 + 2
$$

の場合だと、

$$
x-y = 0, y-2 = 0
$$

すなわち、

$$
x = 2, y = 2
$$

のとき、$${f(x,y)}$$の最小値2をとる。

最後に以下の例を見てみる。

$$
f(x,y) = 2x^2 + y^2 - 2xy + 4x - y + 1
$$

上の例でやったような形にすれば最小値が分かる。これは平方完成をすることにより上のような形になる。

$$
\begin{split}
f(x,y) &= 2x^2 + y^2 - 2xy + 4x - y + 1 \\
&= 2x^2 - 2(y - 2)x + y^2 - y + 1 \\
&= 2\left(x - \frac{y-2}{2}\right)^2 + \frac{y^2 + 2y - 2}{2} \\
&= 2\left(x - \frac{y-2}{2}\right)^2 + \frac{1}{2}(y + 1)^2 - \frac{3}{2}
\end{split}
$$

となるので、

$$
x - \frac{y-2}{2} = 0, y+1 = 0
$$

すなわち、

$$
x = -\frac{3}{2}, y = -1
$$

のとき、$${f(x,y)}$$の最小値は$${-\frac{3}{2}}$$となる。

Σの基本性質

$$
x_1 + x_2 + \cdots + x_n
$$

といった式がたくさん出てきて、式が冗長になってしまうためΣを使って、

$$
\sum_{i=1}^nx_i
$$

と表す。

この記事では、

$$
\sum_{i=1}^n(x_i + y_i) = \sum_{i=1}^nx_i + \sum_{i=1}^ny_i
$$

と

$$
\sum_{i=1}^ncx_i = c\sum_{i=1}^nx_i
$$

だけ抑えておけば十分である。

また、今回は

$$
\sum_{i=1}^nx_i^2 = x_1^2 + x_2^2 + \cdots + x_n^2
$$

と

$$
\left(\sum_{i=1}^nx_i\right)^2 = (x_1 + x_2 + \cdots + x_n)^2
$$

がたくさん出てきるため、この2つの違いに注意する。

平均と分散と共分散

• 平均

データ$${x_1,x_2,\cdots, x_n}$$に対して、平均$${\bar{x}}$$は

$$
\bar{x} = \frac{x_1 + x_2 + \cdots + x_n}{n} = \frac{1}{n}\sum_{i=1}^nx_i
$$

と表す。

• 分散

データ$${x_1,x_2,\cdots, x_n}$$に対して、分散$${\sigma_x^2}$$は

$$
\begin{split}
\sigma_x^2 &= \frac{1}{n}\left\{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2\right\} \\
&= \frac{1}{n}\sum_{i=1}^n(x_i - \bar{x})^2
\end{split}
$$

また、$${\sigma_x^2}$$は

$$
\sigma_x^2 = \frac{1}{n}\sum_{i=1}^nx_i^2 - \left(\frac{1}{n}\sum_{i=1}^nx_i\right)^2
$$

と変形できる。

• 共分散

データ$${(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$$に対して、共分散$${\sigma_{xy}}$$は

$$
\begin{split}
\sigma_{xy} &= \frac{1}{n}\left\{(x_1 - \bar{x})(y_1 - \bar{y}) + (x_2 - \bar{x})(y_2 - \bar{y}) + \cdots + (x_n - \bar{x})(y_n - \bar{y})\right\} \\
&= \frac{1}{n}\sum_{i=1}^n(x_i - \bar{x})(y_i - \bar{y})
\end{split}
$$

また、$${\sigma_{xy}}$$は

$$
\sigma_{xy} = \frac{1}{n}\sum_{i=1}^nx_iy_i - \left(\frac{1}{n}\sum_{i=1}^nx_i\right)\left(\frac{1}{n}\sum_{i=1}^ny_i\right)
$$

と変形できる。

回帰直線と最小二乗法

回帰分析

2変数$${x,y}$$のデータに対し、説明する変数「説明変数」$${x}$$が説明される変数「被説明変数」$${y}$$にどのような影響を及ぼすかを回帰方程式と呼ばれる式を用いて分析する統計手法。

回帰直線

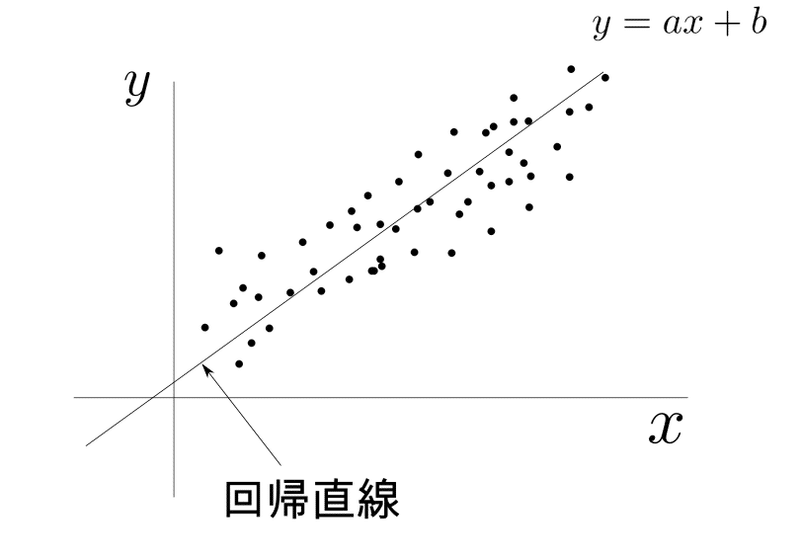
1次関数

$$
y = ax + b
$$

で表される回帰方程式を回帰直線という。

最小二乗法

回帰直線を推定する手法

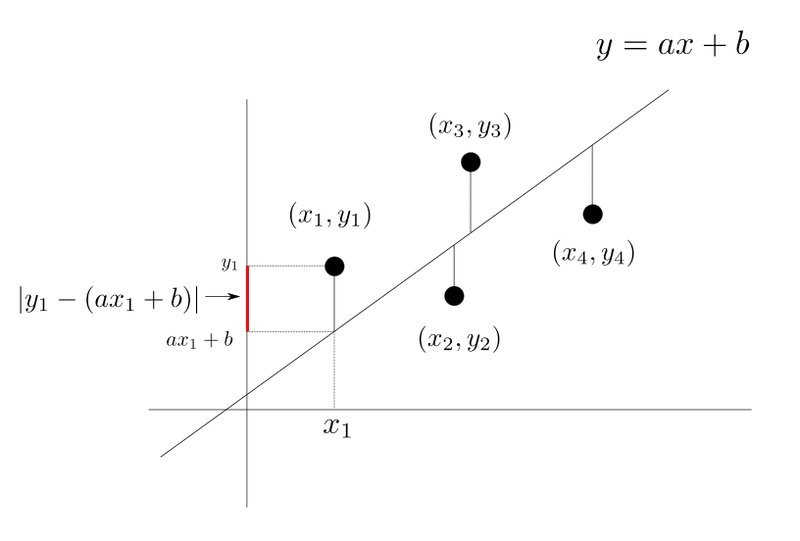
各点$${(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$$に対して、距離

$$
|y_i-(ax_i + b)|
$$

の和が最小となるように$${a,b}$$を求め、回帰直線を導き出す。しかし、絶対値だと計算が困難なため、

$$
\sum_{i=1}^n{y_i-(ax_i + b)}^2
$$

が最小となるように直線

$$
y = ax + b
$$

を導き出す手法が最小二乗法である。

最小二乗法により回帰直線を求める

$$
L = \sum_{i=1}^n{y_i-(ax_i + b)}^2
$$

が最小となる$${a,b}$$を求める。

$$
\begin{split}
L &= \sum_{i=1}^n{y_i-(ax_i + b)}^2 \\
&=\sum_{i=1}^n(b^2 - 2(y_i - x_ia)b + y_i^2 - 2x_iy_ia + x_i^2a^2) \\
&= nb^2 - 2\sum_{i=1}^n(y_i-x_ia)b + \sum_{i=1}^n (y_i^2 - 2x_iy_ia + x_i^2a^2) \\
&= n\left(b-\frac{\displaystyle\sum_{i=1}^n(y_i-x_ia)}{n}\right)^2 + \frac{n\displaystyle\sum_{i=1}^n(y_i^2 - 2x_iy_ia + x_i^2a^2)-\left(\sum_{i=1}^n(y_i-x_ia)\right)^2}{n}
\end{split}
$$

ここで、

$$
F(a) = n\displaystyle\sum_{i=1}^n(y_i^2 - 2x_iy_ia + x_i^2a^2)-\left(\sum_{i=1}^n(y_i-x_ia)\right)^2
$$

について整理すると、

$$
\begin{split}
F(a) &= n\displaystyle\sum_{i=1}^n(y_i^2 - 2x_iy_ia + x_i^2a^2)-\left(\sum_{i=1}^n(y_i-x_ia)\right)^2 \\
&= n\displaystyle\sum_{i=1}^n(y_i^2 - 2x_iy_ia + x_i^2a^2)-\left(\left(\sum_{i=1}^ny_i\right)^2-2\left(\sum_{i=1}^nx_i\sum_{i=1}^ny_i\right)a + \left(\sum_{i=1}^nx_i\right)^2a^2\right) \\
&= \left(n\sum_{i=1}^n x_i^2 - \left(\sum_{i=1}^nx_i\right)^2\right)a^2 - 2\left(n\sum_{i=1}^nx_iy_i-\sum_{i=1}^nx_i\sum_{i=1}^ny_i\right)a + n\sum_{i=1}^n y_i^2 - \left(\sum_{i=1}^ny_i\right)^2 \\
&= \left(n\sum_{i=1}^n x_i^2 - \left(\sum_{i=1}^nx_i\right)^2\right)\left(a-\frac{n\displaystyle\sum_{i=1}^nx_iy_i-\sum_{i=1}^nx_i\sum_{i=1}^ny_i}{n\displaystyle\sum_{i=1}^n x_i^2 - \left(\sum_{i=1}^nx_i\right)^2}\right)^2 + (x_iとy_iの式)
\end{split}
$$

となる。よって、

$$
a = \frac{\displaystyle n\sum_{i=1}^nx_iy_i-\sum_{i=1}^nx_i\sum_{i=1}^ny_i}{\displaystyle n\sum_{i=1}^nx_i^2-\left(\sum_{i=1}^nx_i\right)^2},
$$

$$
\begin{split}
b &= \frac{\displaystyle\sum_{i=1}^n(y_i-x_ia)}{n} \\
&= \frac{\displaystyle \sum_{i=1}^nx_i^2\sum_{i=1}^ny_i-\sum_{i=1}^nx_iy_i\sum_{i=1}^nx_i}{\displaystyle n\sum_{i=1}^nx_i^2-\left(\sum_{i=1}^nx_i\right)^2}
\end{split}
$$

のとき、$${L}$$は最小値をとる。

平均、分散、共分散との関係

データ$${(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$$に対して、$${x_1,x_2, \cdots , x_n}$$の分散を$${\sigma_x^2}$$,$${(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$$の共分散を$${\sigma_{xy}}$$とすると、

$$
n^2\sigma_x^2 = n\sum_{i=1}^nx_i^2 - \left(\sum_{i=1}^nx_i\right)^2
$$

$$
n^2\sigma_{xy} = n\sum_{i=1}^nx_iy_i - \sum_{i=1}^nx_i\sum_{i=1}^ny_i
$$

より、

$$
a = \frac{\sigma_{xy}}{\sigma_{x}^2}
$$

また、

$$
b = \frac{\displaystyle\sum_{i=1}^n(y_i-x_ia)}{n}
$$

より、

$$
b = \bar{y} - a\bar{x}
$$

となる。

まとめ

データ$${(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$$に対して、最小二乗法による回帰直線を

$$
y = ax + b
$$

とすると、

$$
a = \frac{\displaystyle n\sum_{i=1}^nx_iy_i-\sum_{i=1}^nx_i\sum_{i=1}^ny_i}{\displaystyle n\sum_{i=1}^nx_i^2-\left(\sum_{i=1}^nx_i\right)^2},
$$

$$
b = \frac{\displaystyle \sum_{i=1}^nx_i^2\sum_{i=1}^ny_i-\sum_{i=1}^nx_iy_i\sum_{i=1}^nx_i}{\displaystyle n\sum_{i=1}^nx_i^2-\left(\sum_{i=1}^nx_i\right)^2}
$$

となる。

また、$${x_1,x_2, \cdots , x_n}$$の分散を$${\sigma_x^2}$$, $${(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$$の共分散を$${\sigma_{xy}}$$とすると、

$$
a = \frac{\sigma_{xy}}{\sigma_{x}^2},
$$

$$
b = \bar{y} - a\bar{x}
$$

となる。

最後まで読んでくださりありがとうございます。

少しでもコメの記事が面白そうだなーと思ってくれた方はフォローやスキをお願いいたします。