高校以来、数学とか全然触れる機会のなかった初心者のコーダーが、「ベクトルの外積が平行四辺形の面積になる」とか、「CCW（counter clockwise、反時計周り）のアルゴリズム」とからへんの話が全然わからなかったので、自分で調べて『初心者はこれだけ知っていれば足りるくね』と思ったことを、書いておきます。

たぶんですけど、ちゃんと数学に詳しい人が書くより、読みやすくてわかりやすいと思います。突っ込んだことはわかんないけどね！
（ググってもちゃんとした難しめの説明しか出てこなくて困ったんですよ・・・）

あ、あと2Dのベクトルの話です、って先に書いておいた方がいいのかな（3Dのベクトルとかわからん）。

1、反時計周りのアルゴリズムに、ベクトルの外積を利用する。

「ベクトルの外積とはいったい何なのか」はとりあえず一旦置いておくとして、まずはCCW(counter clockwise)、すなわち反時計周りのアルゴリズムの話から始めましょう。

CCWのアルゴリズムとは、二つの交わる直線があるとき、「その二つの直線が反時計回りを描いているか、一直線になっているか、時計回りを描いているのか」を判定するのに使われるアルゴリズムです。
そのCCWのアルゴリズムに、ベクトルの外積というものを使う、というわけです。

あ、せっかちさんのために、先にCCW関数のサンプルだけ置いておきます。

// 頂点P,Q,Rの座標を引数にとり、直線PQ、QRが反時計回りであるかを判定する
int CCW(pair <int, int> P, pair <int, int> Q, pair <int, int> R){

    //ベクトルPQ、QRの成分を計算する
    pair<int, int> vector_PQ = make_pair(Q.first - P.first, Q.second - P.second);
    pair<int, int> vector_QR = make_pair(R.first - Q.first, R.second - Q.second);

    // ベクトルPQ、QRの外積を計算する。
    // ベクトルA(ax, ay)とベクトルB(bx, by)の外積は「ax * by - ay * bx」
    int area = vector_PQ.first * vector_QR.second - vector_PQ.second * vector_QR.first;

    // CCWの判定。
    // 直線PQ、QRが反時計回りであるときは1を、時計回りであるときは-1を、
    // 一直線に並ぶときは0を返す
    if (area > 0) {
        return 1;
    }
    else if (area < 0){
        return -1;
    }    
    else{
        return 0;
    }
}

はい、ではここから解説です。

最初にちょっとだけベクトルの定義に触れておくことにしましょう。
ベクトルとは、向きと大きさで決まる量のことで、位置は無視してかまいません。
逆に言えば任意の位置に動かして考えてもベクトルを使った計算自体としては全く同じということです。

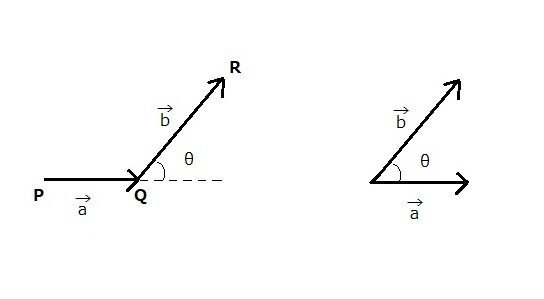
時計周り・反時計回りを判定するのは、左図のように頂点の位置関係が問題になってくる場面だと思います。
一方の右図はベクトルaとベクトルｂの始点が同じになるよう動かして、両者を見比べられるように並べました。
外積の計算では、ベクトルaとベクトルbの成す角度θというのが出てくるのですが、そのθの位置が左図においてはどこになるかということを、頭にいれておいてくださいね。

それでは外積の公式を見てみましょう。公式といっても、簡単ですから大丈夫ですよ。

大事なのは、外積を求める公式は二つあり（細かい式変形や証明は数学に詳しい人に任せるとして）、この二つの式の計算結果は同じ値になるということです。

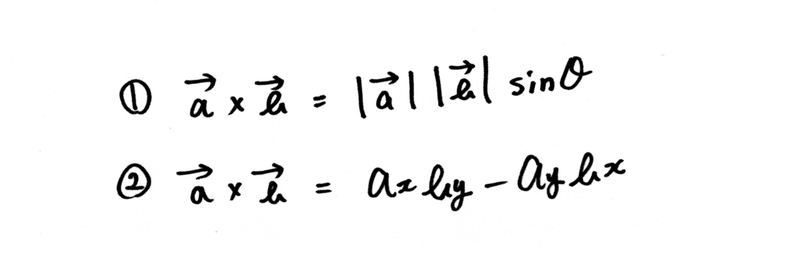
（手書きですみませんね、ベクトルをキーボード入力できないもので）

①は二つの線分の大きさ（絶対値で挟まれたベクトル）と三角関数（sinθ）を使った計算方法であるのに対し、
②はベクトルの成分（ベクトルの始点を仮に原点としたとき、終点となる座標）を使った計算方法になります。

たとえば「今θ=71°なので、①の式で外積を計算してください」と言われたら「sin71°なんてどうやって求めるんだよ！」と発狂しますが、②の式の場合は座標の値を機械的に代入すれば求められるので計算は楽チンですね。

CCW判定は、この二つの式の計算結果が同じになることを利用します。
つまり計算の簡単な②の式で計算を行い、その計算結果が①の式の答えと等しくなることを利用するのです。
もっといえば、計算結果の値は別にどうでもよくて、計算結果の符号だけを見ていればCCW判定は事足ります。

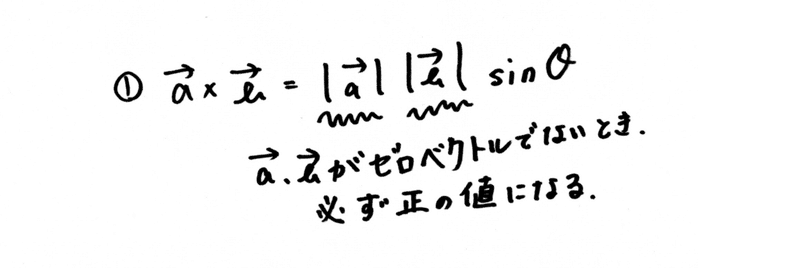
ここで注目して欲しいのは、①の公式において絶対値で挟まれたベクトル、つまり線分の大きさというのは、(ゼロベクトルでない限り)必ず正の値になる、ということです。と、いうことは・・・？

sinθの値の範囲は、-1 <= sinθ <= 1であるので、

・外積が正であるとき、sinθの値は0 < sinθ <= 1、すなわち0° < θ < 180°
・外積が0であるとき、sinθの値はsinθ = 0、すなわちθ = 0° か、θ = 180°
・外積が負であるとき、sinθの値は-1 <= sinθ < 0、すなわち180° < θ < 360°

となります。
ここまで来たら、最初の図に戻って、θがどの角度を示していたかを考えれば、CCWのアルゴリズムは理解できるはずです。

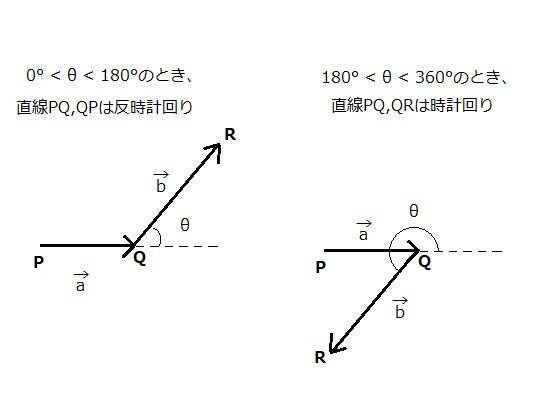
以上が（たぶん）最低限のCCWの説明になります。
面積の話をすっとばしても、反時計回り判定自体は理解できますね。

2、外積が平行四辺形の『符号付き面積』になるとはどういうことか。

ここからはもう少し外積の公式①の意味を、図形的に理解していきましょう。
注目するのはこの下線部分です。

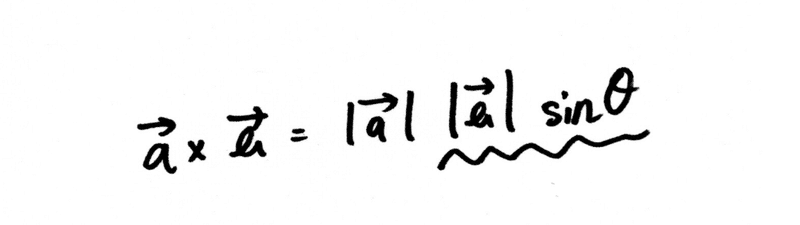
実は、この下線を引いた「ベクトルbの大きさ」とsinθを掛けた値というのは、図形で表すと下左図のオレンジの部分、すなわちベクトルbの終点からベクトルaの延長線上におろした垂線の長さになります。

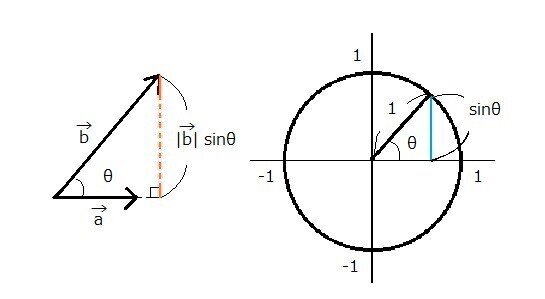
右の図は三角関数とか忘れた、という人のために一応書いておきました。
三角関数を習うときによく見るやつで、sinθの値がどこを意味しているかを示したものです。
右図において、斜辺の長さが1のときの青線の長さがsinθであるから、
左図においてオレンジ線の長さがベクトルbの大きさとsinθの値を掛けたものになるのはわかりますよね。

ここで平行四辺形の面積の求め方を思い出してみましょう。

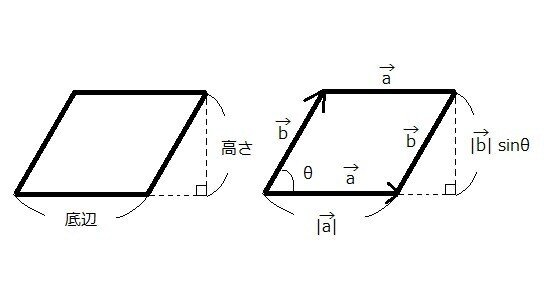
あ！
平行四辺形の面積を求める「底辺×高さ」を右図で行うと、外積を求める公式①と一致します。
ということは、ベクトルの外積は、平行四辺形の面積を表すんだ！

また180° < θ < 360°であるときは、

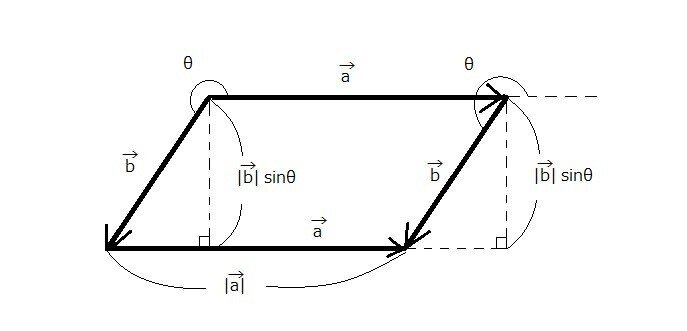
ここの面積をあらわしていることになるんでしょう。ほとんど同じですが、ベクトルbの向きが変わっています。
このときのsinθはマイナスになるので、外積すなわち符号付き面積でいえばマイナスの値になります。
面積にマイナスの符号が付くなんて不思議ですが、なんかそういうもんらしいです。

と、私が理解したのはここまでで、ここから先の話も少しばかり読み進んでみましたがなんか意味わからん方向に進んでいくので、正直さっぱりです。

私のような初心者コーダーは、これだけわかっていれば十分でしょう。

3，おまけ　～ベクトルの内積～

せっかくですのでベクトルの内積についても、覚え書きしておきます。

まずは表記の仕方。

外積には「×」の演算子を使い、内積には「・」の演算子を使うことで区別するようです。

そして内積の求め方です。
内積を求める公式も外積と同じく、二つあるようです。

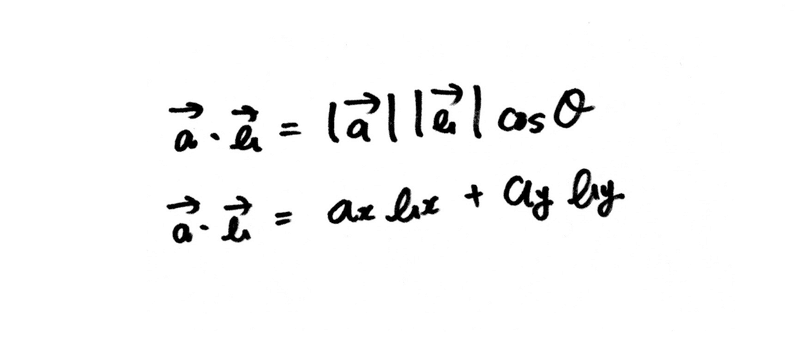
外積ではsinθだったところが、内積ではcosθに変わります。
また、成分の掛け方も変わりますね。

そして外積の時と同じように、「ベクトルbの大きさ」とcosθを掛けたものが図形的にどこにあたるかを見てみると、下の図のようになります。

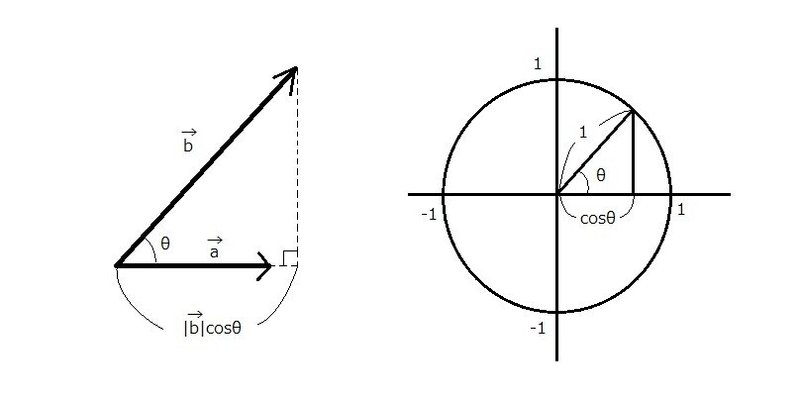
内積はこことベクトルaの大きさを掛け合わしたものになるのですが、こうみると内積というものが図形的に何を意味しているのかは、いまいちよくわからないですね・・・。
こう考えるとベクトルの内積より、図形的には外積の方が理解しやすい気がします・・・。

というわけで、この記事は以上で終わりです。
私のように数学にそんなに詳しくない人でも、ベクトルやCCW判定を理解するための足掛かりになれば幸いです。

それでは。