単回帰モデル、および推定量について勉強したのでメモ
時間が余った時に例題追加予定…

結論

$$
\begin{align*}
\hat{\alpha} &= \overline{y} - \frac{ \sigma_{xy} }{\sigma_x^2}\overline{x} \\
\hat{\beta} &= \frac{ \sigma_{xy} }{\sigma_x^2} \\
\hat{\sigma}^2 &= \frac{n}{n-2}\sigma^2_y\left(1 - r_{xy}^2\right) \\
\hat{\alpha} &\sim N\left(\alpha, \frac{\hat{\sigma}^2}{n}\left(1+\frac{\overline{x}^2}{\sigma^{2}_{x}}\right)\right)\\
\hat{\beta} &\sim N\left(\beta,  \frac{1}{n}\frac{\hat{\sigma}^2}{\sigma_{x}^{2}}\right)\\
\end{align*}
$$

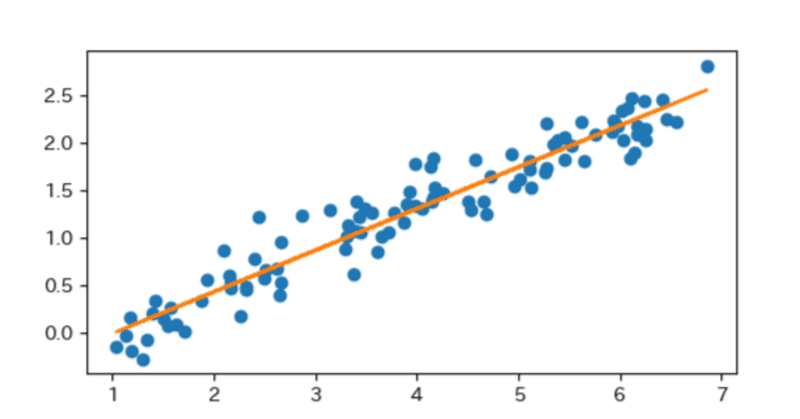
単回帰モデルの定義

単一の説明変数$${x}$$を用いて目的変数$${y}$$の関係を統計的に捉える手法のこと
パラメータ$${\alpha, \beta}$$と誤差項$${\epsilon}$$を用いて下記のようにあらわされる

$$
\begin{align*}
y = \alpha + \beta x + \epsilon
\end{align*}
$$

単回帰モデルの前提条件

【前提1】
$${i}$$番目の観測値$${x_i, y_i}$$とパラメータ$${\alpha, \beta}$$、誤差項$${\epsilon_i}$$を用いて次の方程式で表される

$$
\begin{align}
y_{i} = \alpha + \beta x_{i} + \epsilon_{i}
\end{align}
$$

【前提2】
誤差項$${\epsilon_i}$$は互いに独立で同一の平均0の正規分布に従う

$$
\begin{gather*}
\epsilon_{i} \sim N(0, \sigma^2) \\
f_{\epsilon_i, \epsilon_j}(\epsilon_i = a, \epsilon_j=b) = f_{\epsilon_i}(\epsilon_i=a)f_{\epsilon_j}(\epsilon_j=b)    (i \neq j)
\end{gather*}
$$

最小二乗法によるパラメータ推定

$${n}$$個のデータが存在するときの誤差項の平方和$${\sum^{n}_{i=1}\epsilon_i^2}$$が最小となる$${\alpha, \beta}$$の組み合わせを見つけ推定量$${\hat{\alpha},\hat{ \beta}}$$とする
$${(1)}$$を式変形する

$$
\begin{align*}
\epsilon_{i} &= y_{i} - \alpha - \beta x_{i} \\
\epsilon_{i}^2 &= (y_{i} - \alpha - \beta x_{i})^2 \\
\sum^{n}_{i=1}\epsilon_i^2 &= \sum^{n}_{i=1}(y_{i} - \alpha - \beta x_{i})^2
\end{align*}
$$

$${\sum^{n}_{i=1}(y_{i} - \alpha - \beta x_{i})^2}$$を最小とする$${\alpha, \beta}$$を見つけるために$${\alpha, \beta}$$でそれぞれ偏微分し求める

$$
\begin{align*}
\frac{\partial}{\partial \alpha} \sum^{n}_{i=1}(y_{i} - \alpha - \beta x_{i})^2 &= 0 \\
\frac{\partial}{\partial \beta} \sum^{n}_{i=1}(y_{i} - \alpha - \beta x_{i})^2 &= 0 \end{align*}
$$

を満たす$${\hat{\alpha},\hat{ \beta}}$$を求める

$$
\begin{align*}
\frac{\partial}{\partial \alpha} \sum^{n}_{i=1}(y_{i} - \alpha - \beta x_{i})^2 &= 0 \\ \sum^{n}_{i=1} 2(y_{i} - \alpha - \beta x_{i}) &= 0 \\
\sum^{n}_{i=1} y_{i} - n\alpha - \beta \sum^{n}_{i=1}x_{i} &= 0 \\
\frac{\sum^{n}_{i=1} y_{i}}{n} - \alpha - \beta\frac{\sum^{n}_{i=1}x_{i}}{n} &= 0 \\
\overline{y} - \hat{\alpha} - \hat{\beta} \overline{x} &= 0
\end{align*}
$$

よって$${\hat{\alpha}}$$は次のようにあらわされる

$$
\begin{align*}
\hat{\alpha} &= \overline{y} - \hat{\beta} \overline{x}
\end{align*}
$$

$$
\begin{align*}
\frac{\partial}{\partial \beta} \sum^{n}_{i=1}(y_{i} - \alpha - \beta x_{i})^2 &= 0 \\ \sum^{n}_{i=1} 2x_i(y_{i} - \alpha - \beta x_{i}) &= 0 \\
\sum^{n}_{i=1} x_iy_{i} - \sum^{n}_{i=1}\alpha x_i - \beta \sum^{n}_{i=1}x_{i}^{2} &= 0 \\
\frac{\sum^{n}_{i=1} x_iy_{i}}{n} - \alpha\frac{\sum^{n}_{i=1}x_{i}}{n} - \beta\frac{\sum^{n}_{i=1}x_{i}^{2}}{n} &= 0 \\
\overline{xy} - \hat{\alpha}\overline{x} - \hat{\beta} \overline{x^2} &= 0
\end{align*}
$$

$${\hat{\alpha}}$$を代入すると

$$
\begin{align*}
\overline{xy} - \hat{\alpha}\overline{x} - \hat{\beta} \overline{x^2} &= \overline{xy} - \left(\overline{y} - \hat{\beta} \overline{x}\right)\overline{x} - \hat{\beta} \overline{x^2} \\
&=  \overline{xy} -  \overline{x} \overline{y} - \hat{\beta}\left(\overline{x^2} - \overline{x}^2 \right) \\
&= \sigma_{xy} - \hat{\beta}\sigma_x^2= 0
\end{align*}
$$

よって$${\hat{\beta}}$$が求まる

$$
\begin{align*}
\hat{\beta} &= \frac{ \sigma_{xy} }{\sigma_x^2}
\end{align*}
$$

$${\hat{\alpha}}$$の式に代入することで同様に求めることができる

$$
\begin{align*}
\hat{\alpha} &= \overline{y} - \frac{ \sigma_{xy} }{\sigma_x^2}\overline{x}
\end{align*}
$$

誤差項の分散の推定

前提2より誤差項は平均0分散$${\sigma^2}$$の正規分布に従う
分散$${\sigma^2}$$の推定量$${\hat{\sigma}^2}$$を計算する。まず誤差項$${\epsilon_{i}}$$の標本平均$${\overline{\epsilon}}$$を求める

$$
\begin{align*}
\bar{\epsilon} = \bar{y} - \hat{\alpha} - \hat{\beta} \bar{x} \\
\end{align*}
$$

誤差項の平方和$${\sum^{n}_{i=1}\left(\epsilon_i - \bar{\epsilon}\right)^2}$$を求めると

$$
\begin{align*}
\epsilon_{i} - \bar{\epsilon} &= y_{i} - \bar{y}  - \hat{\beta}\left(x_i -  \bar{x}\right) \\
\sum^{n}_{i=1}\left(\epsilon_i - \bar{\epsilon}\right)^2 &= \sum^{n}_{i=1}\left(y_{i} - \bar{y}  - \hat{\beta}\left(x_i -  \bar{x}\right)\right)^2 \\
&= \sum^{n}_{i=1}\left(y_{i} - \bar{y}\right)^2  -2\hat{\beta}\sum^{n}_{i=1}\left(y_{i} - \bar{y}\right)\left(x_{i} - \bar{x}\right)
 + \sum^{n}_{i=1} \hat{\beta}^2 \left(x_i -  \bar{x}\right)^2 \\
&= n\sigma^2_y -2n\hat{\beta}\sigma_{xy} + n\hat{\beta}^2\sigma^2_x
\end{align*}
$$

$${\hat{\beta}}$$を代入すると

$$
\begin{align*}
\sum^{n}_{i=1}\left(\epsilon_i - \bar{\epsilon}\right)^2 &= n\sigma^2_y -2n \frac{ \sigma_{xy} }{\sigma_x^2}\sigma_{xy} + n \left(\frac{ \sigma_{xy} }{\sigma_x^2}\right)^2\sigma^2_x \\
&= n\sigma^2_y -2n \frac{ \sigma_{xy}^2 }{\sigma_x^2\sigma_y^2}\sigma_y^2 + n \frac{ \sigma_{xy}^2}{\sigma_x^2\sigma^2_y}\sigma^2_y \\ 
&= n\sigma^2_y\left(1 - \frac{ \sigma_{xy}^2 }{\sigma_x^2\sigma_y^2}\right) \\ 
&= n\sigma^2_y\left(1 - r_{xy}^2\right)
\end{align*}
$$

$${\hat{\sigma}^2}$$は自由度$${n-2}$$であることから平方和を$${n-2}$$で割ると求めることができる

$$
\begin{align*}
\hat{\sigma}^2 &= \frac{\sum^{n}_{i=1}\left(\epsilon_i - \bar{\epsilon}\right)^2}{n-2} \\
&= \frac{n}{n-2}\sigma^2_y\left(1 - r_{xy}^2\right)
\end{align*}
$$

パラメータ推定量の性質と平均・分散

$${\hat{\alpha}, \hat{\beta}}$$の平均、分散を求める
まずは$${\hat{\beta}}$$から算出

$$
\begin{align*}
\hat{\beta} &= \frac{ \sigma_{xy} }{\sigma_x^2} \\
&= \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}
\end{align*}
$$

$${y_{i} = \alpha + \beta x_{i} + \epsilon_{i}, \overline{y} = \alpha + \beta \overline{x} + \overline{\epsilon}}$$を代入

$$
\begin{align*}
\hat{\beta} &= \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\left(\alpha + \beta x_{i} + \epsilon_{i}-\left(\alpha + \beta \overline{x} + \overline{\epsilon}\right)\right)}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} \\ 
&= \frac{\beta\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2  + \sum^{n}_{i=1}\left(x_i-\overline{x}\right)\left(\epsilon_{i}-\overline{\epsilon}\right)}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} \\ 
&= \beta + \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} - \overline{\epsilon}\frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}
\end{align*}
$$

$${\sum^{n}_{i=1}\left(x_i-\overline{x}\right)=0}$$より

$$
\begin{align*}
\hat{\beta} &= \beta + \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} 
\end{align*}
$$

$${\epsilon_{i}}$$は正規分布に従うことから$${\hat{\beta}}$$も正規分布に従う。続いて平均と分散を求める

$$
\begin{align*}
E\left[\hat{\beta}\right] &= \beta + \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)E[\epsilon_{i}]}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}  \\
&= \beta
\end{align*}
$$

$$
\begin{align*}
V\left[\hat{\beta}\right] &= V\left[ \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}  \right]\\
&= V\left[ \frac{\epsilon_1\left(x_1-\overline{x}\right) + \epsilon_2\left(x_2-\overline{x}\right) + \cdots \epsilon_n\left(x_n-\overline{x}\right)}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}  \right]\\
&=  \frac{V[\epsilon_1]\left(x_1-\overline{x}\right)^2 + V[\epsilon_2]\left(x_2-\overline{x}\right)^2 + \cdots V[\epsilon_n]\left(x_n-\overline{x}\right)^2}{\left(\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2\right)^2} \\
&=  \hat{\sigma}^2\frac{ \sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}{\left(\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2\right)^2} \\
&=  \frac{\hat{\sigma}^2}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} \\
&=  \frac{1}{n}\frac{\hat{\sigma}^2}{\sigma_{x}^{2}}
\end{align*}
$$

以上より$${\hat{\beta}}$$は平均$${\beta}$$、分散$${ \frac{1}{n}\frac{\hat{\sigma}^2}{\sigma_{x}^{2}}}$$の正規分布に従う

$$
\begin{align*}
\hat{\beta} \sim N\left(\beta,  \frac{1}{n}\frac{\hat{\sigma}^2}{\sigma_{x}^{2}}\right)
\end{align*}
$$

続いて$${\hat{\alpha}}$$の平均と分散を計算する
$${\overline{y} = \alpha + \beta\overline{x}+\overline{\epsilon}, \hat{\beta} = \beta + \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}  }$$を代入する

$$
\begin{align*}
\hat{\alpha} &= \overline{y} - \hat{\beta} \overline{x} \\ 
&= \alpha + \beta\overline{x}+\overline{\epsilon} - \left(\beta + \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} \right)\overline{x} \\
&= \alpha + \overline{\epsilon} - \left(\frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} \right)\overline{x}
\end{align*}
$$

$${\overline{\epsilon}, \epsilon_{i}}$$は正規分布に従うことから$${\hat{\alpha}}$$も正規分布に従う。続いて平均と分散を求める

$$
\begin{align*}
E\left[\hat{\alpha}\right] &= \alpha + E[\overline{\epsilon}] - \frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)E[\epsilon_{i}]}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2}\overline{x}  \\
&= \alpha
\end{align*}
$$

$$
\begin{align*}
V\left[\hat{\alpha}\right] &= V\left[\alpha + \overline{\epsilon} - \left(\frac{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)\epsilon_{i}}{\sum^{n}_{i=1}\left(x_i-\overline{x}\right)^2} \right)\overline{x}\right] \\
&= V[ \overline{\epsilon}] + V[\epsilon_{i}] \frac{1}{n}\frac{\overline{x}^2}{\sigma^{2}_{x}} \\
&= \frac{\hat{\sigma}^2}{n} + \frac{\hat{\sigma}^2}{n}\frac{\overline{x}^2}{\sigma^{2}_{x}} \\
&= \frac{\hat{\sigma}^2}{n}\left(1+\frac{\overline{x}^2}{\sigma^{2}_{x}}\right)
\end{align*}
$$

以上より$${\hat{\alpha}}$$は平均$${\alpha}$$、分散$${ \frac{\hat{\sigma}^2}{n}\left(1+\frac{\overline{x}^2}{\sigma^{2}_{x}}\right)}$$の正規分布に従う

$$
\begin{align*}
\hat{\alpha} \sim N\left(\alpha, \frac{\hat{\sigma}^2}{n}\left(1+\frac{\overline{x}^2}{\sigma^{2}_{x}}\right)\right)
\end{align*}
$$

パラメータ推定量の区間推定

上記で求めた平均、分散を使用し区間推定や検定を実施することが可能
例として有意水準95%で$${\alpha, \beta}$$の区間推定を行ってみる

$$
\begin{align*}
\hat{\alpha} - t_{n-2}(0.025) \sqrt{\frac{\hat{\sigma}^2}{n}\left(1+\frac{\overline{x}^2}{\sigma^{2}_{x}}\right)} \leq \alpha \leq \hat{\alpha} + t_{n-2}(0.025) \sqrt{\frac{\hat{\sigma}^2}{n}\left(1+\frac{\overline{x}^2}{\sigma^{2}_{x}}\right)}
\end{align*}
$$

$$
\begin{align*}
\hat{\beta} - t_{n-2}(0.025) \sqrt{\frac{1}{n}\frac{\hat{\sigma}^2}{\sigma_{x}^{2}}} \leq \beta \leq \hat{\beta} + t_{n-2}(0.025) \sqrt{\frac{1}{n}\frac{\hat{\sigma}^2}{\sigma_{x}^{2}}}
\end{align*}
$$

pythonでのシミュレーション

シミュレーション内容

t分布の当てはまり具合を下記の条件下でpythonを用いたシミュレーションを行う
母集団：$${\beta = 0.416, \alpha = -0.363, \sigma^2 \sim N(0, 0.043)}$$で定義される
$${y = 0.416x - 0.363 + \sigma^2}$$
標本集団：上記の母集団からサンプリングした$${x,y}$$100個
標本集団の数：10,000個
シミュレーション手順
１．100個の標本集団から推定した$${\hat{\alpha}, \hat{\beta}}$$の値と分散からt値を求める
２．同じ作業を10,000回繰り返す
３．２で溜まった10,000回分のt値をプロットし、有意水準90%, 95%, 99%を棄却する数がそれぞれ1,000件、500件、100件になるか確かめる

結果

10,000件の$${\beta}$$のt値をプロットした結果がこちら

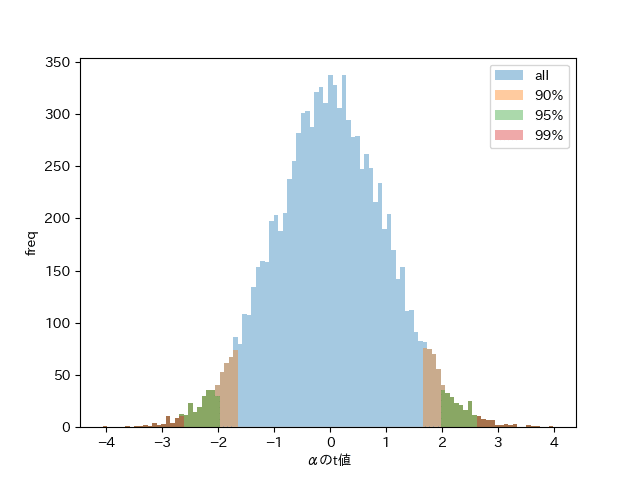
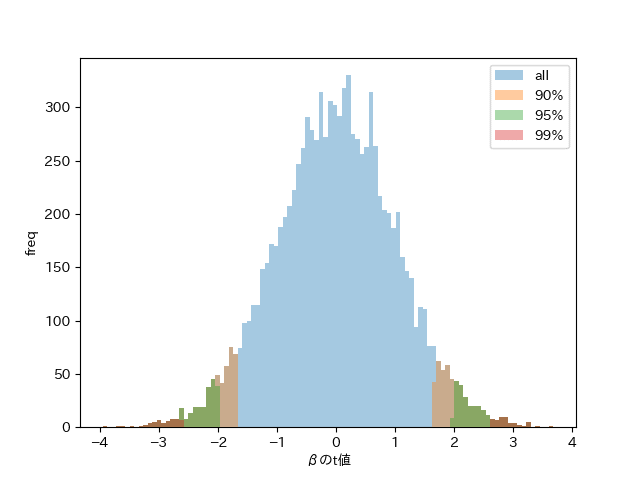
そして棄却した数は下記の集計表である
それぞれ理論値に近い棄却数となっており、$${\hat{\alpha}, \hat{\beta}}$$の平均値、および分散の値は正しそう

$$
\begin{array}{lrrr}
& 90\% & 95\% & 99\%\\ \hline
\hat{\alpha} の棄却数& 1,045 & 499 & 101\\
\hat{\beta} の棄却数& 1,031 & 527 & 109
\end{array}
$$