ネイピア数ともいわれる「自然対数の底」とは、$${e=2.71828…}$$と無限に続く無理数です。この$${e}$$について言いたいことがたくさんあって、自分はこの数が大好きで、その愛をつらつらと述べていこうと思っています。

対数はルートと同じ

そもそも対数ってのはなんでしょうか。
$${\log}$$は高校で習うが何だったか、なじみの無い人もいると思います。
突然$${\log_2 3}$$といわれて、説明できる方が少数派ではないかと思われます。
ごちゃごちゃ詳しく説明することもできると思いますが、ここでは簡単に掴んでもらえるようルート$${\sqrt{}}$$をつかって$${\log}$$を捉えていこうと思います。

$${\sqrt{3}}$$とはなんでしょう。これは「二乗して3になる数」と答えられると思います。これを図に表してみると次のようになります。

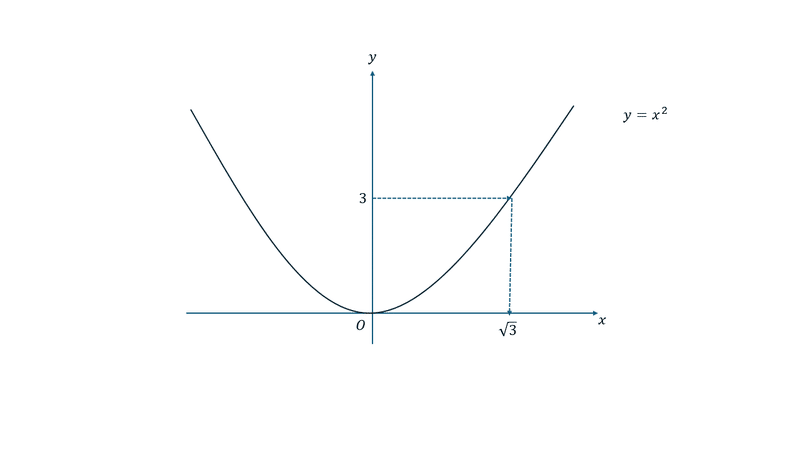
このように$${y}$$座標が3のところとグラフがぶつかるところを$${\sqrt{3}}$$と表そうというのがルートの決まりでした。
つまり、$${3=(\sqrt{3})^2}$$でした。
このことを踏まえて次の図をみてください。

指数関数$${y=2^x}$$に対して、$${y}$$座標が3のところとグラフがぶつかるところを$${\log_2 3}$$と書こうというのが$${\log}$$の約束です。2の部分を「底」、3の部分を「真数」といいます。
つまり、$${3=2^{\log_2 3}}$$であるとわかります。
このことから最初の問に堂々と答えることができます。
$${\log_2 3}$$とは「2を何乗すれば3になるか表す数」といえます。
例えば、$${\log_2 4=2}$$だし、$${\log_3 27=3}$$です。
この例から次の式が納得できるはずです。
$${a,M}$$を正の数とし、さらに$${a}$$は1と異なるとします。このとき、$${M=a^{\log_{a} M}}$$が成立します。

「逆関数」の考えから対数はルートと同じ発想であるよっていうのをみてみました。難しそうに思える式も理解してもらえたと思います。
さて、その上で自然対数の底$${e}$$とはなんでしょう。これもいろいろな説明ができますが、「微分」を中心に次の記事で考えていこうと思います。