リュディアです。引き続き三角比(三角関数)について見てみます。今回は高校1年生の三角比の授業を逸脱します。私個人の経験から知っておくと役に立ちますし今後の見通しもよくなります。ゆっくり見ていきましょう。sin, cos, tan で角の大きさが0や90°のときの扱いも明確になります。

皆さんは単位円をしっていますか？x-y座標系に単位円を書いてみましょう。単位円とは半径1の円のことでx-y座標系に重ねて書く場合は単位円の中心を原点Oに重ねます。単位円とx軸との交点は (1,0) と(-1, 0)です。単位円とy軸との交点は(0, 1) と (0, -1)です。ここまでは大丈夫ですね。

次に単位円に直角三角形を追加した図を見てください。直角三角形は30°、60°の角を持つもので右下に直角、左下に30°の角をもつように配置します。このとき三角形の頂点と単位円の交点Aの座標を求めてください。

できましたか？次の図と照らし合わせてみてください。おそらく多くの人は30°、60°の直角参加系の比を使って座標を求めたと思います。しかしこの座標をよく見ると三角形の左下の角と三角比を使えば簡単に求められることに気づくはずです。

そうです。単位円上の座標は X座標が cos、Y座標が sin で表現できるのです。この例では30°という角を使いましたが一般化してみます。次の図でAの座標を求めてください。

できましたか？簡単ですね。次のようになります。

つまりcos, sin は角が大きくなると単位円上を反時計周りに回転する点を表現するわけです。では角の大きさが0の場合、90°の場合を考えてみましょう。まず0の場合からです。角の大きさが0のとき図中の緑線のようになります。このときの単位円との交点の座標が (cos0, sin0)になることからcos0 = 1, sin0 = 0 となります。なりますというよりは、このように決めると都合がよいという感じですね。

同様に角の大きさが90°の場合を考えます。自分で絵を書いて考えられる方は自分でやってみてください。

角の大きさが90°のとき図中の緑線のようになります。このときの単位円との交点の座標が (cos90°, sin90°)になることからcos90° = 0, sin90° = 1 となります。これで cos, sin については明確になったと思います。では tan はどうなるのでしょうか？次の図を見てください。

sin, cos のような単位円上の点ではなく x = 1 の直線上を移動する点のY座標がtanθになります。ではsin, cos と同様に角の大きさが0、90°の場合を見てみましょう。まず角の大きさが0の場合から見てみます。

角の大きさが0の時、図中の緑線のようになります。このときの座標が (1, tan0)になることからtan0 = 0となります。わかりやすいですね。次が問題の90°の場合です。

90°のときは緑線のようになるのですが tan が x=1 の直線上の点であると考えると永久に交わらないですね。つまり定義できないということはこういうことなのです。そもそも土俵にのっていないということです。

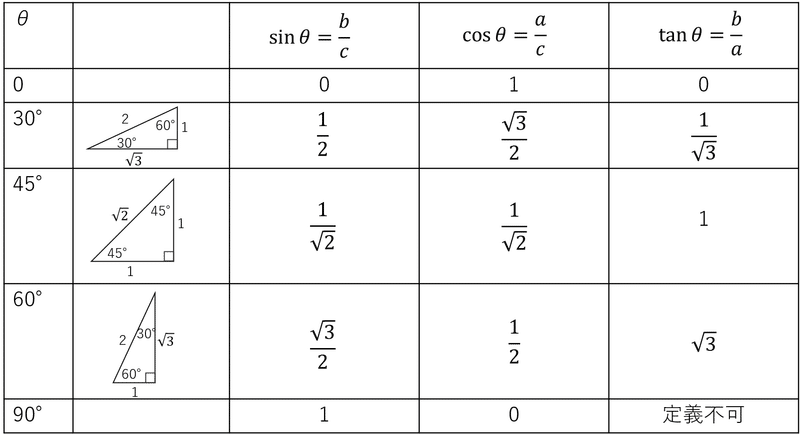
ここまでの内容で皆さんは図的なイメージを頭に描いて三角比の具体的な値を計算することができます。手計算で同じように求めていたとして頭に図的なイメージがある人と単に手先で計算しているだけの人では意味が違います。しっかりと図的なイメージを持ってください。最後に再度、表をのせておくので自分で単位円を書いて確かにこの値になる、ということを確認してもらいたいと思います。

では、ごきげんよう。