Cover Photo by Christopher Burns on Unsplash

正規分布で近似しよう

前回は、二項分布のおさらいまでを書きました。二項分布を理解したうえで正規分布へと話は進むのですが、正規分布の確率密度関数を高等学校で学習するわけではありません。二項分布は、試行回数（N）が大きい時に、正規分布で近似できるという性質があります。そのことを使って、統計的な判断（要するに簡易的な検定）をしようとしています。すなわち、

1. 平均±標準偏差×kの区間の値が出現する割合は決まっていて、k=1のときおよそ68.3％、k=2のときおよそ95.4%、k=3のときおよそ99.7%であること（「解説」には「シグマの法則」と書かれています）を理解する。

2. そのうえで、二項分布で計算された平均と標準偏差を用いて、Z標準化を行い、変換されたzの大きさから統計的な判断（簡易的な検定）を行う。

という手順を踏むことになります。

サイコロを720回振る

具体的な数値でやってみましょう。「解説」では、次のような例が取り上げられています。
＞さいころを720 回投げたとき，1 の目が出る回数が100 回以下となる確率などを取り扱うことが考えられる。
おお、Nが一気に大きくなりましたね。1の目がちょうど100回出る確率は、二項分布では、

$$
_{720}C_{100}(\frac16)^{100}(\frac56)^{620} = 0.00527…
$$

と計算できますが、コンピュータを使わずに計算しなさいと言われたら確実に死にますね。そこで、Z変換をします。確認すると、Z変換とは、確率変数からその平均値（期待値）を引いて、標準偏差で割るという変換です。

$$
Z = \frac{X - \mu}{\sigma}
$$

さきほどの、サイコロを720回振るという設定の場合、平均値は$${np=720\times \frac16=120}$$であり、分散は$${np(1-p)=720\times \frac16 \times \frac56 = 100}$$です。標準偏差は分散の平方根なので、$${10}$$になります。これを用いて、$${x=100}$$をZ変換すると、$${z = (100-120)/10=-2}$$となります。
前述の「シグマの法則」によれば、標準正規分布において、zが-2～2におさまる確率（つまり平均±標準偏差×２の範囲）はおよそ95.4％でした。xが100以下になる確率は、Z変換したzが-2以下になる確率にほぼ等しいと考えられます。よって、$${(1-0.954)/2=0.023}$$となり、「さいころを720回振ったとき、1 の目が出る回数が100 回以下となる確率」は、およそ2.3％と考えられます。

二つの分布の比較

下の表は、実際に二項分布（試行回数720、成功確率1/6）と、正規分布（平均120、分散100）で、それぞれの値が出現する確率を計算したものの一部です。左端の列（90, 91,…）が、確率変数の値、その右が、順に二項分布、正規分布でその値が出現する確率（確率質量としての値）、右端が、二項分布と正規分布の確率の差です。若干のずれはあるものの、両者の差は10のマイナス4乗未満で、きわめて小さいことが分かります。

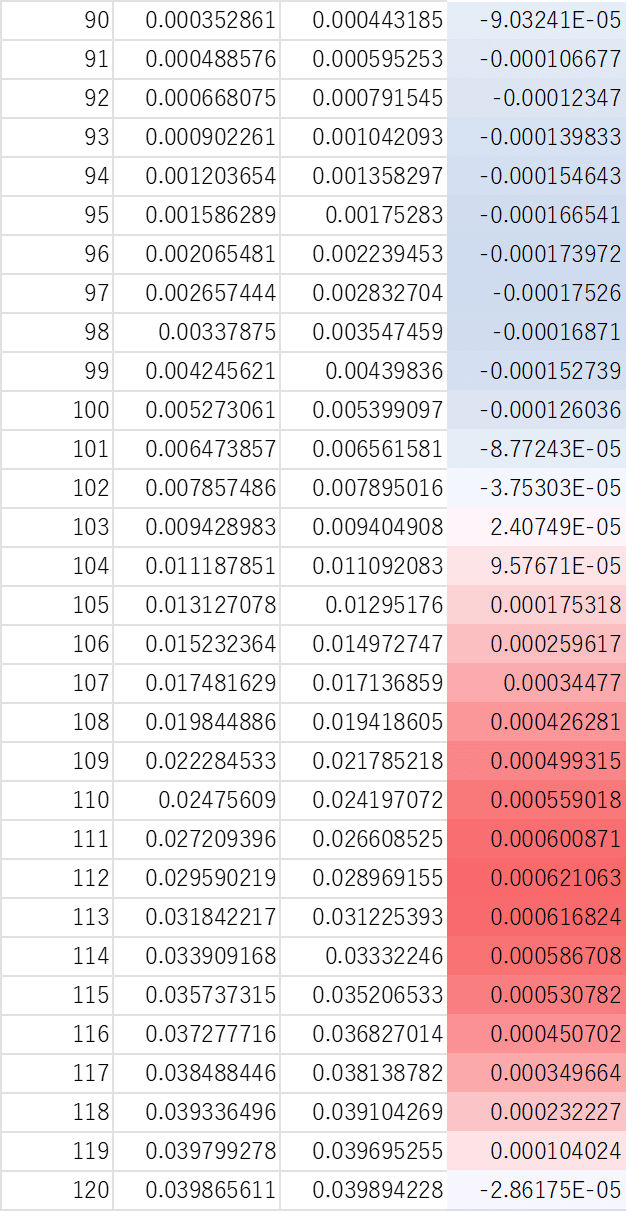
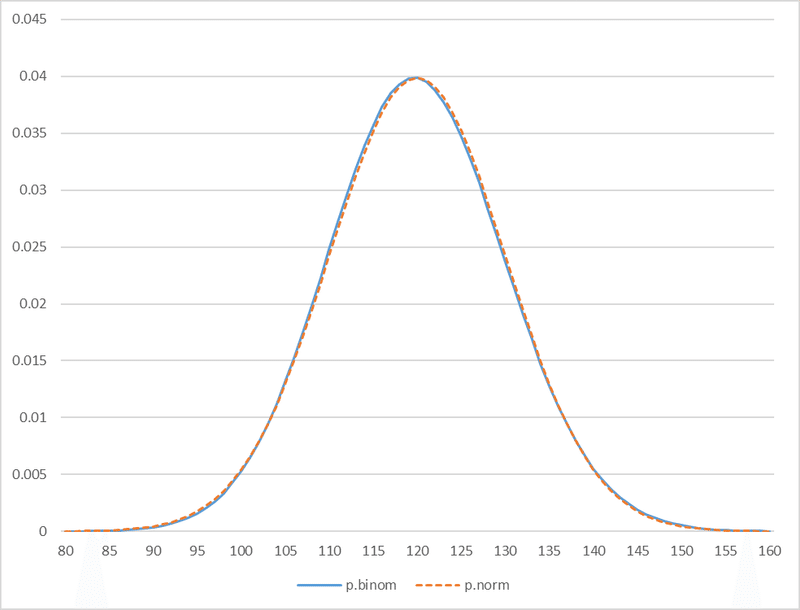
平均値付近を取り出してグラフにすると、ほぼ重なっていることが確かめられます。なかなか楽しいですね。「解説」にも、

とありますから、上に描いたような表やグラフを作ってみる、という活動が授業中に扱われるのかもしれません。楽しそうですね。こういうのが好きな生徒にとっては、という限定付きですが。

というわけで、ここまで、試行回数Nが十分に大きい時に、二項分布が正規分布で近似できることを確かめてきました。この後、仮説検定と区間推定の話が続くのですが、少々やっかいなので、次回に回します。