基本情報技術者試験の教科書の、わりとはじめの方に出てくる算術シフト。
その中でもひときわ奇妙な「負の数の右算術シフト」に関して、納得できる説明がネットでパッと出てきませんでした。Yahoo!知恵袋なんか「手で考えろ」ですからね。絶望的ですね。なので、わたしが自分で納得できるまで考えた結果をここに記しておこうと思います。わたし自身まだまだ初学者ですが、ないものは作るしかありません。想定する読者は同じところで、学習の途中で立ち止まっている人ですから、タイトルより他の部分に関しては説明しません。

1.図形的な説明

　まず思い返してほしいのは、負の数が補数によって表現されているということです。もっと言えば、ある量の数（定数）との差という形で表現されているということです。たとえば下の図では、-4（空白の部分）が定数（いまの場合16）に対する差によって表されています。

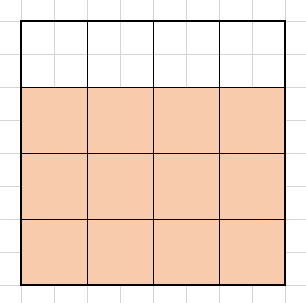
負の数が定数からの差という形で示されている以上、空白の部分を縮小させた時にも、定数にあたる部分は、元と同じ大きさを保っていなければなりません。たとえば上の図形を4分の1サイズに縮小してみます。

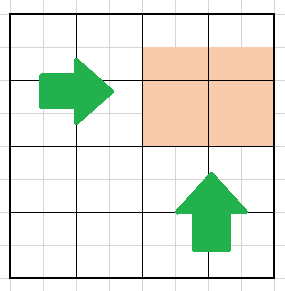
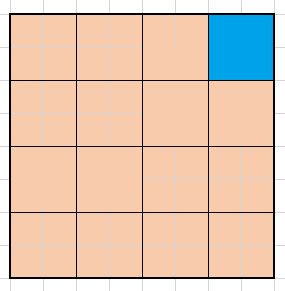
そうすると、先ほど-4を表していた部分は-1に相当する大きさ（下図の青色の部分）になりました。

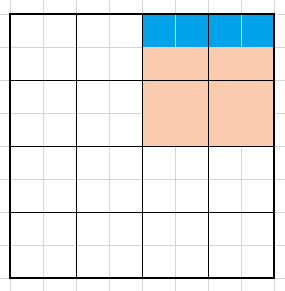
　しかし、同時に定数（16）の残りを埋めている部分も縮小され、謎の空白ができてしまっています。これでは、青色の部分が-1を表していることになりません。

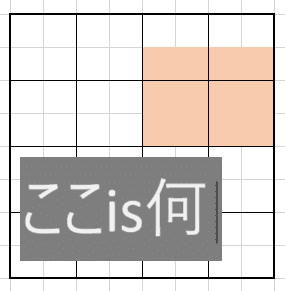
青色の部分が-1を表すようにするためには、この謎の空白をきっちり埋める必要が出てくるわけです。下図のように。

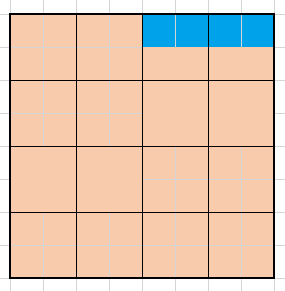
青色の部分を寄せると、定数（16）に対して1つの差（-1）が表現できていることがわかります。

この「除算によって同時に減ってしまった『空白に対する残りの部分』を埋めるもの」が、負の数の右算術シフトで送られてくる、あの奇妙な1の正体なのです。

2.同じことを数式で説明します

整数$${t_1}$$と、$${t_1}$$との和が定数$${k}$$になるような整数$${t_2}$$とを考えます。

$$
\begin{array}{}t_1+t_2&=&k\end{array}
$$

左辺を変形すると

$$
\begin{array}{}\dfrac 1 {2^n}t_1+\dfrac {2^n-1} {2^n}t_1+t_2&=&k\end{array}
$$

右算術シフトでやりたいのは$${2^n}$$での除算ですから、$${\dfrac 1 {2^n}t_1}$$は最終的に求めたい数ですね。そこで$${\dfrac 1 {2^n}t_1=t_3}$$とおくと

$$
\begin{array}{}t_3+\dfrac {2^n-1} {2^n}t_1+t_2&=&k\end{array}
$$

最初の定義から、$${t_1=k-t_2}$$ですから代入して

$$
\begin{array}{}t_3+\dfrac {2^n-1} {2^n}(k-t_2)+t_2&=&k\end{array}
$$

整理して

$$
\begin{array}{}t_3+( \dfrac 1 {2^n}t_2+\dfrac {2^n-1} {2^n}k)&=&k\end{array}
$$

定義上、このカッコでくくった部分が$${t_3}$$の補数にあたる数のはずですが、$${1/2^n}$$された$${t_2}$$だけではなくて、$${\dfrac {2^n-1} {2^n}k}$$も足されてますよね？　これが右算術シフトの1で増えてる部分なんです。マジで。

3.マジかどうか試してみます

符号ビットを含めて8ビットの固定小数点レジスタで、-16を表現すると
（$${(00010000)_2}$$と書いて、ビット反転して$${(11101111)_2}$$、で1足して）
$${(11110000)_2}$$
になります。これを$${1/2^2}$$にする、つまり2ビット右に算術シフトしたら、答えは-4になるはずですね。
$${(11111100)_2}$$
ビット反転して$${(00000011)_2}$$、1足して$${(00000100)_2}$$なので確かに-4なのですが、右シフトの過程で符号ビットがなんか足しましたね。具体的には
$${(11000000)_2}$$
を足してきました。

　これが何なのか考えるために、まず現在の方式において、負の整数がどんな定数の補数として表されているか、確認してみましょう。さっき使った16と-16（として解釈される2進数）を足すと、$${(11110000)_2}$$＋$${(00010000)_2}$$＝$${(100000000)_2}$$。十進法で256ですから、負の整数は256に対する補数として表されているということになります。前項の数式

$$
\begin{array}{}t_3+( \dfrac 1 {2^n}t_2+\dfrac {2^n-1} {2^n}k)&=&k\end{array}
$$

に当てはめれば、$${k=256}$$、4分の1にしているので$${n=2}$$。前項までの説明が正しければ、算術シフトによって生まれてしまう空白を埋めるために、$${\dfrac {2^n-1} {2^n}k=\dfrac 3 4 \cdot256=192}$$が足されているということになります。

ここで$${(11000000)_2}$$を単純に、正の整数として十進法に直してみると……

!