問題はこちら：

答え：以下のような放物線

　問題の手順で穿っていった点は上式のような放物線を描きます。図にするとこういう感じです：

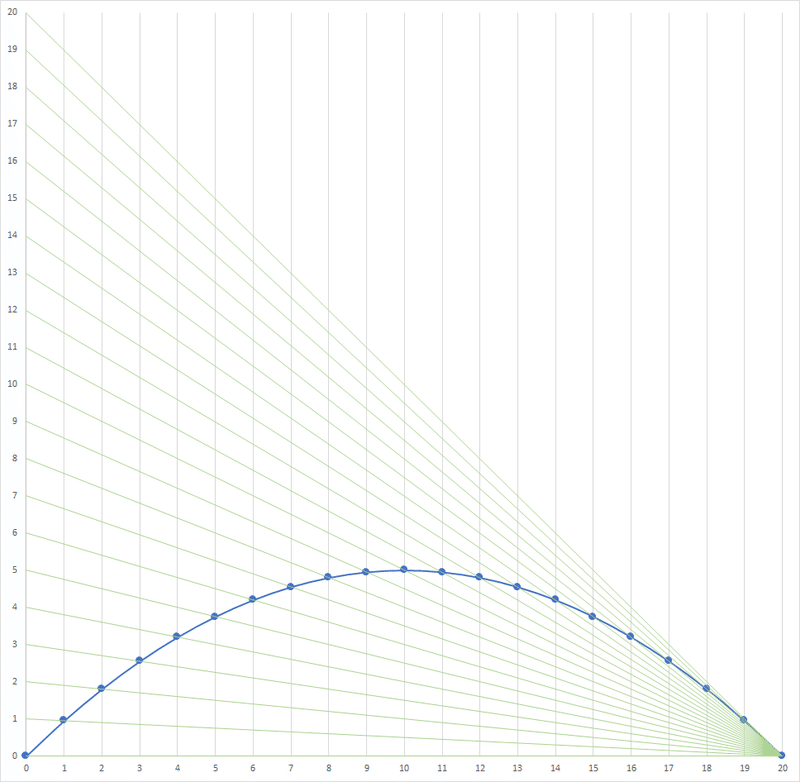
どうしてこのプロットが放物線になるか、理由を説明します。

解説：媒介変数を上手く使おう

　今回の問題のように2つの直線の交点が一定のルールでどんどん出来上がっていく、そういう動的な交点を考える時には「媒介変数」を使うと考えやすくなります。

　まず交差する2つの直線を媒介変数で定義してみましょう。X軸上の点を通ってY軸と平行な縦線は媒介変数tを用いて、

と表せます。ここでtは0以上P以下の値です。

　次にY軸上の格子点と点Pを通る直線も同じ媒介変数tを用いて表してみます：

上図のようにtは直線のY切片で、傾きは横がPで縦が-tですから、

ですね。

　後は2つの式を統合してtを消してyとxだけの式にします。これはx=tを上式に代入すれば出来ますね：

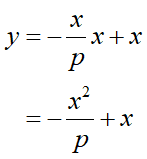
このように2次曲線の式になりました。

　媒介変数tで表されたxとyは、tを上手く消せる場合はy=f(x)という関数（陽関数）に出来ます。上は上手くいく例の一つというわけです。tを上手く消せないケースも多々あります。そういうのは媒介変数としてxとyを分離して表現するしかありません（陰関数）。

深掘：点Pが右に移動するとどうなるか？

　問題の点Pは固定でしたが、点Pが媒介変数tに比例して右に移動すると交点はどういう軌跡を描くでしょうか？これも考え方は解説と全く同じです。

　点Pに向かう直線が今回の問題と少し変わってきます。点Pの初期位置をp0とし右に向かう速度をsとしておきましょうか。そうすると点Pの位置は、

と表現出来ます。よってyiから点Pに向かう直線は、

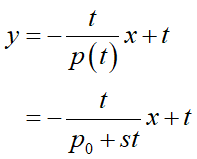
となります。x=tは変わらないので、tに代入すると、

分母にxがあるちょっと変わった式が出てきました。これをグラフにすると、

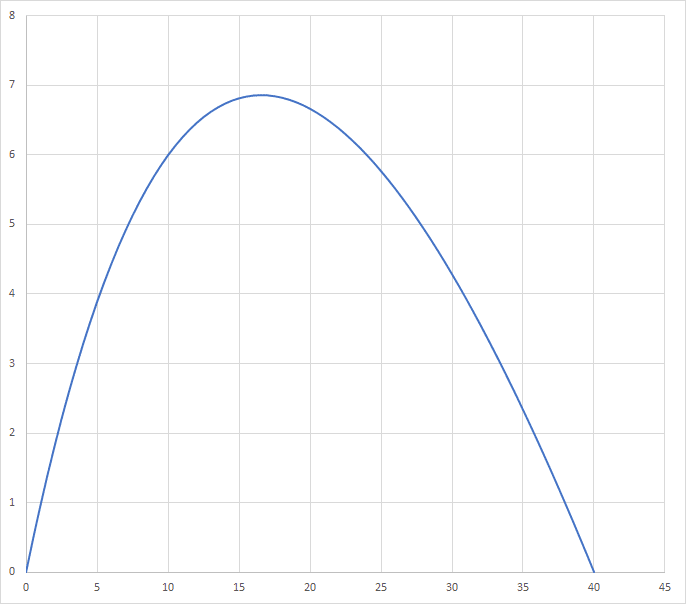
このような2次曲線が左に傾いたような曲線になるのがわかりました。点Pが固定だと2次曲線、動くと違う曲線に。なかなかに興味深いものです。

　こうなると、点Pが上に動いた場合はとか、点Pが円を描いたらどうなるだろう、またx=tじゃなくて、(x,y)=(t,0)を通る直線との交点だったらどうなるだろう、など試してみたい発想が色々と出てきますよね。交点の軌跡って面白いんです(^-^)

　ではこういう2つの直線の交点はどう活用されているのか？例えば「リンク機構」がその一例に挙げられます：

リンク機構というのは、2つ以上の物が何らかの接点で繋がり協調して動く事で、回転や往復運動などの動作を別の動作に変換する事ができる工学的な機構を言います。有名な所だと車のワイパーがありますね。ワイパーは根元でモーターが回転しているのですが、それがリンク機構によって往復運動に変換されています。ロボット工学や工場のラインなどではこのリンク機構が多用されており、その基本的な所は今回の問題のような交点の軌道などだったりします。

　皆さんも点Pの動かし方などを工夫してみて、方眼紙に面白い曲線が描けましたら是非教えて下さい！ではまた(^-^)/