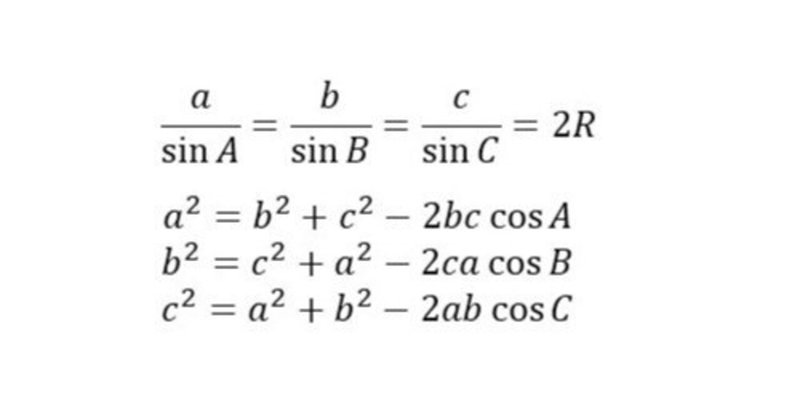
高校数学をプログラミングで解く(数学I編)「2-4 正弦定理と余弦定理」
はじめに
今回は、数学Iで学ぶ「正弦定理と余弦定理」について、正弦定理と余弦定理を用いた三角形に対する外心と外接円を描くプログラムを作成します。
正弦定理と余弦定理
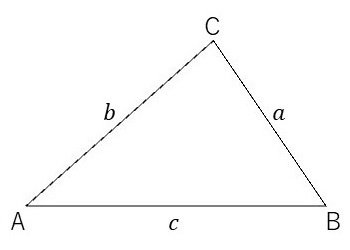
まず、図1の△ABCを例として正弦定理と余弦定理についてまとめておきます。
正弦定理
$$
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
$$
ここで、$${R}$$は△ABCの外接円の半径を表しています。
余弦定理
$$
a^2 = b^2 + c^2 - 2bc \cos A, b^2 = c^2 + a^2 -2ca \cos B, c^2 = a^2 + b^2 -2ab \cos C
$$
$$
\cos A = \frac{b^2 + c^2 - a^2}{2bc}, \cos B = \frac{c^2 + a^2 - b^2}{2ca}, \cos C = \frac{a^2 + b^2 - c^2}{2ab}
$$
三角形の外心と外接円(再考)
記事『高校数学をプログラミングで解く(数学A編)「2-3 三角形の五心」』で、図1で示した△ABCに対して外心と外接円を描くプログラムを作成しました。今回は三角形の外心の座標や外接円の半径を正弦定理と余弦定理を用いて算出し、それらをもとに△ABCの外心と外接円を描くプログラムを作成してみます。
三角形の準備
△ABCを以下のようにします(図1と同じものです)。
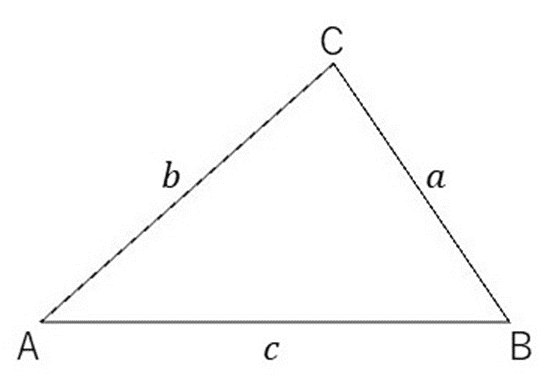
特に△ABCの辺の長さの比が$${a:b:c=4:5:6}$$となるようにします。
頂点の座標位置
図2の三角形を描くために、各頂点の座標位置を求めます。以下のように、頂点Aを原点とし、頂点Aと頂点Bを結んだ直線を右向き正とする$${x}$$軸、その直線と垂直に交わり、頂点Aを通る直線を上向き正とする$${y}$$軸とします。
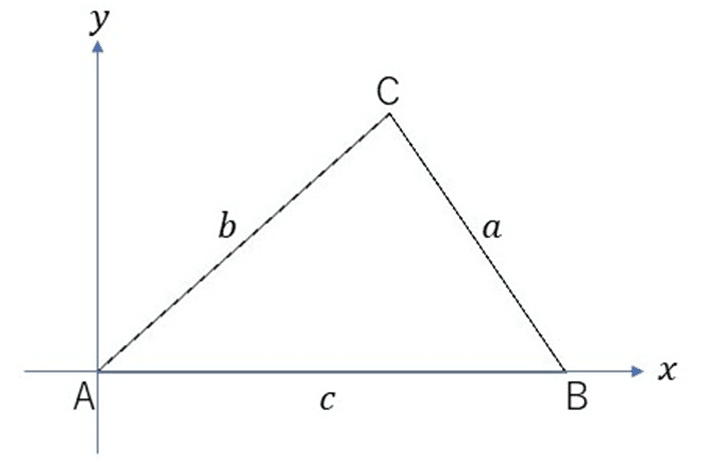
その結果、頂点Aの座標を$${(0,0)}$$、頂点Bの座標を$${(c,0)}$$と置くことができます。
頂点Cの座標位置
∠Aに対して余弦定理を用いると、$${\cos A}$$は
$$
\cos A = \frac{b^2 + c^2 - a^2}{2bc}
$$
で表すことができます。また、$${\sin^2 A + \cos^2 A = 1}$$より、
$$
\sin A = \sqrt{ 1 - \cos^2 A}
$$
となります。これらの結果を用いると、頂点Cの座標$${(x_C, y_C)}$$は、
$$
x_C = b \cos A, \ y_C = b \sin A
$$
と表すことができます。
三角形を描くプログラム
三角形の3つの頂点の座標がわかりましたので、この三角形を描くプログラムを作成しておきます。各辺の長さをそれぞれ
$$
a=200, \ \ b=250, \ \ c=300
$$
として描きます。
// 辺の長さの比が4,5,6の三角形を描く
void setup(){
size(650, 650); // キャンバスの大きさを指定する
translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
scale(1,-1); // y軸正の向きを下向きから上向きに反転する
background(255,255,255); // 背景を白色にする
noFill(); // 図形の塗りつぶしなし
noLoop(); // 繰り返し処理をしない
// 三角形の辺の長さ
float a, b, c;
a = 200.0;
b = 250.0;
c = 300.0;
// cosA, sinA(余弦定理より)
float cA = (b*b+c*c-a*a)/2.0/b/c;
float sA = sqrt( 1.0-cA*cA );
// 三角形の頂点の座標
float A_x, A_y, B_x, B_y, C_x, C_y;
A_x = 0.0;
A_y = 0.0;
B_x = c;
B_y = 0.0;
C_x = b * cA;
C_y = b * sA;
// 三角形を描く
triangle(A_x, A_y, B_x, B_y, C_x, C_y);
}ソースコード1 三角形を描くプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「drawTriangle2」としています)、テキストエディタ部分に書いて実行すると、実行ウィンドウのキャンバスに三角形が描かれます。

外接円の半径
外接円の半径$${R}$$は、正弦定理を用いると、
$$
R=\frac{a}{2 \sin A}
$$
と求めることができます。
外心の座標位置
外心の定義は「△ABCの3辺の垂直二等分線が交わる点」でした。これを考慮して、外心Oから辺ABに下した垂線が交わる点をDとして直角三角形ADOを考えます(図6)。
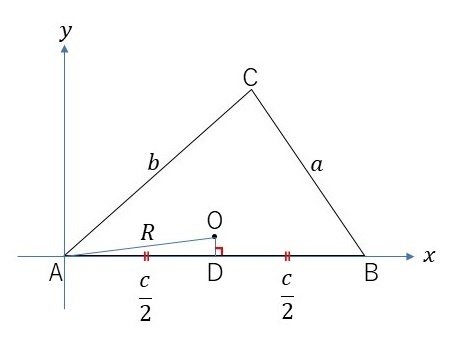
辺AOの長さはちょうど外接円の半径と一致し、また辺ADの長さは$${c/2}$$となるので、三平方の定理より
$$
\mathrm{DO} = \sqrt{R^2-\frac{c^2}{4}}
$$
となります。しがたって、外心Oの座標$${(x_O, y_O)}$$は、
$$
x_O = \frac{c}{2}, \ y_O = \sqrt{R^2-\frac{c^2}{4}}
$$
で与えられます。
外心と外接円を描くプログラム
外接円の半径$${R}$$と外心Oの座標$${(x_O,y_O)}$$がわかりましたので、あとはProcessingで円を描くための関数 circle を用いれば外接円を描くことができます。ソースコード1に追記する形で三角形の外心と外接円を描くプログラムを作成します。
// 辺の長さの比が4,5,6の三角形に外心と外接円を描く
void setup(){
size(650, 650); // キャンバスの大きさを指定する
translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
scale(1,-1); // y軸正の向きを下向きから上向きに反転する
background(255,255,255); // 背景を白色にする
noFill(); // 図形の塗りつぶしなし
noLoop(); // 繰り返し処理をしない
// 三角形の辺の長さ
float a, b, c;
a = 200.0;
b = 250.0;
c = 300.0;
// cosA, sinA(余弦定理より)
float cA = (b*b+c*c-a*a)/2.0/b/c;
float sA = sqrt( 1.0-cA*cA );
// 三角形の頂点の座標
float A_x, A_y, B_x, B_y, C_x, C_y;
A_x = 0.0;
A_y = 0.0;
B_x = c;
B_y = 0.0;
C_x = b * cA;
C_y = b * sA;
// 三角形を描く
triangle(A_x, A_y, B_x, B_y, C_x, C_y);
// 外接円の半径(正弦定理より)
float R = a / 2.0 / sA;
// 外心の座標
float O_x, O_y;
O_x = c / 2.0;
O_y = sqrt(R*R-c*c/4.0);
// 外接円を描画する
stroke(0,0,255);
circle(O_x, O_y, 2.0*R);
// 外心を描画する
strokeWeight(5.0);
point(O_x, O_y);
}ソースコード2 外心と外接円を描くプログラム
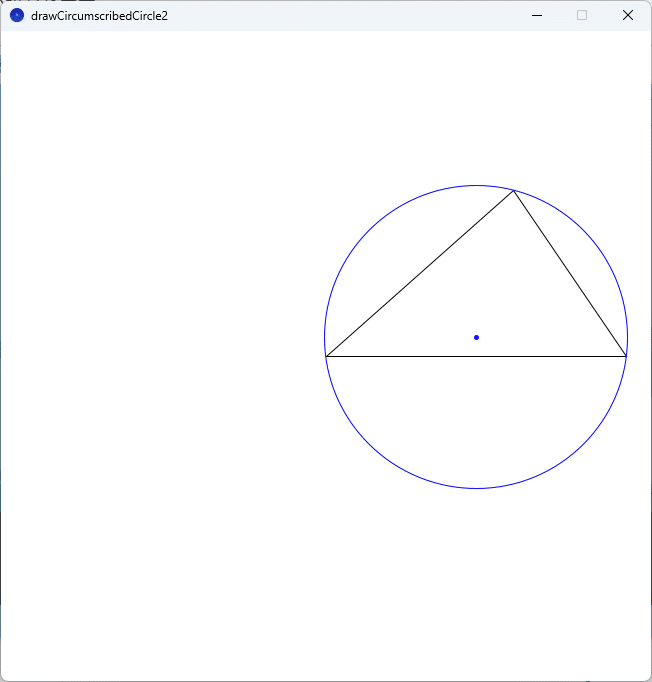
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「drawCircumscribedCircle2」としています)、テキストエディタ部分に書いて実行すると、実行ウィンドウのキャンバスに三角形とその外心と外接円が描かれます。
まとめ
今回は、数学Iで学ぶ「正弦定理と余弦定理」について、正弦定理と余弦定理を用いた三角形に対する外心と外接円を描くプログラムを作成しました。
記事『高校数学をプログラミングで解く(数学A編)「2-3 三角形の五心」』では、三角形の頂点の座標を三平方の定理を用いて導出し、また、外心の座標や外接円の半径については、外心の定義通り、各辺の垂直二等分線の方程式を導出してそれらを連立させて外心の座標を求め、その後外接円の半径を求めました。
今回は三角形の頂点の座標を余弦定理を用いることで導出し、外心の座標や外接円の半径については、まず正弦定理より外接円の半径を導出し、その後、外心の座標を導出しました。
記事『高校数学をプログラミングで解く(数学A編)「2-3 三角形の五心」』で導出した方法より、今回の正弦定理や余弦定理を用いて導出した方法がより簡単に感じたのではないでしょうか。
参考文献
改訂版 教科書傍用 スタンダード 数学I(数研出版、ISBN9784410209178)
この記事が気に入ったらサポートをしてみませんか?
