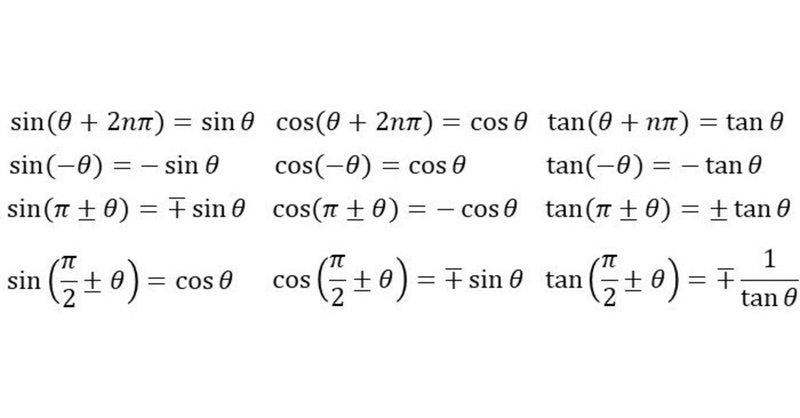
高校数学をプログラミングで解く(数学II編)「3-3 三角関数の性質」
はじめに
今回は、数学IIで学ぶ「三角関数の性質」について、三角関数の性質についてそれらが成り立っているかどうかを確かめるプログラムを作成します。
三角関数の性質
まず、三角関数の性質について解説しておきます。
三角関数の性質
以下、$${n}$$は整数、複合同順とします。
$$
\begin{array}{rl}
\mathrm{①} & \sin(\theta+2n\pi) = \sin \theta \ \ \cos(\theta+2n\pi) = \cos \theta \ \ \tan(\theta+n\pi) = \tan \theta \\ \\
\mathrm{②} & \sin(-\theta) = -\sin \theta \ \ \cos(-\theta) = \cos \theta \ \ \tan(-\theta) = -\tan \theta \\ \\
\mathrm{③} & \sin(\pi \pm \theta) = \mp \sin \theta \ \ \cos(\pi \pm \theta) = -\cos \theta \ \ \tan(\pi \pm \theta) = \pm \tan \theta \\ \\
\mathrm{④} & \sin(\frac{\pi}{2} \pm \theta) = \cos \theta \ \ \cos(\frac{\pi}{2} \pm \theta) = \mp \sin \theta \ \ \tan(\frac{\pi}{2} \pm \theta) = \mp \frac{1}{\tan \theta}
\end{array}
$$
三角関数の性質を確かめる
三角関数の性質は、記事『高校数学をプログラミングで解く(数学I編)「2-2 三角比の相互関係」』や『高校数学をプログラミングで解く(数学I編)「2-3 三角比の拡張」』で、三角関数の性質③のマイナスの式、三角関数の性質④と同等の式について成り立っていることを確かめました。ここでは、その他の三角関数の性質について、いくつか確かめてみます。
では、順にプログラムを書いて確かめていきます。
三角関数の性質①
まず、
$$
\sin(\theta+2n\pi) = \sin \theta
$$
を見ていきます。
// 三角関数の性質① sin(θ+2nπ)=sinθ の確認
void setup(){
int n = 1; // 任意の整数
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = sin( radians(theta + 360.0 * n ) );
rhs = sin( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード1 三角関数の性質①を確かめるプログラム
ソースコード1を、Processingの開発環境ウィンドウを開いて(スケッチ名を「n360_sin」としています)、テキストエディタ部分に書いて実行します。

図1のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\sin(\theta+2n\pi)}$$)の値、右辺($${\sin \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。今回は$${n=1}$$としていますので、出力は以下のようになります。
10.0 0.17364831 0.17364818
20.0 0.34202024 0.34202012
30.0 0.50000006 0.5
40.0 0.64278764 0.6427876
50.0 0.76604444 0.76604444
60.0 0.8660254 0.86602545
70.0 0.9396926 0.9396926
80.0 0.9848077 0.9848077
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
\sin(\theta+2n\pi) = \sin \theta
$$
は成り立っているだろうということが確認できます。
同様にして、
$$
\cos(\theta+2n\pi) = \cos \theta
$$
や
$$
\tan(\theta+n\pi) = \tan \theta
$$
についても成り立っているだろうということが確認できますので、一度プログラミングしておいてください。
三角関数の性質②
次に、
$$
\sin(-\theta) = -\sin \theta
$$
を見ていきます。
// 三角関数の性質② sin(-θ)=-sinθ の確認
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = sin( -radians(theta) );
rhs = -sin( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード2 三角関数の性質②を確かめるプログラム
ソースコード2を、Processingの開発環境ウィンドウを開いて(スケッチ名を「minus_sin」としています)、テキストエディタ部分に書いて実行します。

図2のように、コンソールに左辺($${\sin(-\theta)}$$)の値、右辺($${-\sin \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。
10.0 -0.17364818 -0.17364818
20.0 -0.34202012 -0.34202012
30.0 -0.5 -0.5
40.0 -0.6427876 -0.6427876
50.0 -0.76604444 -0.76604444
60.0 -0.86602545 -0.86602545
70.0 -0.9396926 -0.9396926
80.0 -0.9848077 -0.9848077
この結果を見ると、左辺の値と右辺の値は一致していることがわかります。つまり、
$$
\sin(-\theta) = -\sin \theta
$$
は成り立っているだろうということが確認できます。
同様にして、
$$
\cos(-\theta) = \cos \theta
$$
や
$$
\tan(-\theta) = -\tan \theta
$$
についても成り立っているだろうということが確認できます。
三角関数の性質③
最後に、
$$
\sin(\pi + \theta) = - \sin \theta
$$
を見ていきます。
// 三角関数の性質③ sin(π+θ)=-sinθ の確認
void setup(){
float theta; // 角度(°)
float lhs, rhs; // 左辺と右辺の値
for(int i=1; i<=8; i++){ // 10°から80°まで動かす
theta = 10.0 * i;
lhs = sin( radians(180.0 + theta) );
rhs = -sin( radians(theta) );
println( theta, lhs, rhs );
}
}ソースコード3 三角関数の性質③を確かめるプログラム
ソースコード3を、Processingの開発環境ウィンドウを開いて(スケッチ名を「plus180_sin」としています)、テキストエディタ部分に書いて実行します。

図3のように、コンソールに角度($${\theta}$$)の値(単位は「°」)、左辺($${\sin(\pi + \theta)}$$)の値、右辺($${- \sin \theta}$$)の値、の順で$${\theta}$$の値を$${10^{\circ}}$$から$${80^{\circ}}$$まで$${10^{\circ}}$$ずつの間隔で出力しています。
10.0 -0.17364822 -0.17364818
20.0 -0.34202015 -0.34202012
30.0 -0.49999997 -0.5
40.0 -0.6427876 -0.6427876
50.0 -0.76604456 -0.76604444
60.0 -0.86602545 -0.86602545
70.0 -0.9396927 -0.9396926
80.0 -0.9848078 -0.9848077
この結果を見ると、左辺の値と右辺の値は丸め誤差の範囲内で一致していることがわかります。つまり、
$$
\sin(\pi+\theta) = -\sin \theta
$$
は成り立っているだろうということが確認できます。
同様にして、
$$
\cos(\pi+\theta) = -\cos \theta
$$
や
$$
\tan(\pi+\theta) = \tan \theta
$$
についても成り立っているだろうということが確認できます。
まとめ
今回は、数学IIで学ぶ「三角関数の性質」について、三角関数の性質についてそれらが成り立っているかどうかを確かめるプログラムを作成しました。
今回は、$${\sin}$$関数のみを確かめてみましたが、$${\cos}$$関数や$${\tan}$$関数についても一度プログラミングしてみてください。
また、今回行わなった三角関数の性質の証明も一度行っておくと勉強になると思います。こちらも是非チャレンジしてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学II(数研出版、ISBN9784410209369)
この記事が気に入ったらサポートをしてみませんか?
