中学数学で扱う未知数 $${x,y}$$ が ”=” を伴って出現するのは、17世紀、最初の産業革命より後のことであり、結構最近のことである。デカルトが”座標” の概念を導入するまで、直線も放物線も $${x,y}$$ で表されることはなかった。
一方で、数学自体の歴史は圧倒的に古く、中学数学の最後に学習する「三平方の定理」、すなわち「ピタゴラスの定理」は遅くとも紀元前6世紀には発見されている。コンパスの代わりに縄を使った「作図」は紀元前3000年の古代エジプト文明の土地の測量で盛んに使われており、「数字」もその前には発見されている。それでは $${x,y}$$ も "=" もない時代、人々はどうやって数学していたんだろうか。

x, y がない数学の姿

デカルト以前から方程式はあったが、長い間
『ある辺の2乗は、その辺の2倍の長さに1の長さの辺をかけたものに等しい（ $${x^2=2x×1}$$ ）』
などといった自然言語で記述されていた。”＝”がないため、この時代は式を移項するたびに「○○は、××と等しい」と毎回書いていたらしい。これは相当めんどくさい。

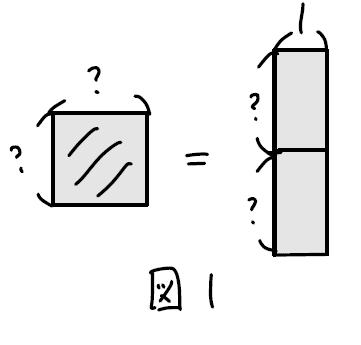
ここで中学数学に慣れた人は、なぜ「$${2x}$$」を 「その辺の2倍の長さに１の長さの辺をかけたもの$${2x×1}$$」として、わざわざ1をかけているのか、疑問に思うのではないだろうか。しかし、デカルト以前の人にとって、この 1の長さの辺 は必須だった。この方程式を書いている人の見ている景色は、図1のように2つの「面積」なのである。

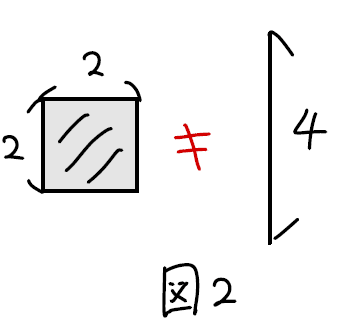
この時代の方程式は、左辺と右辺の「量」だけでなく「意味」まで同じものを指す必要があった。ある量を2乗したら、それは図形で言えば「面積」である。「面積」と等しいものは「辺の長さ」ではなく「長さ×長さ」の「面積」でないといけない。下の図2は数字は一緒でも「等しくない」のだ。1の長さの辺が必要だったのは、面積にして意味を揃えるためにある。ここで強調することは、16世紀までの方程式には「イメージ」が伴っていたという事実である。

便利さを優先すると、”意味”が消える。

デカルトより少し前に、数学の主な担い手は、王族や貴族から、イタリアの商人の手に移る。商人にとって大事なのは「意味」ではなく「素早く計算できる」ことである。彼らの手によって、０を表す記号を持たないローマ数字から、インド・アラビア数字に切り替えられ、$${A, B,x,y}$$などの記号が導入された。イタリアの算術教師の一人、ロバート・レコードは自身の著書『知識の砥石』の中で、200回以上「～～は等しい」という言葉を使って、ふと "=" という記号を導入すれば、長ったらしい言葉の繰り返しを避けることができることに気づいたという。

商人たちの尽力のおかげで17世紀には、ようやく$${x^2=2x×1}$$ とかけるようになった。最後に残った ×1 はデカルトが「1をかけて必ず調整できるのなら、計算する上では式に残しておく必要はない」と気付き、次元を撤廃する。こうして方程式は ”意味” から解放され、"イメージ"を持たないものとなった。

"イメージ"を復活させるために。

話を現代に戻そう。
僕たちが学校で習っている数学は、計算しやすいように記号化した後の数学だ。しかし扱っている題材自体は、「ピタゴラスの定理」など紀元前の産物であり、近代より前の”イメージ”があった頃の数学だ。 学校で習っている数学は ”イメージ” が伴っていた数学を記号化して、意味が見えずらくなった代わりに機械的に操作しやすくしたものである。つまり、学校でやっている数学の操作に対応するイメージは必ずある。だから、こう言い切ってみる。

イメージができないまま、数学をする必要はない

意味がない操作の組み合わせに見える方程式を解くという行為にさえ、イメージは伴っていたのだ。もし、学校で習った数学の何かを理解できないときは、たぶんイメージができていない。移項が分からなかったら、移項するときに頭のイメージを操作している 同級生に聞いてみよう。
ここで「なぜ、そうする（とうまくいく）のか」を聞いても、その人のイメージは見えてこない。聞くべきことは「なぜ ”そうしようと思った” のか」だ。

移項なら
「なぜ引いて0にしようと思ったのか」、

他の問題なら
「なぜそれを $${x}$$ と置いたのか」
「なぜその補助線を引こうと思ったのか」、
「なぜその三角形から考えたのか」、

正しさではなく、数学で何かを操作しようとする気持ち、衝動の方を捉えることで、見えてくる景色がある。補助線が引ける人は、そこに何かイメージが見えている。もし数学に ”センス” というものがあるならば、僕はそのイメージの豊かさを指しているように思う。

音楽をする人にとって、「気持ちいい」音と「気持ちよくない」音があるようだ。この感覚を音階などで論理的に説明できたとしても、最初にあるのは音に慣れ親しんで感覚が鋭くなった人の持つ「景色」だと思う。音楽をするのに最初に必要なのは、「こんな音を出せたら、気持ちいいだろう」という気持ちだ。数学も、同じように「気持ち良い」数学を探してみたら、面白く感じれるのかもしれない。