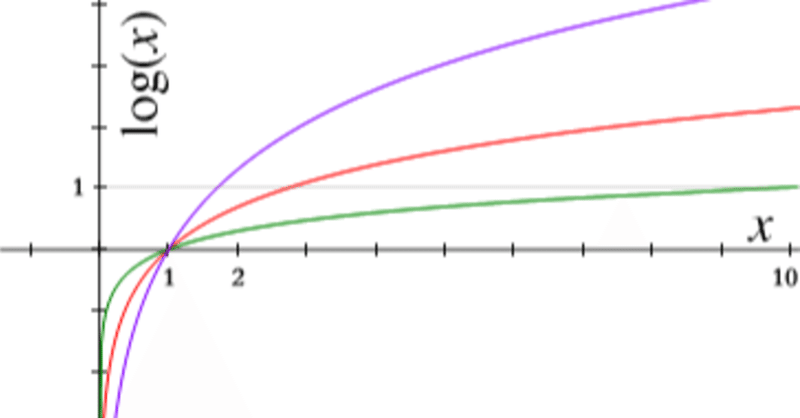
【高校数学】logを使って???桁数を求める???
皆さんこんにちは!
日常の中で様々なことに疑問を持ち、学んでいっているのですが、せっかくなのでそれを発信していき、共有していこうと思っている、そんな企画でございます。
今回は数学Ⅱ常用対数を用いてでかい数の桁数を調べたり、小さい数の最初に数字が出てくる場所を調べたりするあれです。
指数対数のイメージ
数学Ⅱの教科書を開きます。
式と証明
複素数
図形と方程式
三角関数
指数関数・対数関数
微分積分
目次にはこの教科書で扱っている分野が網羅されていてワクワクしますね!(人によっては胃がキリキリでしょうか?)
普通は最初のページから最後のページに向けて授業を行います。
数学が苦手な人に配慮しながらゆっくり進め、ピーチクパーチクどーでもいいことをしゃべってくる生徒をいなしながら、ワーワー騒いでるやつに「うるせー!」って言って、授業と全然関係のない過去の自分の武勇伝をどや顔で語って・・・
気づくと12月、1月。もうそろそろ3年生です。
「しまった!教科書全然進んでないではないか!!」
そう焦った先生はやっとペースを上げてきます。
蔑ろにされる指数対数・・・
こんなんじゃありませんでしたか?
僕の高校時代はこうでした。
高校数学のゴールは数学Ⅲの微分積分です。
この微分積分をするために2年間必死こいて基礎を学んでいくわけです。
そんな重要な微分積分の分野を捨てるわけにはいかないので、消去法で指数対数の方が切られるんですね。
とはいえ、指数関数・対数関数の微分積分も行うので、関数としての性質と指数・対数の計算方法はやっておかないとねぇ・・・
そうなったとき、白羽の矢が立てられるのが"常用対数の利用"なのです。(多分
ここまでの文は本文と何の関係もありません。
すみません。
以下本文です。
ドマイナーな問題
そんな指数対数分野における常用対数の問題
「○は何桁の整数か答えよ。」
「○は小数第何位で初めて0でない数が現れるか答えよ。」
これまで散々方程式とか解かされてたのにここにきて小学生みたいな・・・
って感じましたよね。
しかも「常用対数表」とかいう教科書の付録を使わされます。
「俺の知ってる本の付録ってエコバッグとかだよ!!」
と泣きながら突っ込んでる皆さんの顔が浮かびます。
結局よくわからないまま時が進んだ方も多いと思いますので、
今回の記事ではここを重点的に解説していきたいと思います。
対数ってなんやねん
んでまぁ
そもそも対数とはって話なのですが、
結論から言っちゃうと指数関数の逆関数ですよね
逆関数ってちょっと裏ルートみたいなイメージが僕にはあるのですが、
三角関数の逆関数、アークサインとかは高校ではやりません。
それなのに指数関数の逆関数はちゃんと勉強するってなんだか不思議な感じもします。
ここら辺は恐らく、微積分をするときに対数を使わないと解けない問題だったり、対数を使うことで遥かにわかりやすくなる問題だったりがあるからかとは思いますが。
とはいえ、本来の対数はこんな深い話ではなく、指数を見やすくするところから始まったのです。(デデン!
ちなみに、対数って数学で出てくる「こんなの何に使うんやねん」数式の中でもトップクラスに役立っているのでこういう話が好きな先生とかは積極的に説明してくれているかもですね。
対数伝説の始まり
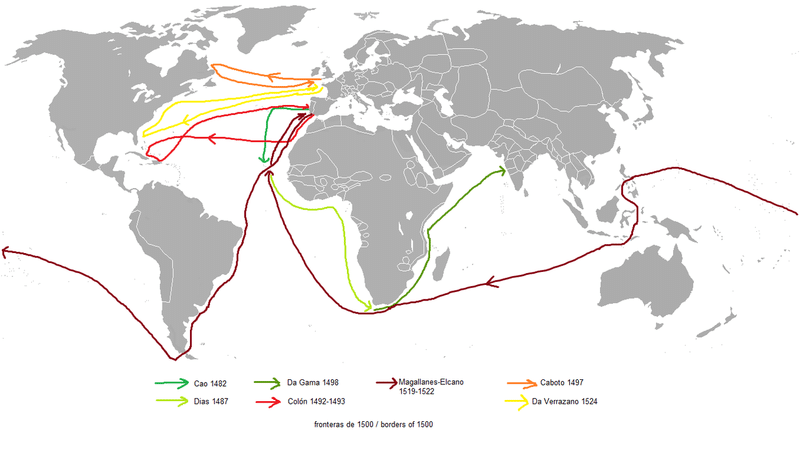
ー時は17世紀。大航海時代真っ只中。ー
欧米各国は新天地を求め大海原へ駆け出しています。
日の沈まない国スペイン、ポルトガルの後を追うようにイギリス、フランス、イタリア、オランダたちが次々と船を出しました。
ここで考えてみてほしいのですが、
彼らはどうやって目的地にたどり着いたのでしょうか?
今の我々の感覚で行くと、
「グーグルマップ開いて、GPSで現在地と目的地を調べて~」
「電波届かないところ行っちゃったらやだなー。せめて3Gくらいの速度は欲しい・・・」
なんて呑気なことを考えるかもしれませんが、当時はスマホなんてないですよ。
じゃぁどうやって航海をしたのかというと、計算したんですね。
当たり前だけど。
具体的な計算方法は分かりませんが、地平線から太陽の角度、時刻、影の付き方、方位磁石とかを使って自分の位置を計測したんだと思うのですが、
複雑な三角関数を使う上に、地球規模の計算。
桁数が莫大な計算。
238928×39928
なんて誰もやりたくないでしょ!?
角度が1度ずれても数百キロ進めば誤差はえげつないことになるので、絶対にミスは許されません。
実際に何人もの航海士が遭難をしたそうです。
まさに命がけの計算・・・
そんな超疲れる計算をはるかに楽にできるような方法を見つけた人がネイピア男爵

ジョン・ネイピア(1550-1617)
ちょっと計算しただけで莫大な数になる掛け算を足し算に変換し、超細かい小数点が出てくる割り算を引き算に変換するという「小学生の時に教えてくれよ!」な発明品を開発します。
そしてこの手法のことを「ロガリズム」と名付けました。
是非、対数の授業の時に「あぁーロガリズムねー」ってどや顔で言ってみてください!めっちゃウザがられます!
余談ですが、ネイピア男爵、なんとシェイクスピアと同世代の偉人なんですね。
やはり余暇はシェイクスピアの作品を鑑賞していたのかしら・・・
妄想が膨らみますね。
大きな桁になれば大きな桁になるほど対数の重要性が増してきます。
50万円の車に保険かけるよりも2000万円の車に保険かける方が安心感があるみたいなもんです。
このこともあって、「ネイピアは天文学者の寿命を倍にした」なんてよく言われていますね。
宇宙規模になるとその桁数は桁違いになるので(けただけに)
対数の仕組み
じゃぁその対数ってなによって話ですが。
簡単に言ってしまえば、
数自体を見るのではなく、桁数を見る
という考え方をします。
100を百ではなく「ゼロが2個」
10000000を一千万ではなく「ゼロが7個」
みたいな感じですね。
そうすると、100×10000000は
ゼロが2個+ゼロが7個=ゼロが9個
という誰でも暗算できるような足し算に変換されるのです。
てかこれ、みなさんも小学生の時にやってたでしょ?
「×100は後ろにゼロを2個足すんだよー」って
あれって対数的な考え方だったんですね。
んでまぁそもそも莫大な数って指数なわけで、
その莫大な指数を目に見える小さな数に落とし込んでやるから指数関数の逆関数になるんですね。(多分ちょっと違う
ここで大事なのは
恐ろしく大きい数を手に負える数まで小さくできる
という部分です。
恐ろしく大きい数を紙に書くのには指数を使えばいいのですが、それを計算しろって言われると指数だけだとちょっと不便だったんですね。
紙に書き記せないほど大きな数を
「どれくらい大きいのか」に注目して目に見える形にするというわけです。
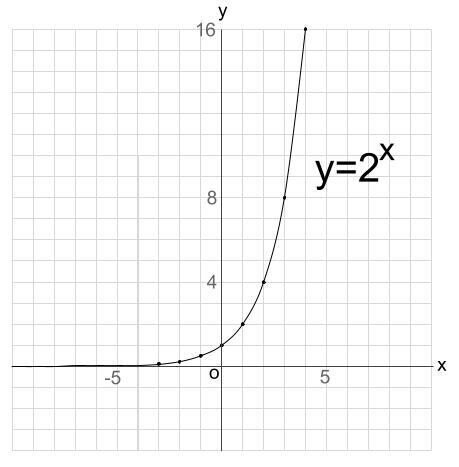
指数関数のグラフはx=4くらいで紙からはみ出てしまいます。
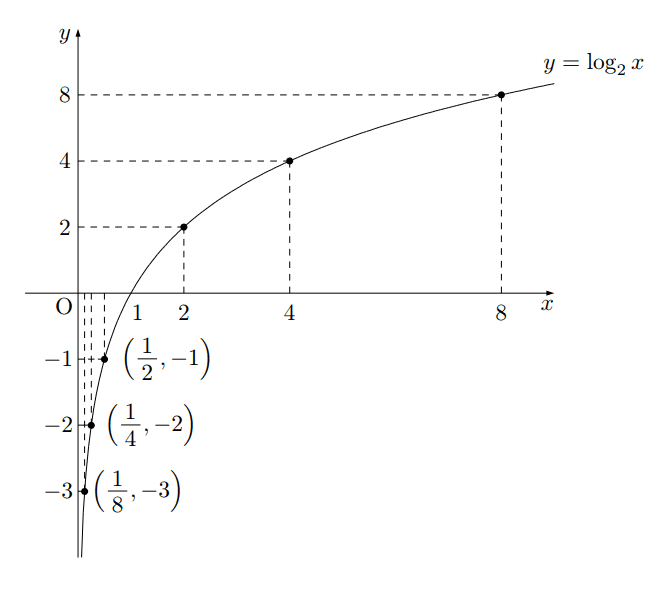
その点、対数関数のグラフは大分緩やかなカーブになってくれています。
これならしばらくは考え続けられそうだ。
大きな数の桁数を調べる
そんな功績を残したネイピア男爵ですが、現代となってはコンピュータが複雑な計算をいくらでもこなしてくれます。
もはや過去の産物となってしまった常用対数…
それを少しでも活躍させてあげようとしているのか、教科書では桁数を調べる問題が出されます。
ちなみに、
桁数をまとめ上げる常用対数はお役御免になりつつありますが、
極限(微分)と相性を良くした自然対数はこの世の真理を追い求めるために今でも重宝されています。
「微分しても数が変わらない」という、あまりにも都合がよすぎる数、ネイピア数が見つけられたためですね。
すげーぜ、ロガリズム!
そこで、まず「桁とは何か」を改めて考える必要があるのですが、
そこに関しては、以前書いた「n進法」に関する記事で説明しています。
ちょっと覗いてみてください。(宣伝
桁というのは「ゼロが何個付くか」であり、
そのゼロは10のべき乗ごとに増えていきます。
10のn乗の数は(n+1)桁です。
んで、その「0が何個付いているのか」を言っているのが対数logなのです。
ここでは「10」進法で考えるので、
![]()
と、底は10になっています。
恐らく2進法だと底は2なんじゃないですかね?
皆さんの前にバカでかい数字がやって来たとしましょう。
バカでかすぎてもはやどのくらいでかいかすらもわかりません。
その身長は雲を突き抜け、月まで届くほどなのではないでしょうか。
そこへ「対数」を名乗る男がやってきます。
「俺に任せな・・・桁を教えてやるぜ・・・」
つまりはそういうことなんです!
例)
![]()
ちなみに、2の8乗って256です。
今回は答えが合っているのかすぐわかるようにわざわざ対数使わなくてもわかるような小さい数で例題を解いてみます。
まずはこのバカでかい数字を目に見える形まで落とすために対数を取ります。
![]()
自然対数は数字に戻しましょう。
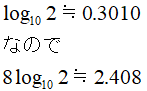
ってことは次のことが分かりますね。
![]()
で、さっき言ったように、logってのは0が何個付いているかを表しています。
なので、今回の場合は0が2.408…個くっついているので、
100って感じで3桁の数だって分かりますね。
実際に256は3桁の数字です。
トップを調べる
これ、もうひと手間加えるとバカでかい数字の一番先頭の数まで調べられるらしいんですよ。
何に使うんだって感じですよね!
まぁ実際に7億なのか9億なのかで誤差が2億もあるので、トップの数字が分かるだけでも大分その数字の全体像がつかめます。
時と場合によってはとても重要な技術なのではないでしょうか。
僕は今まで一度も使ったことありませんが。
例)
![]()
今回も答えが256だとわかっている2の8乗を例にしてみます。
もちろん答えは「2」です。
で、具体的にどうするかって話なのですが、
とりあえずトップの数をpとでも置いてみましょうか。
200だったらp=2だし、300だったらp=3になるわけです。
分からない数字があったら未知数で置け!は数学界の鉄則ですよね。
この数字が3桁ってことは先ほど求めました。
なので、
![]()
ということが分かると思います。
どういうことかというと、
答えは2なのでp=2なわけですが、
200≦256<300
と言いたいってわけです。
厳密にいえば"200以上"ということになりますが、まぁどっちも「より大きい」、「より小さい」って書かれていた方が覚えやすいでしょ。
この関係、式で書きましょう。
![]()
例によって対数を取ります。
基本的に高校レベルの数学の問題で「指数が出てきたら対数を取る」と機械的にやって問題ないですが、「指数がでかすぎて手に負えないので対数の世界で考える」という根本的な部分はちゃんと理解しておくとこれから先、生きていくうえでお得です。
全然関係ないですけど、「この先生きていく」って「このせんせいきていく」って読んじゃいますね。
話を戻します。対数を取ります。
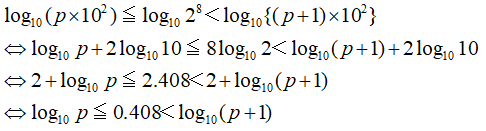
はい。
途中の流れはいろいろと省いていしまいましたが、
logの中の積を和にして、指数を落として、8log2を計算して、各辺から2を引いたのですが、
logの計算自体はこの記事の本質とは違うと思ったのでざっと書いてしまいました。
不評であればしっかりと書きます。
そして、
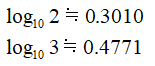
であることを踏まえると、0.408という数値は
![]()
こんな感じでlog2君とlog3君に挟まれていることが分かりますね。
つまり、
![]()
という不等式の
pは2だということがわかります。
そして何を隠そう、このp=2こそが今回求めたかったトップの数字でしたよね!?
つーわけで、2の8乗は3桁の数字で、一番先頭の数字は2!!
こんなことまでわかった!素晴らしい!!
どんどん応用していくぜ!
指数の桁数とトップの数が分かるってことまで学びました。
これ、逆を考えたらどうなりますかね?
人間ってのは常に逆を考えたくなる生き物ですよね?
???
指数がどんどん小さくなっていって「負」になった場合どうなるのか、
気になりませんか?
気になりませんか。
気になってください。
ということで、ここからは指数が負になった場合を考察していきたいのです。が、
皆さん、ここまで読むのに何時間かかりましたか?
編集画面で右上に表示される現在の文字数を見ると、
すでに5000字を超えてるんですよね・・・
僕が疲れたので続きはまた今度にします!!!
↑↑↑↑続き
ということで今回はここまで。
今回の記事がためになったという方、面白かったという方はぜひSNS等でシェアしてくださると嬉しいです。
間違いがあったりしたらコメント等で教えてください。
また、「お疲れ!コーヒーでも飲みな!」という方はサポートをしてくださるととても励みになります!
また、他の記事もぜひ見てみて、ついでにTwitterのフォローもお願いします!!⇒https://twitter.com/mazenemaze
それでは、また次回の記事でお会いしましょう!!
この記事が気に入ったらサポートをしてみませんか?
