
流体力学 縮流係数
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第55回目は,「翼理論」をについて紹介したいと思っていましたが,普段使用している教科書を見返したとき,筆者が興味深いと思った内容に触れるため,「縮流係数」に変更します。
今回は,以前に投稿した「シュワルツ・クリストッフェルの定理」と「シュワルツ・クリストッフェルの定理(その2)」,「シュワルツ・クリストッフェルの定理(その3)」を使った内容となりますので,気になる方は以前の投稿記事もご確認ください。
(1)縮流係数とは
さて,不特定多数の皆様は「縮流係数」(もしくは,収縮係数)をご存知でしょうか。この用語だけを説明すると,「流体の通る管路断面積と管路を狭めた断面積の比」のことをいいます。
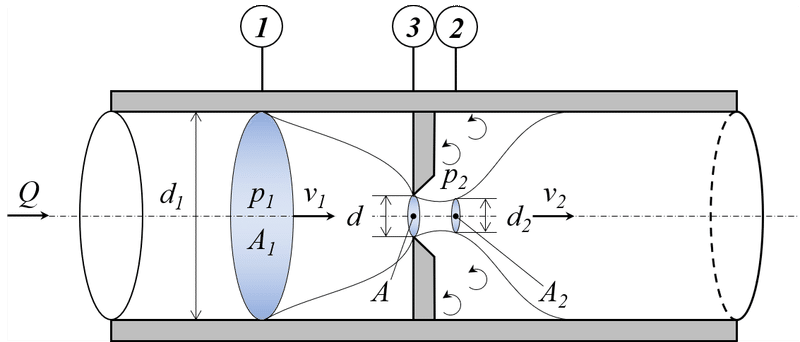
これだけでわかる方は,頭の中にすぐ図が浮かぶ人だけのはずなので,以下に図解したいと思います。図1にオリフィス管内の流れの概念図を示します。ここで出てくるオリフィスとは,比較的薄い板に設けられた孔より流体が噴出するもののことを指します。なぜオリフィスを取り付けるかについては,「管内の流量を測定する」ためです。
今回は,あくまでも「縮流係数」に焦点を当てるため,オリフィスの解説はまたの機会に持ち越したいと思います。
オリフィスは流れに垂直に設置して,中央に直径dの孔をもつとします。断面1はオリフィスを通過する前の管路断面であり,断面2はオリフィスの直径dの孔を通過した後の管路断面です。左から右に流れる流体に注目すると,断面2ではオリフィスの直径dの孔よりも小さくなっています。オリフィス通過後の流体は,管内の外側に剥離していくことから流線(仮想の流体の外形線)は,おおよそ断面2と同じ断面積となることがわかっています。
よって,「縮流係数」の定性的な表現としては「縮流による損失係数」を示し,定量的な評価方法としては「流体の通る管路断面積と管路を狭めた断面積の比」として計算できることを意味しています。
そして,オリフィスの設計では,これまでの多数の実験データから「縮流係数」を計算する実験式なども多くあり,JIS(日本産業規格)でも推奨される計算式があります。(JIS Z 8762-2参照)
設計でよくやる手法として,ざっくりした当たりを付ける計算をすることがあります。そのときの「縮流係数」は「0.64~0.65」として計算するそうです。この根拠となるのは,図2に示すようなオリフィス管内の流れが成立するためと考えられます。

ここで,筆者がずっと気になっていたことをいいます。
なぜ,「縮流係数」は「0.64~0.65」として計算してよいのか。
筆者としては,偶然の産物に対して,適当な値を当てはめただけと思っていました。感覚的には,水のような非粘性流体では問題なくとも,油のような粘性流体ではオリフィスの直径の孔を小さくし過ぎると,確実に詰まることが想像できます。しかし,オリフィスもJIS等で規格化されている以上,定量的な評価ができているからとある直径の孔(0.8d)より小さくならないのではと思っていました。
以上のような疑問を抱いていた筆者でしたが,この問題は解決されていました。実は,「縮流係数」の定量的な評価が「可能」でした。それも,以前に取り組んだ「シュワルツ・クリストッフェルの定理」(以下,SCの変換式)を使うと求まることに…。
今回の目標は「縮流係数の最小値」を求めることです。
(2)縮流係数の最小値
では,縮流係数の最小値を求めることにしましょう。今回の解答はかなり長くなるので,計算結果だけ知りたい人は,(3)縮流係数の結果だけをご覧ください。
(問)
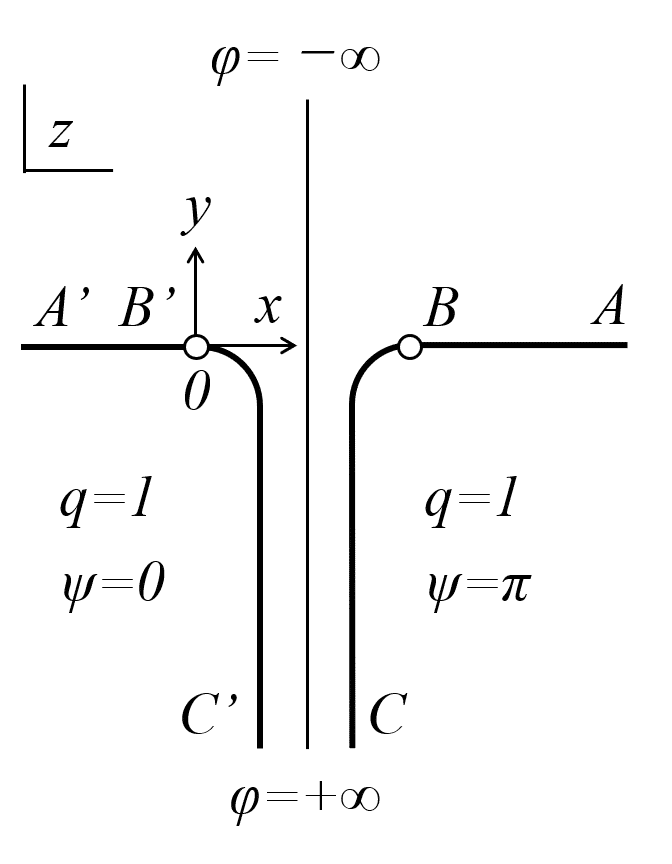
図3のz平面に示すように,器の平らな底に開けた孔から流体が落下する場合の自由流線B’C’の形状ならびに孔の幅B’Bに対する無限遠におけるC’Cの比,すなわち縮流係数を求めよ。(z平面の流線形状はかなりトリッキーな形をしていますが,図3のような形が与えられると考えましょう)
(解)
まずは,z平面の肉付けから始めます。z平面のy軸は,流れの速度ポテンシャルが増すため,y軸下向きを正として,φ=+∞と設定します。逆に,y軸上向きを負として,φ=-∞と設定します。さらに,点B’,点Bの流線ψの値をそれぞれψ2=0,ψ3=πになるように設定します。
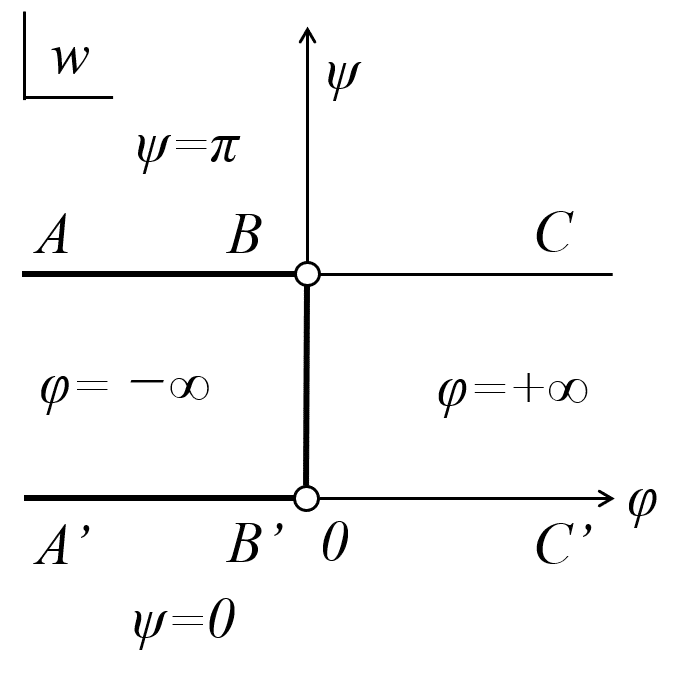
次に,z平面からw平面に変換します。先ほどの設定した点A’,点B’,点B,点Aの各点は,ψ1=-∞,ψ2=0,ψ3=π,ψ4=+∞となり,図4のようなw平面となります。このw平面は,複素数w=φ+iψにより図4のように無限長の帯状領域となります。
次に,w平面からζ平面の上半面に変換します。
まずは,「定理を使うときの注意事項1」の「点A’,点B’,点Bに対してξ1,ξ2,ξ3の3つは任意に選べるものとする」を使います。今回は,ξ1=-∞,ξ2=-1,ξ3=1を選択します。また,点Aは無限大に発散するため,それに対応するξ4=+∞とすることが出来ます。これにより,図5のようなζ平面となります。
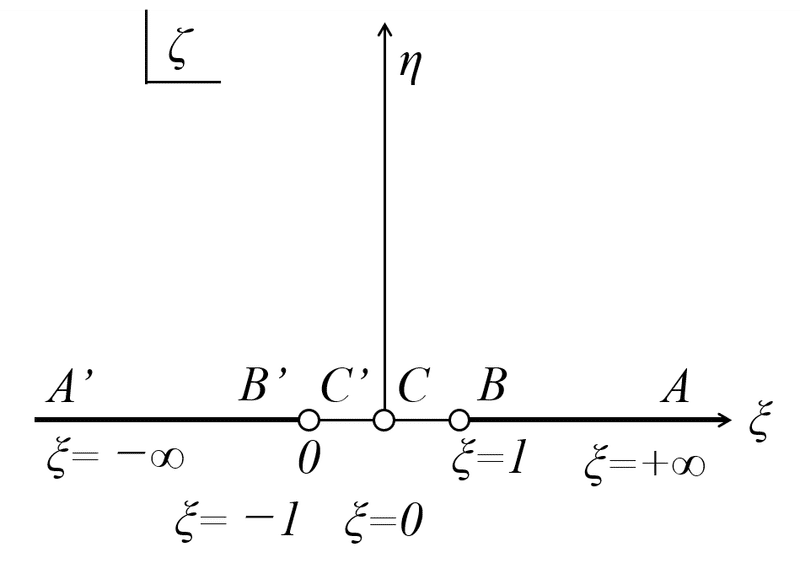
以下に,ζ平面におけるSCの変換式から微分方程式の一般解を求めた結果を示します。
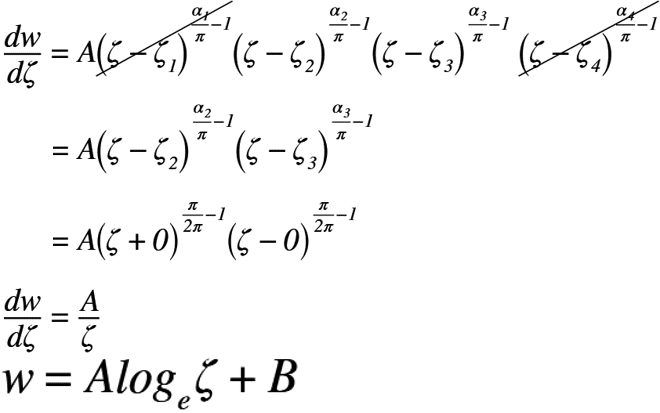
ここで,境界条件:ζ=ξ=1のとき,w=iπの条件を一般解に代入すると,以下のようになります。
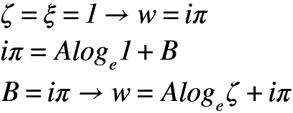
ここで,境界条件:ζ=ξ=-1のとき,w=0の条件を一般解に代入すると,以下のようになります。
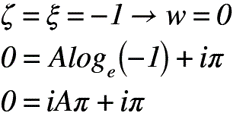
よって,定数A,Bの結果を一般解に代入すると,特殊解(式(1))は以下のようになります。
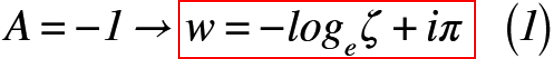
ちなみに,上式の結果は以前に投稿した「シュワルツ・クリストッフェルの定理(その3)」の問題でも取り上げたものと同様です。
次に,共役複素速度dw/dz = u-iv = q(cosθ-isinθ) = qe^-iθとすれば,式(2)のようになります。分母分子がひっくり返っているので,注意しましょう。但し,任意の速度の大きさq,x軸とのなす角θとします。
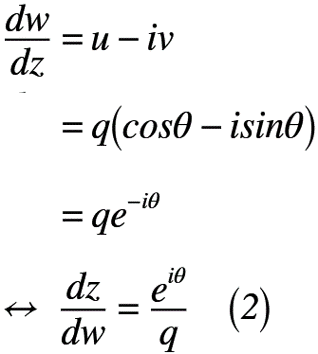
最後に,Ω平面に変換するため,Ω平面の対数速度Ωは,式(3)のようになります。
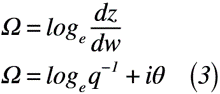
ポイントは,図3のz平面の原点を「点B’」としたことです。これにより,A‘B’は角度θ=0に沿って, ABは角度θ=-πに沿うことになります。速度の大きさqは,角度θが変化するものの自由流線B‘C’とBC上で一定値となります。
つまり,速度の大きさq=1とすることで,自由流線B‘C’とBCは虚数軸上に存在することになり,Ω平面の半無限長の帯状領域となり,図6のようになります。これで平面の変換作業は終了です。
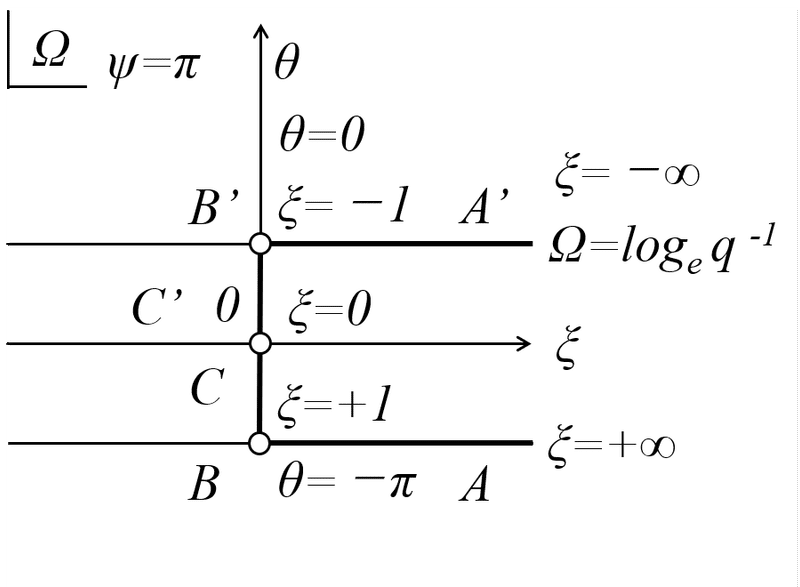
ここで,先ほどのw平面からζ平面にSCの変換式を使ったのと同様に,ζ平面からΩ平面にもSC変換を適用します。
以下に,Ω平面におけるSCの変換式から微分方程式の一般解を求めた結果を示します。
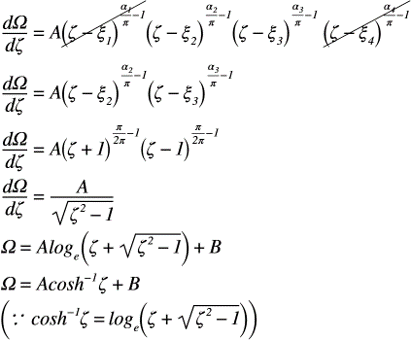
ここで,境界条件:ζ=ξ=1のとき,Ω=-iπの条件を一般解に代入すると,以下のようになります。

ここで,境界条件:ζ=ξ=-1のとき,Ω=0の条件を一般解に代入すると,以下のようになります。
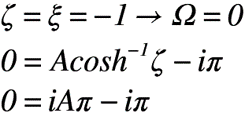
よって,定数A,Bの結果を一般解に代入すると,特殊解(式(4))は以下のようになります。
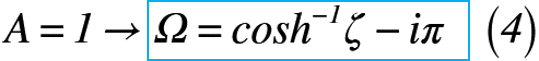
次に目指すべきは,複素数z=x+iyの各座標を求めたいのです。
図3のz平面を確認すると,B’BとC’Cの長さを求めたいので,点B‘を原点に置いていることを利用すれば,各点までの距離がx,y座標が求まることで分かります。
そのため,変換を繰り返してきたΩ平面(ξθ軸),ζ平面(ξη軸),w平面(φψ軸),z平面(xy軸)の関係式を解いていく必要があります。
そこで,式(3)を特殊解(式(4))に代入すると,式(5)のようになります。
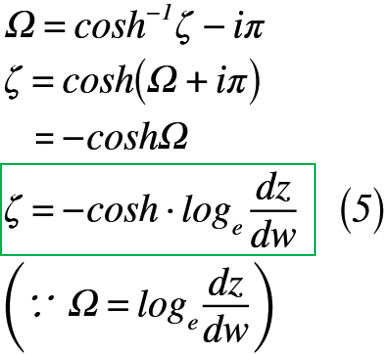
上記の式(5)は,ζ平面からΩ平面にSC変換したものです。もう一つは,w平面からζ平面が残っているので,式(1)を変形してみると,式(6)のようになります。
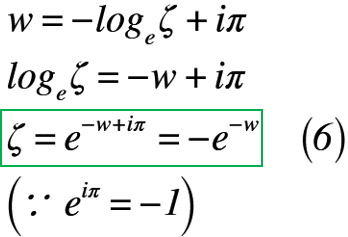
ここで,ζが式(5)と式(6)と等しいことを利用すると,以下のようになります。
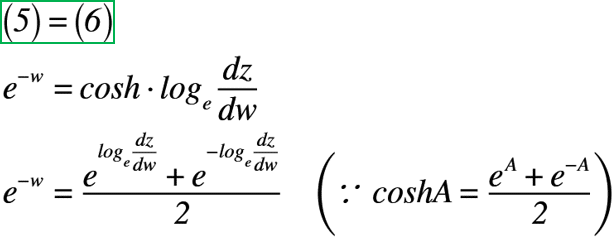
これ以上は計算できないように感じますが,式(3)を上式に代入すると,以下のような(dz/dw)の2次方程式が得られます。
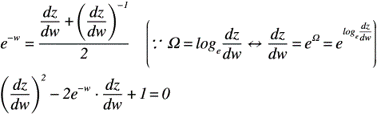
上記の2次方程式は,因数分解して解けるパターンではないため,2次方程式の解の公式を使うと,(dz/dw)の解が得られます。
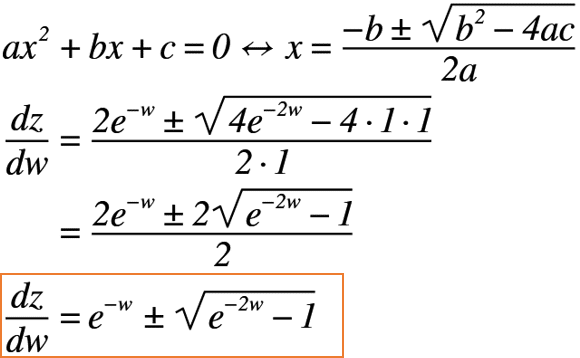
以上より,2次方程式の解が算出できた訳ですが,これではまだ不十分です。なぜなら,解が「2つ」あるからです。可能なら「1つ」に絞りたいですよね。そのためには,(dz/dw)の解が+になるか,-になるかを確かめればよいのです。
ここで,ψ=0,φ=-∞となる場合について各平面で考えます。このとき,z平面では点A’が最も近くなり,速度の大きさq=0となります。同じく,Ω平面ではq=0になることからθ=0となり,共役複素速度(dw/dz)の極限を考えると,以下のように+∞となり,+の領域のみを考慮すればよいことになります。
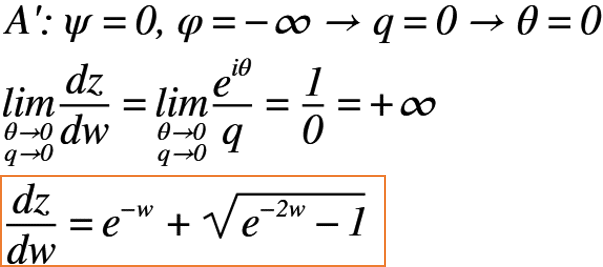
つまり,前述した2次方程式の(dz/dw)の解は,以下のように+の領域を考慮した1つの解となります。
次は,複素数zにしたいので,上記の(dz/dw)をwについて積分すると,以下のように求まります。不定積分の計算であるため,積分範囲の指定は必要ありませんが,置換積分の計算は必要となります。

以上より,zの一般解が求められました。次の作業は,上記の一般解を特殊解にするために境界条件を当てはめます。
ここで,点B‘の境界条件:z=0→w=0(z平面とw平面)を一般解に代入すると,積分定数Cは以下のように求められます。
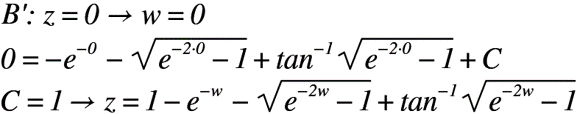
次に,自由流線B’C’の境界条件;ψ=0(z平面)をw平面の複素数wに代入すると,以下のようになります。
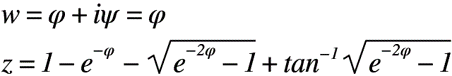
上記の結果と定数Cを一般解に代入すると,複素数zの特殊解が得られます。
ここで,複素数zの中身をより計算しやすいように式変形します。(正直なところ,これを思いつく暇人はマジですごいと思います)
具体的には,自由流線B’C’に注目します。この流線φは,点B‘ではφ=0,点C‘ではφ=+∞となり,流線φの存在範囲は,0<φ<∞となります。この存在範囲を複素数zの平方根の中に利用すると,以下のように式変形ができます。
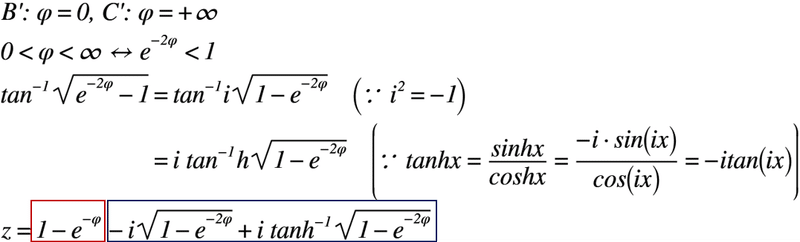
上記の結果を複素数zの特殊解に適用すると,三角関数,双曲線関数の関係から以下のように書き換えができます。
上式は,複素数z=x+iyなので,実軸xと虚軸yにそれぞれ比較すると,式(7)のようになります。
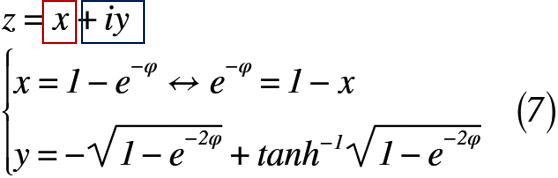
でもこれで終わりではありません。なぜならば,w平面の実軸φが残っていると,今後の議論が進められないからです。そのため,式(7)のφを消去するために,以下のように実軸xを式変形します。
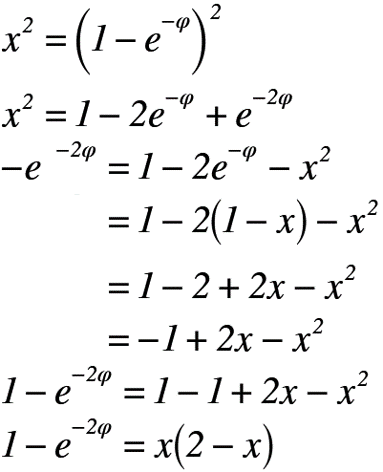
式変形によって得られた実軸xを虚軸yに代入すると,以下のようにxとyの関数に持ち込めました。この式こそ,z平面における「器の平らな底に開けた孔から流体が落下する場合の自由流線B’C’の形状」を示す式となり,題意の1つ目をようやくクリアしました。
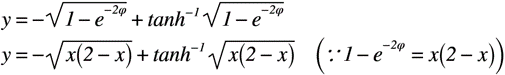
ここまで求まれば,最後の仕上げです。まずは,無限遠におけるC’Cを求めます。そこで,無限遠における点C’のx座標は,極限を考えると,以下のようになります。
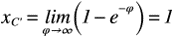
この結果を利用して,無限遠におけるC’Cを算出します。C’Cの距離は,流線であることを利用すると,流量と流れ関数の関係式を使って,以下のように説明ができます。この関係式は,以前に取り上げた記事をご参照ください。そして,z平面の点C’と点Cのψの値を確認すると,流れ関数ψは2通りの記述ができます。
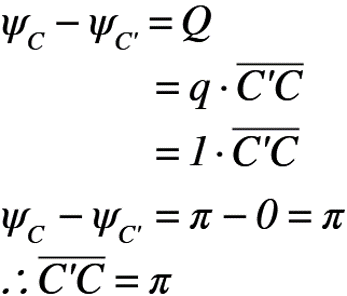
よって,無限遠におけるC’Cの距離は「π」であることがわかりました。
次に,孔の幅B’Bを求めます。これは,図3のz平面を見ればわかります。
無限遠における点C’のx座標は原点B’からの移動量を示しています。つまり,B’C‘の長さはxc’となり,前述した無限遠におけるC’Cの距離も分かります。さらに,BCの長さは,z平面がy軸に対称な自由流線が描かれていることからxc’となります。
したがって,2つ目の題意である「孔の幅B’Bに対する無限遠におけるC’Cの比(縮流係数)」は以下のように求まります。
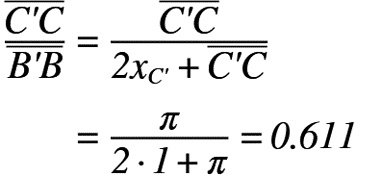
長い道のりでしたが,以上の結果から縮流係数は「0.611」程度になることがわかりました。
(3)縮流係数の結果
さて,最後は前項で得られた縮流係数が「0.611」の結果を使って,オリフィスの直径の孔をどのくらいに設定すればよいかを見ていきましょう。
前述の通り,縮流係数は「流体の通る管路断面積と管路を狭めた断面積の比」で計算されます。そのため,管路断面積の直径d,管路を狭めた断面積(オリフィス)の直径dc,縮流係数Cc=0.611として計算すると,以下のように直径dcが求まります。]
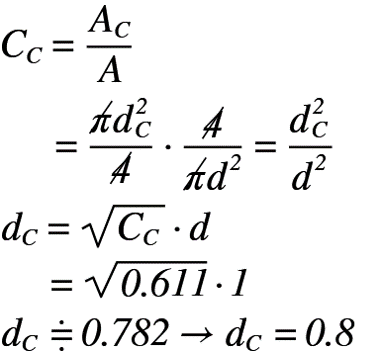
この結果,オリフィスの直径と管路断面積の直径の比は,以下のようになり,オリフィスの直径dcは0.8倍となることがわかりました。
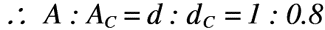
つまり,JISで規格化されているオリフィスの直径は,きちんと考えられたものであるのです。
以上の結果からわかる通り,こんなにも長い道のりを経て,縮流係数は算出されているのです。筆者の疑問は,思ったよりもヘビーな内容で驚きました。これを大学・高専での講義で伝えるのは,間違いなく不可能です。今後の参考になれば幸いです。
(4)まとめ
今回の記事のまとめを以下に示します。
① 縮流係数は,縮流による損失係数であり,流体の通る管路断面積と管路を狭めた断面積の比として計算する。
② 縮流係数の最小値は,SCの変換式を用いた計算によると0.611となる。
③ 求めた縮流係数の最小値からオリフィスの直径の孔は,0.8となる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「翼理論」について,解説する予定です。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
