皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第８回目は，第７回目でネタにした「複素ポテンシャル」の補足についてかいていきたいと思います。前回の「複素ポテンシャル」をまだご覧になっていない方は，以下の記事を見てみてください。
※今回の記事は，かなり数学的な説明が多いため，数式が羅列することになることを予めお伝えしておきます。

（１）スルーしてはいけない記事の一文

　完全に前回の「複素ポテンシャル」を知っている人，あるいは記事を見て頂いた方に限定してしまい，大変申し訳ございません。ですが，あの記事でスルーしていけない一文が２カ所もあるのです！今回は，その1つ目を取り上げます。
　では，その一文とはどこなのでしょうか？
　以下に答えとなる一文を示します！

「ここで，式（２）の必要十分条件が成立する場合は，コーシー・リーマンの微分方程式の式（３）が成立します。」

　但し，上記の式（２）については，実関数w＝複素関数w(z)を示しています。この一文で「おいおい！」とか，「ちょっと待った！」と思った人は，「良く気づきましたね！」と一言を送ります（笑）。

　実は，ここでスルーしてはいけないのは，「実関数w＝複素関数w(z)の必要十分条件って何よ？」なのです。
　さも当たり前のように言っているのですが，全然当たり前ではありません！これは，以前に取り扱った「コーシー・リーマンの微分方程式」と同様に高校数学の「命題と命題」の出番がまたもや来てしまいました。
　では，図1に実関数と複素関数の命題関係を示します。

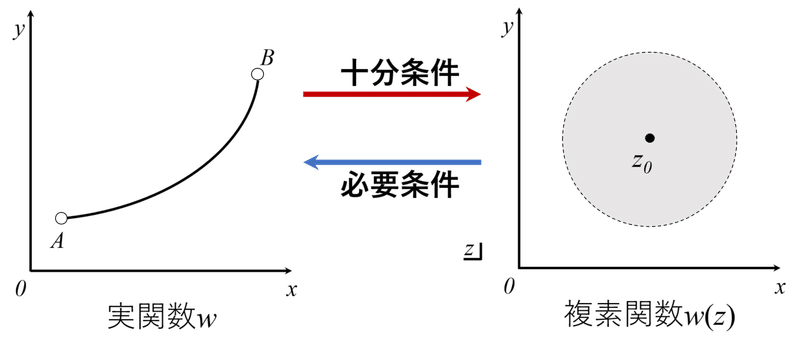
図１　実関数と複素関数の命題関係

　ここで，実関数wと複素関数w(z)の話をしていますが，関数の説明を軽くします。
　まず，実関数は，皆さんが普段から使っている？比例・反比例，１次関数や2次関数などのx，yで構成された関数です。
　次に，複素関数は，実関数と同様に普段から使っている？比例・反比例，１次関数や2次関数などのx，yで構成された関数の中に複素数z(=x+iy)が含まれた関数を指します。
　要するに複素数zを使っている関数か，否かの違いだけなのです。

　この一見すると，全く問題なさそうな実関数から複素関数への変換なのですが，大変な問題を抱えております。何が問題かというと，扱っている「2次元平面が違う」からなのです。
　実関数wのグラフは，x, yの変数を使った2次元グラフがかければよいので，xとyの情報さえあればグラフがかけます。
　しかし，複素関数w(z)のグラフは，複素数zを使った実部xと虚部 yの変数を使った2次元グラフをかくことになります。さらに2次元流れの速度成分u，vが必要になり，結局4つの情報が必要になるのです！
　図２に複素関数の曲線のイメージをそれぞれ示します。

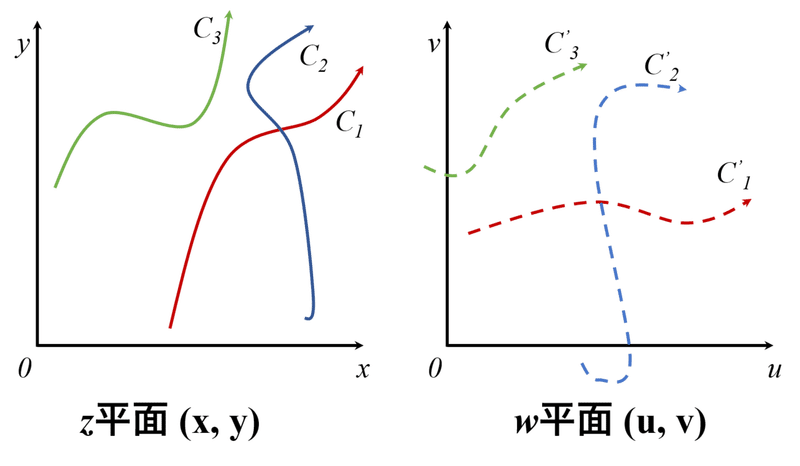
図２　複素関数の曲線

　あくまでもイメージですが，実関数から複素関数の4つの変数x, y, u, vが必要十分条件で結び付けられるのかが不明なのです。だからこそ，実関数と複素関数の「必要十分条件」が大事なのです。もし，実関数と複素関数の「必要十分条件」が成立するのであれば，式（１）のように表せます。

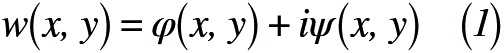
それでは，まず実関数と複素関数の「十分条件」を証明しましょう。

（２）実関数と複素関数の十分条件

　では，実関数と複素関数の十分条件を証明する準備を整えましょう。実関数wが複素関数w(z)となると仮定するため，次の例題を考えます。

【例題１】w(z)=z^2+z　（z=x+iy）
では，これを普通に解いてみましょう。式（２）に式変形の様子を示します。

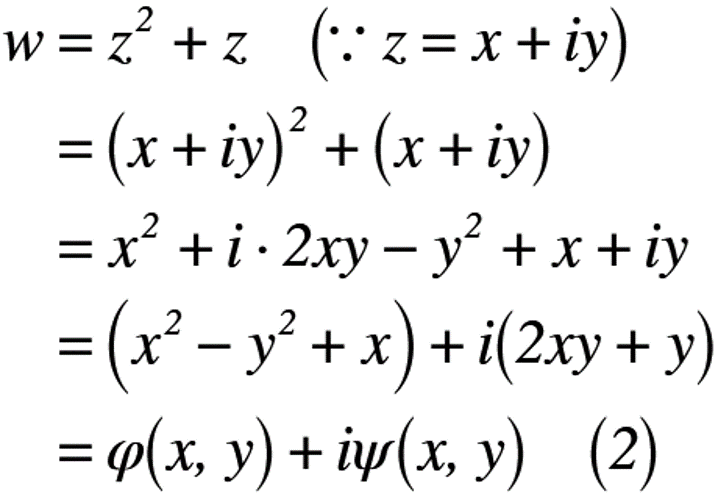
　まあ，何てことない普通の式変形でした。では，上式で出てきたφ，ψが同様に書くことができれば何も問題はないのですが，式（２）には「反例」が存在します（かなり大問題！）。
　そこで，限りなく同じではあるのですが，次の例題を考えましょう。

【例題２】w(z)=z_1^2+z_2　（z_1=x+iy，z_2=x）
では，これも普通に解いてみましょう。式（３）に式変形の様子を示します。

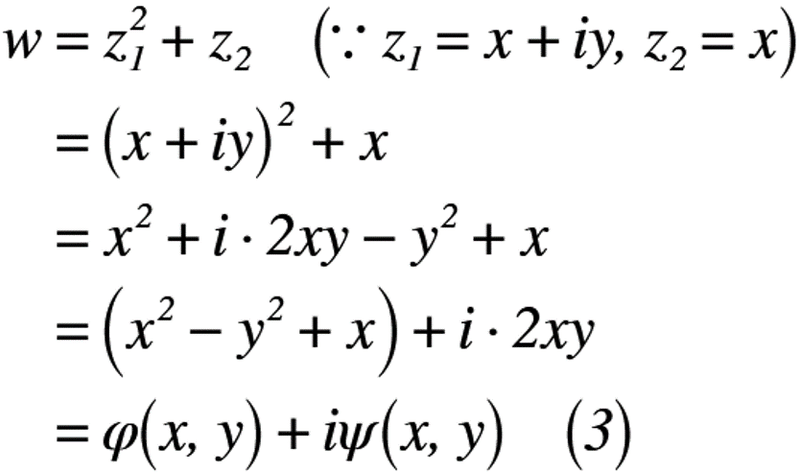
　このように式（２）と式（３）は，φ，ψが同様の式となっていないことが分かります。
　よって，残念なことに実関数と複素関数の十分条件は「偽」となる，すなわち十分条件とはならないのです。（まあ偽にはなっても，十分条件が成立するのですが，それは改めて説明する必要があるので，それはまたあとで…）

（３）実関数と複素関数の必要条件

　では，実関数と複素関数の必要条件を証明する準備を整えましょう。複素関数w(z)が実関数wとなるためには，複素関数が「正則（せいそく）である」こと，「連続である」ことが証明できれば，積分して原始関数に戻すことができます。
　要するに，微分可能な関数であることが分かればよく，さらに微分可能（＝正則）のときには必ず「コーシー・リーマンの微分方程式」が成立しているので，それを求められればよいのです。
　早速，複素関数w(z)をx, yについて合成関数の微分をすると，式（４）のように表せます。

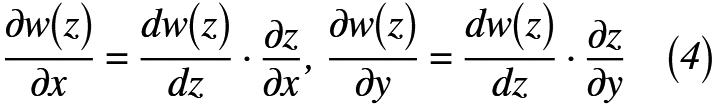
　また，複素数z(=x+iy)をx, yについて微分すると，式（５）のように表せます。

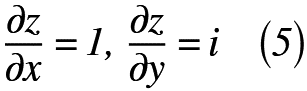
　ここで，式（５）を式（４）へ代入すると，式（６）のように表せます。

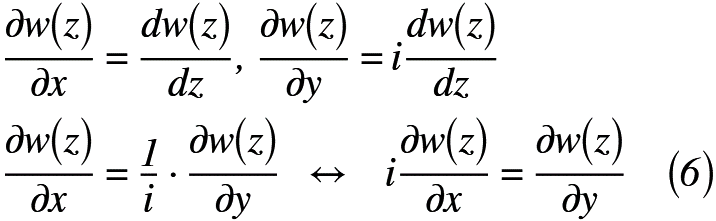
　では，複素数z(=x+iy)をx, yについてそれぞれ微分すると，式（7）のように表せます。

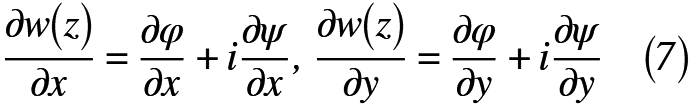
　式（６）を式（７）へ代入すると，式（８）のように表せます。

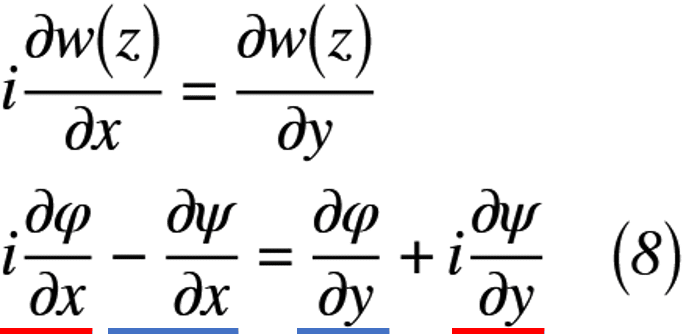
　式（８）の下線部をそれぞれまとめると，式（９）のように表せます。

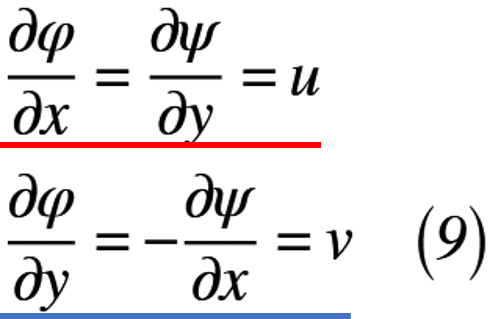
　この式（９）はまさに，あのコーシー・リーマンの微分方程式なのです！よって，実関数と複素関数の必要条件が成立することが分かりました。

（４）十分条件の偽を何とかするには…

　前項で示した通り，十分条件は不成立なのに対して，必要条件は成立することが分かりました。でも，十分条件が不成立なのは，反例が出てきたことよるものです。その反例をもう一度確認して頂ければわかる通り，複素数z(=x+iy)のうち，虚部yが零になることで成立しないのです（もし，複素数z(=x+iy)の実部xが零になったとしても，結果は同じです。）。
　そこで，この十分条件の反例については，なぜそのなったのかを説明ができれば十分条件を成立に持っていけます（何とも強引ではありますが，式の形が違う理由の説明ができることも大事ですからね…）。

　まず，複素数z(=x+iy)の全微分を考えると，式（１０）のように表せます。

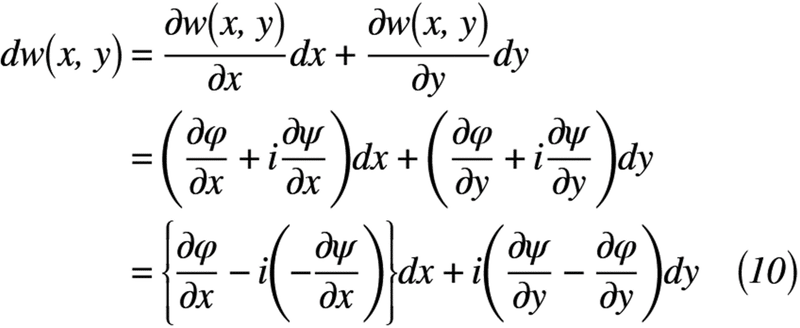
　何とも式（１０）は，よくわからない式変形をしているように見えますが，少し脱線します。でも，大事なことなので触れない訳にはいかないので，このような形をしています。
　式（９）を式（１０）へ代入すると，複素数zの全微分は式（１１）のように表せます。

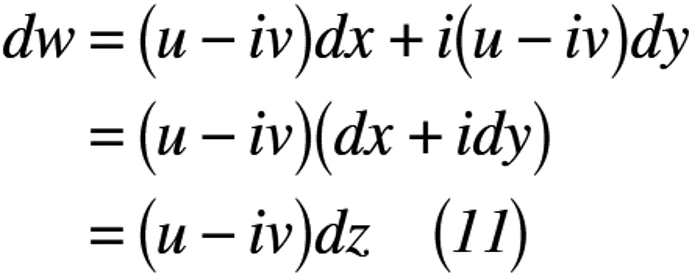
　ここで，wをzについて微分した式（１１）に登場するu+ivが複素速度，u-ivが共役複素速度といいます（複素関数のなかで出てくる共役関係を使った名称です。）。少し話が逸れましたが，前回の記事「複素ポテンシャル」でも取り扱いましたが，実はここで登場していることが分かりました。

　では，十分条件の偽を解決する続きをやっていきます。ここで，複素数z(=x+iy)をx, y, zについてそれぞれ微分すると，式（１２）のように表せます。

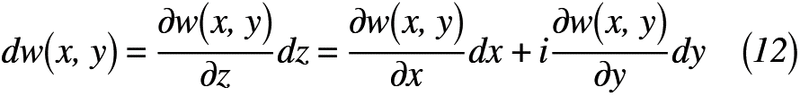
　ここで，複素数z=x+iyをx=z-iyへ変換し，式（１０）へ代入すると，式（１３）のように表せます。

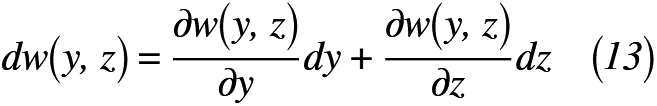
　得られた式（１３）から式（１０）を引くと，式（１４）のように表せます。

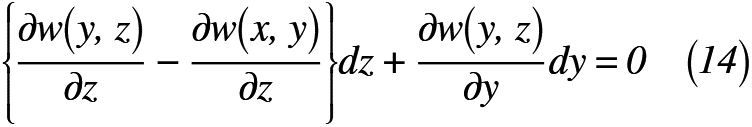
　先ほど，複素数z=x+iyをx=z-iyへ変換しましたが，このときの微分を合成関数の微分形式でかくと，式（１５）のように表せます。

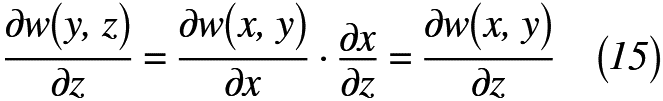
　よって，式（１５）を式（１４）に代入すると，式（１６）のように表せます。

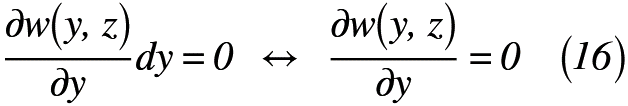
　式（１６）により，微分したら零になることから積分した複素数の値は，一定値または零であることが分かります。つまり，yに値が含まれない状態となります。すなわち，複素関数w(x, y)に複素数x=z-iyを代入すると，yが消去された状態のwがzのみの関数となります。
　したがって，反例も特別なパターンとして処理できるので，実関数と複素関数の十分条件は成立することが分かりました。

（５）まとめ

　今回の記事のまとめを以下に示します。
（１）実関数と複素関数の「必要十分条件」が成立するので，2次元流れを複素ポテンシャルとして表現できる。

　以上です。最後まで閲覧頂きありがとうございました。