皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第２６回目は，第２５回目で予告した通り，「鏡像のグラフ」について紹介していきます。

（１）鏡像の概要

　 では，「鏡像」について，再度復習します。鏡像の定義は，「複数（2つ以上）のわき出し，あるいは吸込みがお互いに向かい合う位置に影響を及ぼし合う状態が，あたかも鏡に映し出されている様子に類似していること」でした。つまり，数学的にはx軸，y軸もしくはその両軸に対称なグラフが描けることを意味しています。
　今回は，「2つのわき出し」が存在する場合を想定したうえで図１－１のような概略図を書いてみます。そして，今回のグラフ描画に必要な知識として「双曲線」を取り上げています。知らない方やもう一度確認したい方は以下の記事を参考にしてみて下さい。

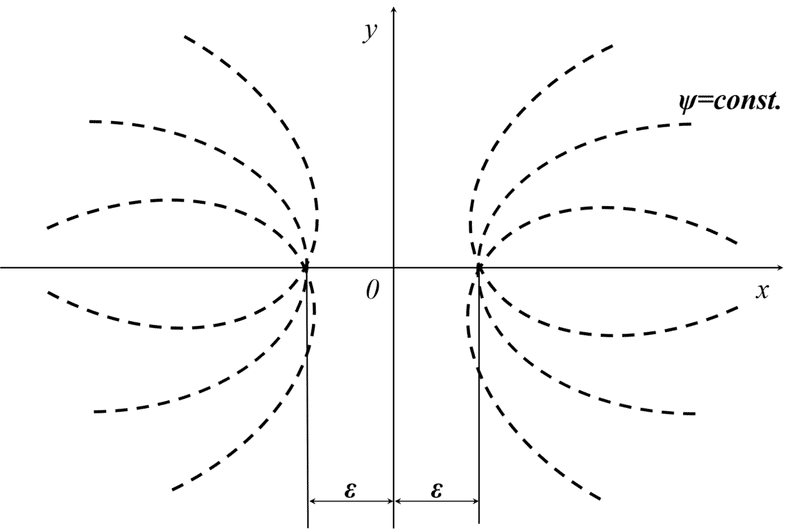
図１－１　鏡像の概略図（２つのわき出しの場合）

（２）鏡像のグラフ

（２―１）流線の式

　それでは，鏡像のグラフ描くために必要な式を確認していきましょう。まずは，2つのわき出しの鏡像を考えるときの複素関数は，式（１）のように表せます。

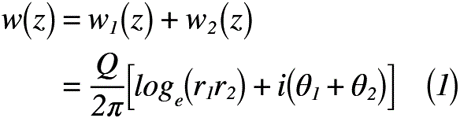
　ここで，式（１）を用いて，速度ポテンシャルφと流れ関数ψをそれぞれ導出することが出来ます。その結果，式（２）のように表せます。

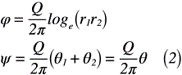
　今回のグラフ描画には，流れ関数のみを利用します。そのため，x軸とのなす角θを求めると，式（３）のように表せます。

　この式を使って，双曲線の一般式に必要な値を補っていくので，式（３）は非常に重要な役割を担います。また，今回の仮定としてψ=－0.9～0.9（0.1刻み）でθを算出します。
　次項では，双曲線の一般式と各値の関係を見ていきます。

（２－２）双曲線の一般式と各値の関係

　今回のグラフ描画には，双曲線の一般式を用います。そこで出てくるのは，a，b，x，yの4つの変数です。但し，xとyについては任意の値を設定できるため，後回しです。そのため，優先的に考える変数は，aとbの2つということになります。

　まずは，aを考えてみましょう。これは至って簡単です。双曲線におけるaは，双曲線の頂点の座標に該当するので，鏡像で使用する「x軸上の座標の一定値εと同様である」と考えることが出来ます。よって，式（４）のように表せます。

　式（４）にもある通り，x軸上の座標の一定値εは，任意の値を設定可能です。今回の仮定では，ε=±5とします。

　次に，bについて考えてみましょう。双曲線におけるｂは，漸近線が分かると答えに近づきます。双曲線における漸近線はy=(b/a)xとなります。そして，直線の傾きに該当するのは，(b/a)であり，三角関数ではtanθに該当します。つまり，漸近線の傾きはtanθとなるので，式（５）のように表せます。

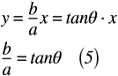
　なお，式（５）のθは，式（３）で得られた結果を代入することで最終的な値を算出できます。
　最後に求められたa，bは，式（６）のように表せる双曲線の一般式に代入して計算を行います。

　次項では，式（３）～式（６）までの結果を使って，表計算を行ったグラフ描画をしていきます。

（２－３）鏡像のグラフ描画

早速，グラフ描画のために計算を行います。式（３）を使って計算を行いますが，今回必要な仮定を以下に示します。

【仮定】わき出しの強さQ=4.0[cm^2/s]，x軸上の座標の一定値ε=±5，流れ関数ψ=－0.9～0.9（0.1刻み），変数x=－20～－5および5～20（１刻み）

　この仮定を使って，式（３）の計算結果を表１に示します。

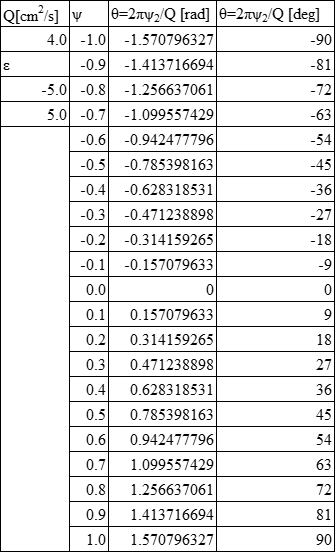
表１　式（３）の計算結果

　次に，式（５）を使った漸近線の計算結果を表２に示し，式（６）を使った双曲線の計算結果を表3にそれぞれ示します。

表２　漸近線の計算結果

表３　双曲線の計算結果

　ここで，鏡像の描画をいきなり示す前に，双曲線と漸近線の関係が成立しているかを確認してみましょう。図２－１にψ=－0.1のときの双曲線プロットと漸近線の関係，図２－２にψ=－0.9のときの双曲線プロットと漸近線の関係をそれぞれ示します。

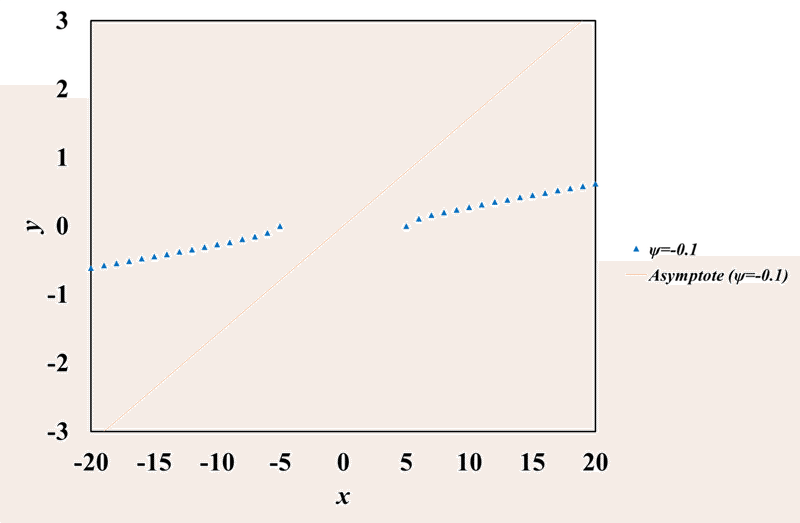
図２－１　双曲線プロットと漸近線の関係（ψ=－0.1の場合）

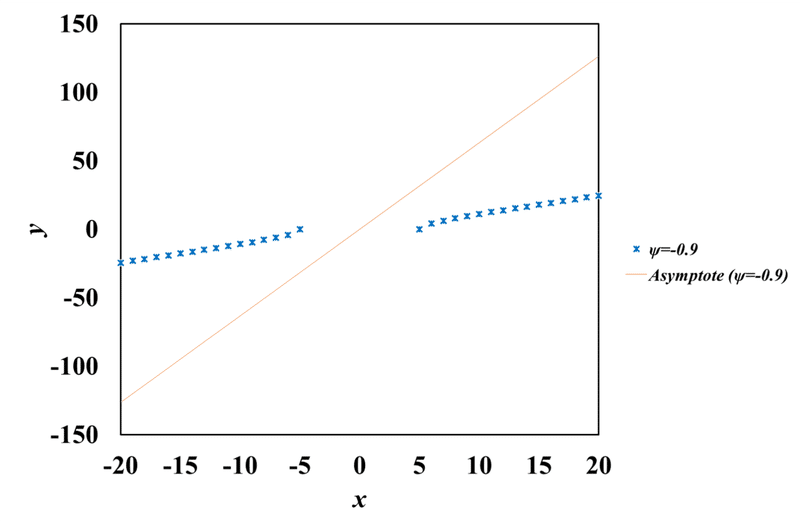
図２－２　双曲線プロットと漸近線の関係（ψ=－0.9の場合）

　図を見ると，いずれのグラフも双曲線プロットが漸近線を下回っていることが分かります。つまり，今回の双曲線グラフの描画は誤ったものではないことが確認できました。
　それでは，最終的に得られる鏡像のグラフを図２－３に示します。

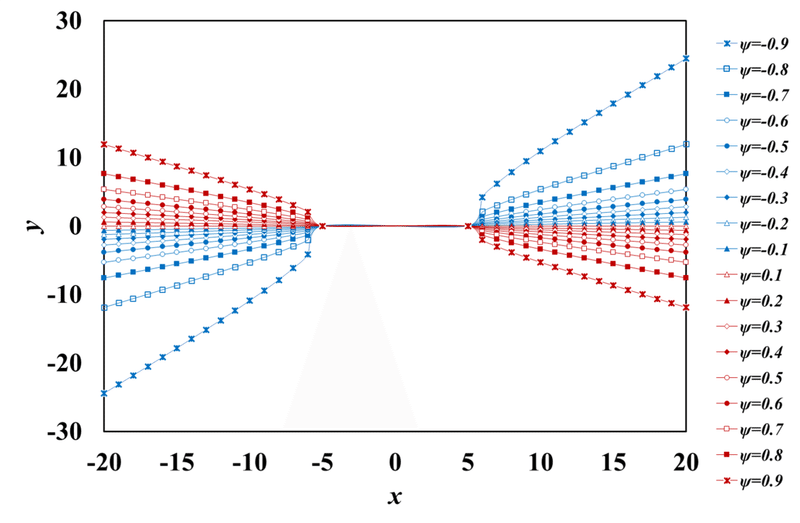
図２－３　鏡像のグラフ（２つのわき出しの場合）

　図を見ると，x軸上の座標の一定値εを起点にわき出しのグラフが双曲線で描けています。そして，グラフがx軸，y軸について対称なグラフであることから鏡像の定義が成立していることも分かります。
　今回は，2つのわき出しの場合を想定していましたが，例えば，1つのわき出しがy軸上にあって，かつy軸に対称な流れが描ける場合でも，鏡像の定義が成立するので「鏡像」となります。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）鏡像の定義は，「わき出し，あるいは吸込みがお互いに向かい合う位置にあたかも鏡に映し出されている様子のこと」を示す。
（２）わき出しが双曲線に従う場合，流れ関数を使うことで双曲線にある必要な変数を補いながら計算可能となる。
（３）2つのわき出しが鏡像となる場合は，x軸，y軸について対称なグラフとなり，双曲線と漸近線の関係を維持する。

　以上です。最後まで閲覧頂きありがとうございました。

　※次回は，任意の角度を回る流れについて扱う予定です。