皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　今回は，第２５回目に予定している「鏡像」で使用する予定の「双曲線」について紹介していきます。

（１）双曲線の一般形

　さて，今回の記事で取り上げる予定である「双曲線」についてですが，実は，現在の教育課程では最初に「2次関数」として中学3年で取り上げ，高校1年の数学Ⅰに再び「2次関数の一般形」をやった後に，高校3年の数学Ⅲで「双曲線」として取り上げられます。大学数学では，オイラーの公式を使うことで双曲線を表現できることも学びます（専門用語でカテナリーという名称で使われます）。今回は，高校3年で扱うものをメインに説明していきます。
　図１に今回取り上げる「左右対称な双曲線」の概略を示します（他には，上下対称もあります）。また，図１に左右対称な双曲線の一般式などもあわせて示します。

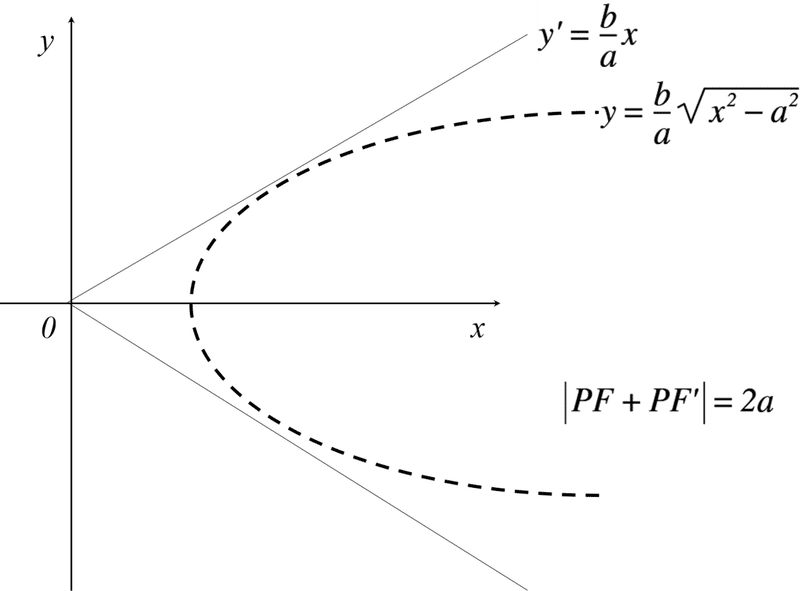
図1　左右対称な双曲線の概略

　この式を学ぶときは，問題を解けることに主眼を置かれるため，上式の証明は意外とやってもスルーされるのではないでしょうか（筆者本人の高専2年以来でした）。では，次項で式（１）の証明をしていきましょう。

（２）左右対称な双曲線の一般式の証明

　では，式（１）を証明する前に図１をもう一度確認しましょう。放物線・楕円・双曲線（2次曲線）で必ず出る焦点F（±c, 0）があります。幾何学で使われる「焦点」は，「２つの焦点からの距離の和が一定となるような点の軌跡」として定義することができます。そのため，曲線上の点Pと置くと，式（１）のように表せます。

　ここで，絶対値で表される式（１）を展開すると，式（２）のように表せます。但し，PF=√[(x-c)^2+y^2]，PF’=√[(x+c)^2+y^2]とそれぞれ置きます。

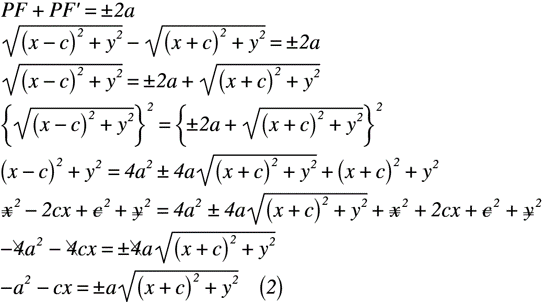
　この状態では不完全なので，両辺を2乗して展開すると，式（３）のように表せます。

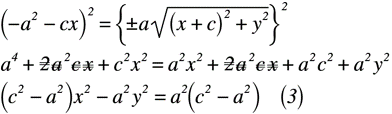
　ここで，三平方の定理（もしくは，ピタゴラスの定理）を思い出すと，c^2=a^2+b^2となります。但し，a：底辺，b：高さ，c：斜辺と置きます。式（３）に適用するために高さbを基準にすると，式（４）のように表せます。

　式（４）を式（３）へ代入すると，式（５）のように表せます。

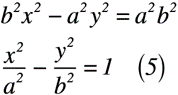
　式（５）が，（左右対称な）双曲線の一般式と呼ばれるものです。注意なのが，上式のような双曲線には必ず漸近線が存在します。次項では，双曲線の一般式と漸近線の関係を見ていきます。

（３）双曲線の一般式と漸近線の関係

　では，再び図１を確認していきましょう。双曲線の一般式は式（５）から分かりますが，漸近線はy’=(b/a)xとなります。この関係は，図1の第一象限（x，yともに正の値となる領域）でのみ適用できるものです。
　ここで，漸近線とは何か説明しましょう。漸近線の定義とは，「十分遠くで曲線との距離がゼロに限りなく近づき，曲線と接しない直線」のことを指します。つまり，ここで説明する「双曲線の一般式と漸近線の関係」は，「定義が本当に成立しているのか」を証明することになります。
　式（６）に，第１象限における双曲線の一般式と漸近線の差を示します。

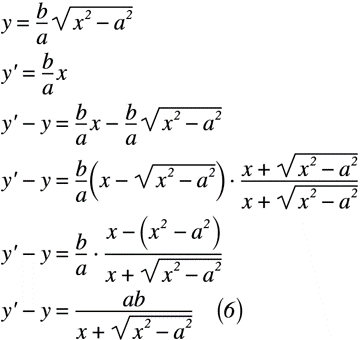
　ここで，式（６）のxについて極限を取ると，式（７）のように表せます。

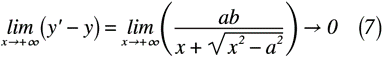
　式（７）はxの値を限りなく大きくした場合を想定しています。この場合，分母の値がかなり大きい値（無限なので，分かりやすく1億や1兆としても感覚的には問題ない）となります。それに対し，分子の値はせいぜい十・百の位の値です。
　つまり，分子の値は分母の値と比較して，圧倒的に小さいことが分かります（小数点第何位になるのかは想像つかないレベルです）。
　よって，あまりに小さい値となるので，「ゼロに収束する」と仮定するのです（通常の場合，小数点第４位の値であればゼロ近似が可能になります）。これが，「十分遠くで曲線との距離がゼロに限りなく近づく」の解答です。

　注意なのは，xを無限としていることです。言い換えると，「有限ではない」ということです。しかし，私たちが使う値の範囲は基本的に有限です。実際の条件では「無限」は仮定の考え方であり，実際には成立しないのです。
　よって，xの値を大きくすれば「ゼロ」には近づきますが，決して「ゼロにはならない」のです。これが，「曲線と接しない」の解答です。

　同様に，第4象限（xが正，yが負の領域）でも成立するかを証明します。式（８）に，第4象限における双曲線の一般式と漸近線の差を示します。

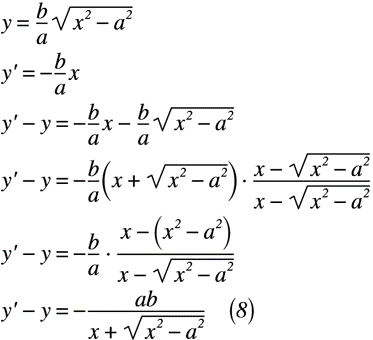
　ここで，式（８）のxについて極限を取ると，式（９）のように表せます。

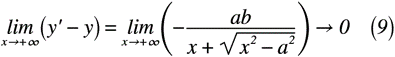
　このように，式（９）で得られる結果は，式（７）の結果と同様になります。今回は取り上げませんでしたが，第2象限（xが負，yが正の領域）は式（９）と同様の結果，第３象限（x, ｙがともに負の領域）は式（７）と同様の結果が得られます。
　これより，どの象限でも双曲線と漸近線は，「十分遠くで曲線との距離がゼロに限りなく近づき，曲線と接しない」ということが分かりました。

（４）まとめ

　今回の記事のまとめを以下に示します。
（１）双曲線は，左右対称と上下対称の2種類存在する。
（２）双曲線の一般式は，2つの焦点距離→三平方の定理で証明可能である。
（３）どの象限でも，双曲線と漸近線の関係は，「十分遠くで曲線との距離がゼロに限りなく近づき，曲線と接しない」ことが証明可能である。

　以上です。最後まで閲覧頂きありがとうございました。

※本記事は，「鏡像」にて使用する背景知識です。もしかしたら，その他にも使うかもしれませんが…。