皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第１７回目は，第１６回目で予告した通り，「一様流れとわき出しの合成」について紹介していきます。

（１）ポテンシャル流れの合成ができると？

　さて，今後の記事で取り上げる「一様流れとわき出しの合成」についてですが，基になる理論として「ポテンシャル流れの合成」があります。これについては，以前の記事で紹介していますので，知らない方は確認してみてください。

　では，「一様流れとわき出しの合成」を行いますが，いきなり言われても分からない方は，以前の記事を確認してみてください。
　但し，今回は分からなかったとしても問題はありません。なぜなら，結論が分かっているためです。皆様が流れの様子を見て，納得できるかはさておき，図１に一様流れとわき出しの合成の概略図を示します。ポテンシャル流れの合成ができると，今までの流れからは想像できない新たな流れ場を図示できるようになります。

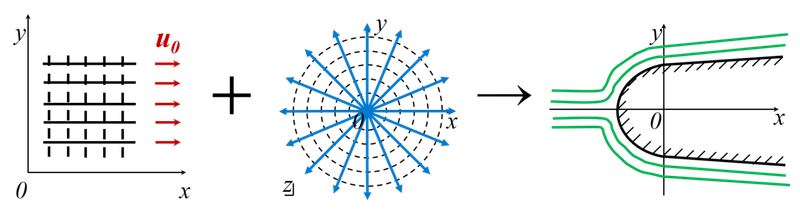
図１　一様流れとわき出しの合成の概略図

　図1の合成図を描くには，それに見合った数式が記述できることが必要です。次項で早速，ポテンシャル流れの合成を数式に使っていきましょう。

（２）一様流れとわき出し

（２－１）複素ポテンシャル

　早速，ポテンシャル流れに必須な「複素ポテンシャル」を求めていきます。以前の「ポテンシャル流れの合成」で取り扱ったように「重ね合わせ」ができることを解説しました。すなわち，全く関係のない関数を「足し合わせる」ことができます。よって，一様流れとわき出しの複素ポテンシャルは，以前の記事で解説しているものを使うと，式（１）のように表せます。

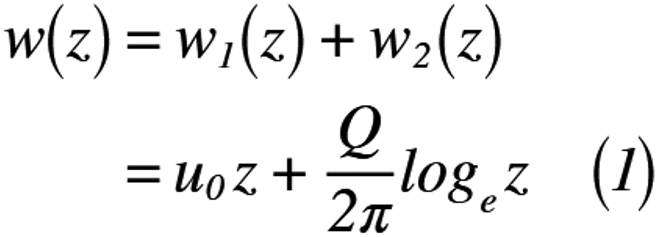
　但し，u0は速度，Qはわき出しの強さをそれぞれ示します。

（２－２）速度ポテンシャルと流れ関数

　式（１）で示した複素ポテンシャルから速度ポテンシャルφと流れ関数ψをそれぞれ考えます。式（２）に複素ポテンシャルの計算結果を，式（３）に式（２）の比較で確認できる速度ポテンシャルと流れ関数をそれぞれ示します。

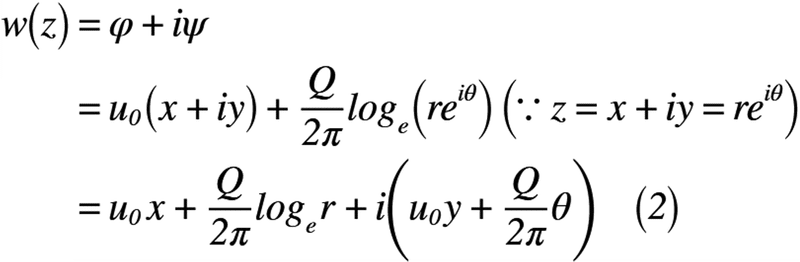
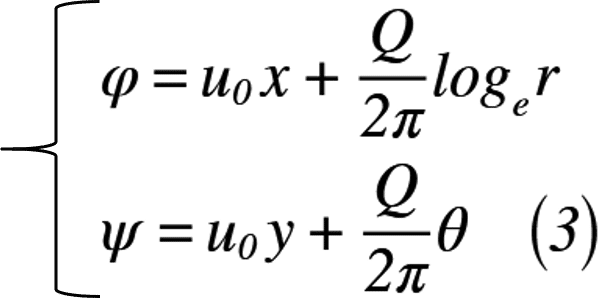
　ここで，極座標となっている「わき出し」の半径rとx軸とのなす角θについては，直交座標へ変換が必要になるので，変換した結果を式（４）のように表します。

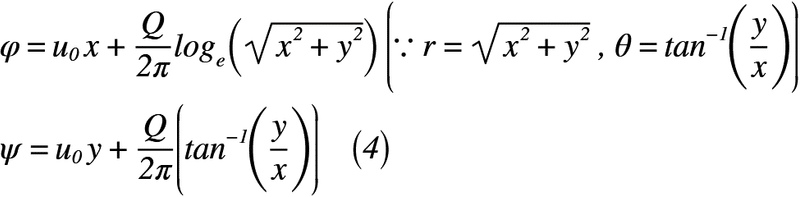
（２－３）よどみ点

　いきなり出てきました流体力学の専門用語です！
　結論から言うと，「よどみ点」とは，「流速が零になる点」のことを指します。

　もう少し，専門的に言うと，「流速が零になることでベルヌーイの定理が成立する場合，圧力が最大となる点」です。解説等はまだしていませんが，流体の測定機器として知られている「ピトー管」がこの理論を利用することで流速を求めています。ちなみに，豆知識をお話しすると，時速300kmにわずか数秒で到達するF1カー（フォーミュラーカー）のフロントウィング接合部付近には必ず「ピトー管」がついています（折り曲げたL字のストローのようなもの）。
　また，最近では，期間がかなり制約されている合同テストなどでは，サイドポンツーン（F1カーの運転席の左右部分）にピトー管の集合体である「エアロレイク」というものが付くこともあります。以下に参考URLを示します。

　さて，話が逸れてしまいましたので，この「よどみ点」を複素ポテンシャルへ適用しましょう。複素ポテンシャルを複素数zについて微分すると，複素速度が求まります。ここで，複素速度に対して，「よどみ点」の「流速が零」になる性質を用いることができます。この性質は，機械工学ではよく使います。微分積分の幾何学の世界では，微分して零になる場合に最大値，もしくは最小値が求められることが知られています。これが関数のいわゆる「極値」（関数の最大値・最小値の切り替わる値）になるため，定量的（数値を用いて議論すること）に評価するときには非常に有効なのです。
　この性質を使い，式（１）を複素数zについて微分すると，式（５）のように半径rとx軸とのなす角θが表せます。

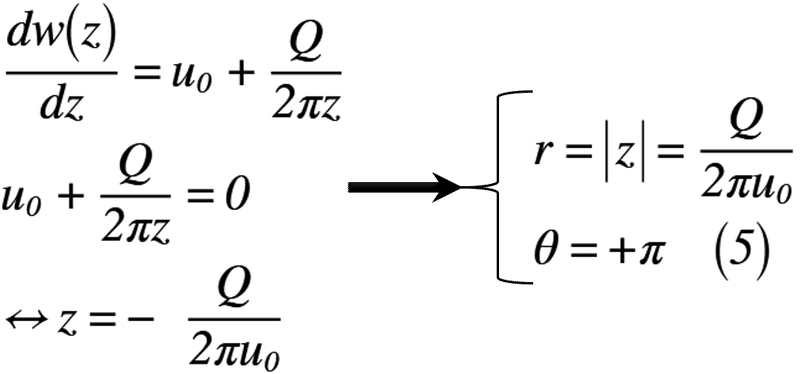
　これにより，よどみ点の座標は（－Q/2πu0, 0）となります。

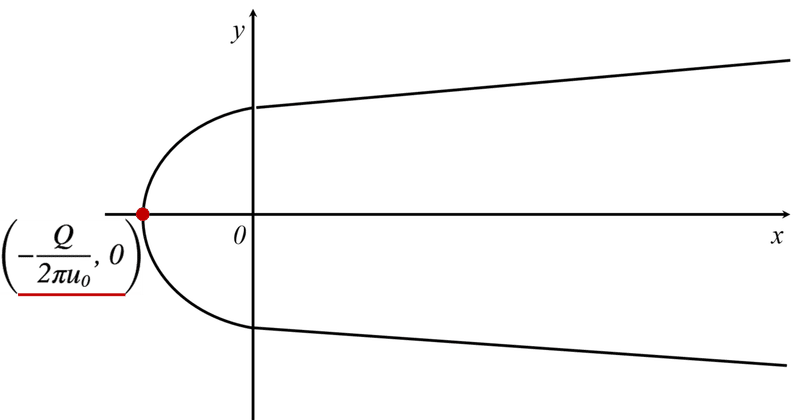
図２　よどみ点の座標

（２－４）よどみ点が通る流線とy軸との交点

　前項では，放物線のよどみ点の座標を算出しました。図１の概略図から分かるように，よどみ点を通る線は「放物線」となり，よどみ点の座標から放物線の「始点」が分かります。しかし，これだけでは，y軸のどこを通るかが不明なので，y軸との交点を算出することで放物線を１本に絞ることができます。

　そこで，よどみ点が通る流線とy軸との交点を算出するためには，「よどみ点」の情報と「流れ関数」の情報が必要となります。よどみ点のx軸とのなす角θを使って，流れ関数を記述すると，式（６）のように表せます。

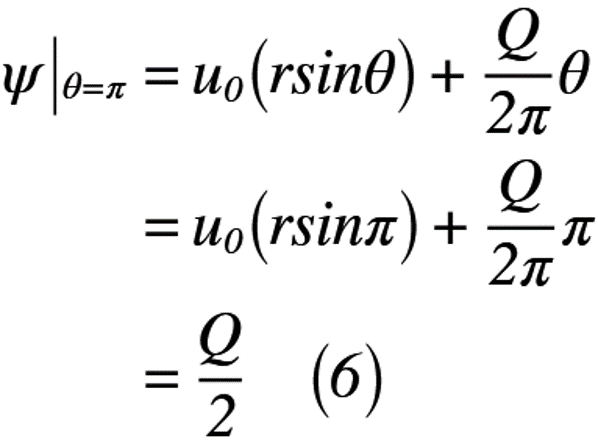
　式（６）を式（３）の流れ関数に代入すると，式（７）のように表せます。

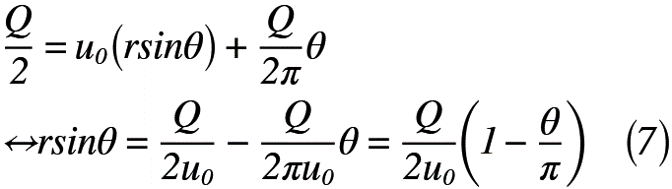
　では，図１の合成図および流線とy軸との交点を考えると，x軸とのなす角θは，π/2，3π/2の２つ考えられるので，式（７）に代入して考えると，式（８）のように表せます。

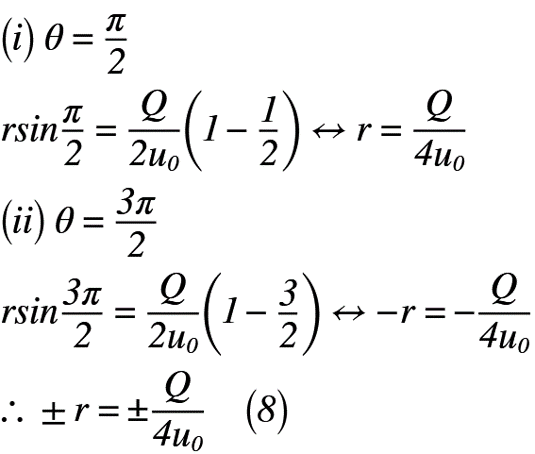
　よって，よどみ点が通る流線とy軸との交点は（0, ±Q/4u0）となります。

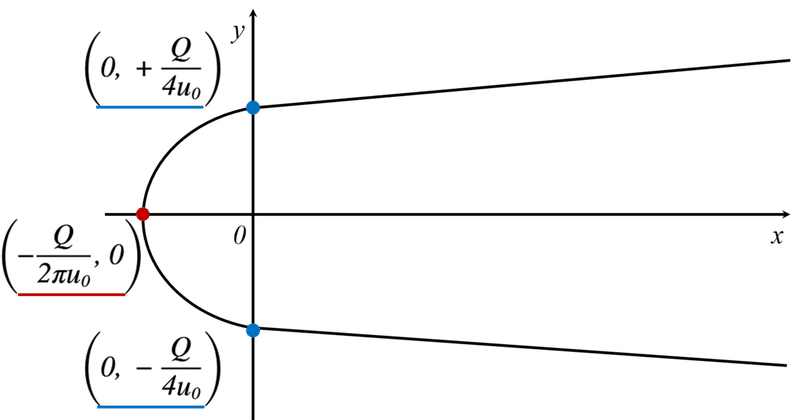
図３　よどみ点が通る流線とy軸との交点

（２－５）漸近線

　ここまでに，放物線のよどみ点及び流線とy軸との交点の座標を算出しました。放物線には，必ず「漸近線」があります。漸近線は「十分遠くで曲線との距離が零に近づき，かつ曲線が接しない直線」のことを指します。そのため，図1の合成図に示すような放物線にも「漸近線」が存在します。
　ここで，x軸の正方向を考えると，x軸とのなす角θは，0，2πの2つ考えられます。y座標は式（７）に代入すると，式（９）のように表せます。

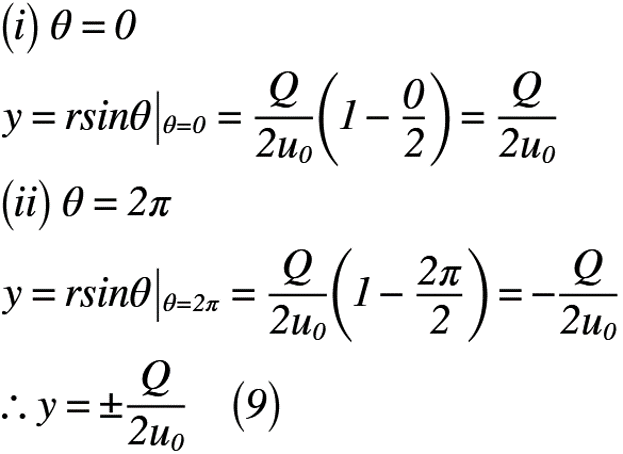
　よって，漸近線はy=±Q/2u0となります。

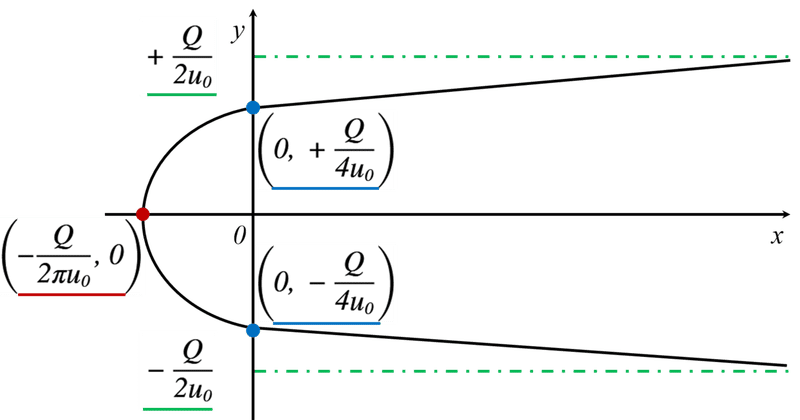
図４　漸近線

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）一様流れとわき出しの合成することで，放物線上に沿うような流れ場を再現できる。
（２）放物線には流速が零の点，いわゆる「よどみ点」が存在する。
（３）「放物線」を描くには，「流線とy軸との交点」と「漸近線」が必要となる。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，一様流れとわき出しの合成のグラフについて扱う予定です。