生物の「成長」は細胞数が増え、体が大きくなることだと考えられている。
しかし、受精卵の「卵割期」はそうではない。

＜卵割期＞
受精卵の初期の細胞分裂の様子は不思議である。受精卵の大きさは一定のまま、細胞の数が「２」、「４」、「８」と増加する。したがって、個々の細胞はどんどん小さくなる。それで、この時期の細胞分裂を「卵割」と呼ぶ。次図は４０時間経過したヒトの受精卵の様子を表しているという。

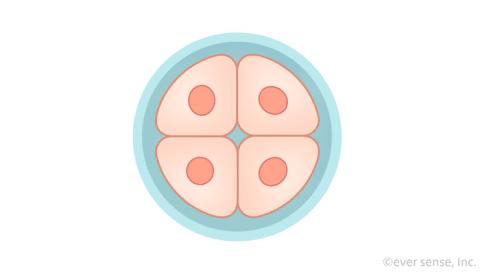
＜外部に自己相似な図形が・・・＞
生物を含めて、鉱物や結晶などあらゆる自然界の「成長」を探る数学上の
一つの視点に「自己相似性」がある。
 　　　　　
典型的な例は、一辺が「１」の正方形一個から始まり、それが二個になり、一辺の長さが「２」、「３」、「５」、「８」と大きくなる次図のような
正方形の連鎖である。

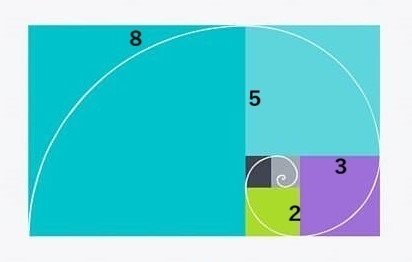
この連鎖から浮かび上がる螺旋形は「貝殻や台風等の成長」の様子を表す。
（外側の長方形は黄金比に近づく。）
相似な図形が増殖し、外形が大きくなる様子は一つの「成長」の典型である。
 
ちなみに、半導体の製造には、基盤の上に核となる結晶の原子の配列等を保ったまま結晶を「成長」させる「薄膜結晶生成技術」が必要だという。
 
＜内部に相似な図形が・・・＞
次に、受精卵のように、外形の大きさは一定で変わらず、その内部に相似な図形が個数を増すような「成長」のモデルを図示してみる。
ここで、外形の大小は「面積」を比較していることに留意したい。

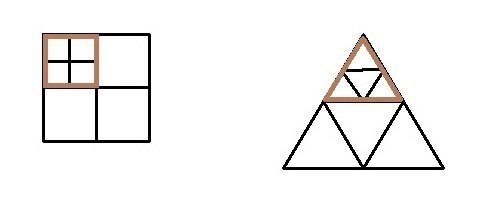
外形が一定で変わらないのは「面積が一定」であることである。しかし、内部はどんどん複雑に「成長」している。

＜二つの成長＞
つまり、自然界や人工的な結晶などの「成長」には、大別して外形が大きくなる「増殖成長」と、外形の変化はほとんど無く、内部が複雑になる「充実成長」の二種が存在することになる。そして、その二種の「成長」は互いに補い、あるいは交互に繰り返して目標となる姿にたどり着くのである。

ところが、細胞を増殖して外形を大きくする「増殖成長」には、癌細胞のように成長が暴走する場合がある。そして、目標とする姿とは異なる様相を呈することになる。

＜不思議な図形＞
同じように、内部が複雑になる「充実成長」においても困惑する場合がある。成長が限りなく続き、その結果として不思議な図形が表れることがある。次図はポーランドのシェルピンスキー（１８８２～１９６９）の「正三角形」である。

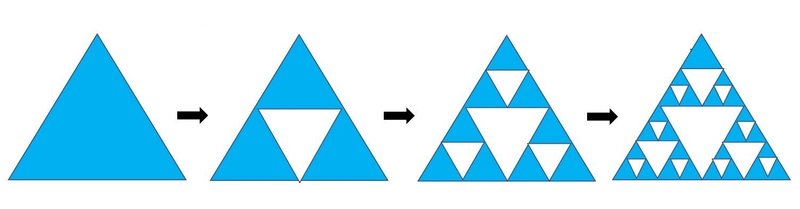
 正三角形の内部に「１／２」の正三角形を四個増やし、中央の一個を消去する。残りは「３／４」である。
これを限りなく続けた最終の姿は想像できるだろうか。
「面積はゼロ」になり、輪郭線はステップごとに「３／２」ずつ増加して無限大になってしまう。まるで、穴だらけのフィルターのようである。
（最終的には面積が無く、触れることもできない不思議な図形になる。）

正方形においても同様な図形が出現する。
次図のように、正方形を９等分して中央の正方形を消去する。すると、面積が「８／９」に減少し、境界線は「４／３」に増加する。

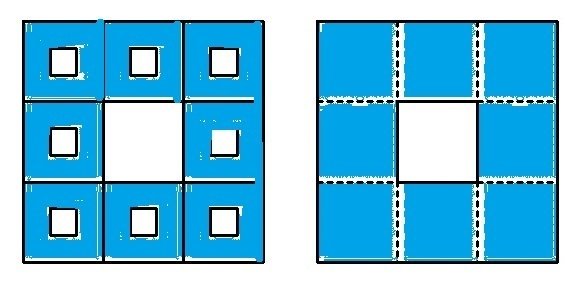
この操作を限りなく続けると「面積ゼロ」で「境界線が無限大」の図形にたどり着く。
 
なお、「正方形」を「立方体」に変えて、六面すべてにおいて上図になるように小さい立方体を「７個取り除く」操作を限りなく続けることにする。
すると、次図のような穴だらけの立方体図形（メンガーのスポンジ）になる。

この操作は１ステップ進めるごとに、体積は「7 / 27」ずつ減少するので最終的な図形の「体積はゼロ」になる。
 
＜充実成長の意味＞
さて、「充実成長」の例として示した正三角形や正方形の場合について整理しておく。
（１）中央部分の小さい正三角形や小さい正方形を「取り除く」場合と「取り除かない」場合
（２）「充実成長」のステップを有限に留めるか無限に続けるか。
 
（１）については、受精細胞の「卵割」と、水分や養分を運ぶ「血管」や「導管」の生成を連想するモデルになっている。
 
（２）については、有限な「充実成長」こそ生物にとって有益であり、無限に続く「充実成長」は「暴走」に近いことを示すモデルになっている。
 
＜相似次元の定義＞
中央部分を取り除く操作を限りなく続けてたどり着く不思議な図形について、数学は次のような「相似次元」を定義している。
正三角形も正方形も最終的な図形は「面積ゼロ」なので「次元２」は該当しない。もちろん「次元１」でもない。
 
それで、「１／２」の正三角形を基にすると、元の正三角形は「４個分」であるから「相似次数」を「log4 / log2＝2」と定めることにする。

もう少し詳しく述べると、「１／２」の正三角形を基にすると元の正三角形の一辺の長さは「２個分」である。そして、元の正三角形の面積は「４個分」で「２の２乗」である。
そこから、べき乗の「２」を「次数」と定義している。

すると、中央の小さい正三角形を一個取り除く操作を限りなく続けてたどり着く不思議な図形の次数は、一つのステップにおいて、面積は「３個分」になるので「2＾x＝3」となる。
このことから、次数ｘは「log3 / log2≒1.58」となる。
 
同様に、体積がゼロになる「メンガーのスポンジ」の次数は「３」ではありえない。
小さい「１／３」の立方体二十七個（＝３の３乗）で元の立方体になるので、元の立方体の次数は「３」である。
ところが「七個の小さい立方体を取り除く」ので、残りは二十個であるから「3＾x＝20」となり、メンガーのスポンジの次数は「log20 / log3≒2.73」となる。

＜コッホ曲線の次数＞ 
ところで、「コッホ雪片」は「２次元」図形の正三角形が基になっているように見えるが、実は「１次元」の折れ線を三本あわせたものが基になっている。
 
長さ「１」の線分を「１／３」にした短い線分を基にすると元の線分は「３個分（＝3＾1＝3）」である。それで、元の線分は「１次元」の図形であることが分かる。
そこから、コッホは変形操作を始める。一つのステップで短い線分を「４個分」の「曲線」にするのである。

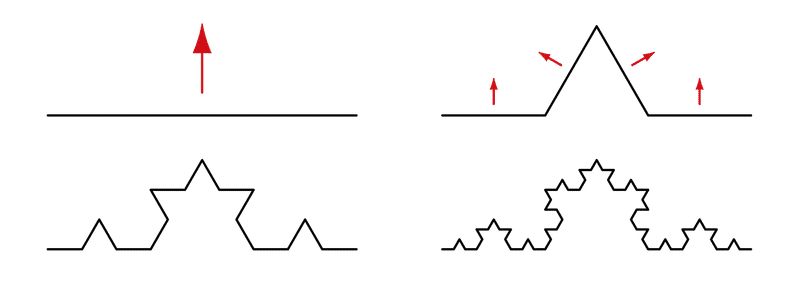
このステップを限りなく続けてたどり着いたのが「コッホ曲線」であり、「コッホ雪片」である。
　したがって、コッホ曲線の次数は「3＾x＝4」であるから次のようになる。　→　 log4 / log3 ≒ 1.26
 
＜自然の中の自己相似性＞
最後に、自己相似図形を中心としたフラクタル理論は自然界の姿の解析に活用されている。台風の形や進路の予想は身近な例である。
なにより、一枚の葉の形と大樹の形が似ていることに驚くことがある。
次の写真はシダの実物ではなく、フラクタル理論を用いて描いた人口のシダの葉である。