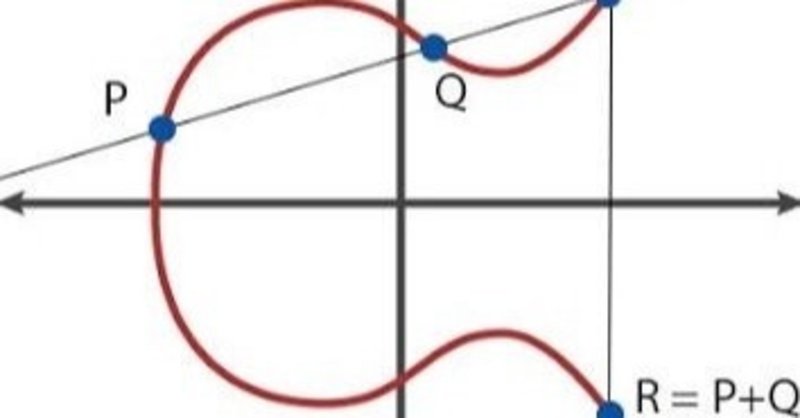
Diffie-Hellmanと楕円曲線
前回、軽く対称鍵暗号について話した。しかし、鋭い読者は既にお気づきだろうが対称暗号には問題がある。それは、鍵の受け渡しである。例えば、暗号化された通信を復号化するために、通信相手に暗号鍵を送る必要がある。しかしここで第三者が通信を傍受しており、それにより鍵が盗まれたしまった場合、暗号化された通信を全て復号化されてしまう。
そこで今回はDeffie-Hellmanという暗号鍵を暗号化するための手法と楕円曲線を使ったシステム(合わせてECDH: Elliptic Curve Deffie-Hellmanと呼ばれる)を見ていこう。少々難易度が高い内容だが、諦めずに最後まで読んでいただければ通信だけではなく、暗号通貨でも使われてる知識が身につくだろう。
まずはじめにざっくりと大まかな流れを見ていくためにAliceとBobに登場していただこう。
AliceとBobはそれぞれ秘密鍵, aとbを持っており、とあるオペレーションGをAliceはaの回数だけ行い公開鍵A=aG, BobはB=bGを作る。
ここで重要なのは、このオペレーションで得たaGとbGは非可逆で、例えAとGが分かったところでA/G=aの様にaを計算できない。AとBをそれぞれ計算できたら、AliceはBobにAを送り、Bを受け取る。Aliceは受け取ったBからaBを計算し、BobはbAを計算する。
この時、交換法則は成り立つのでaB = abG = baG = bAになり、お互いこの値を使って対称鍵を交換する。ちなみに、この値をそのまま使わない理由としては、対称鍵の方がセキュリティレベルが高いのと、速度の問題からである。 楕円曲線を使った暗号は256ビットの鍵の長さでAESの128ビットのセキュリティレベルがあるのに対し、一般的に使われている対称暗号は256ビットのセキュリティレベルがある。(ついでに、もう一つよく使われているRSAという非対称鍵暗号で128ビットのセキュリティレベルのために必要な鍵の長さは3072ビットである。)
では、この楕円曲線を使った暗号の仕組みをCurve25519を例に見ていこう。
Curve25519とは楕円曲線の一種のMontgomery Curveで以下の様に定義されている。
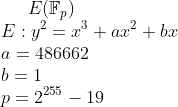
これは、この曲線が2^255-19(これがCurve25519の名前の由来)の素数の有限体の上で定義されていることを意味する。といっても、数論に詳しくない人は何を言っているのかさっぱりだと思うのでコードや実例を挙げる。
まず、x=9の時、右辺の値は39420360となる。「2^255-19の有限体の上で定義されている」とはy^2を2^255-19で割った時の余りが39420360となる様な整数yのことである。
これはTonelli-Shanks Algorithmを使って求められる。(下記はPythonのコード)
https://en.wikipedia.org/wiki/Tonelli%E2%80%93Shanks_algorithm
def legendre(a, p):
return pow(a, (p - 1) // 2, p)
def tonelli(n, p):
assert legendre(n, p) == 1, "not a square (mod p)"
q = p - 1
s = 0
while q % 2 == 0:
q //= 2
s += 1
if s == 1:
return pow(n, (p + 1) // 4, p)
for z in range(2, p):
if p - 1 == legendre(z, p):
break
c = pow(z, q, p)
r = pow(n, (q + 1) // 2, p)
t = pow(n, q, p)
m = s
t2 = 0
while (t - 1) % p != 0:
t2 = (t * t) % p
for i in range(1, m):
if (t2 - 1) % p == 0:
break
t2 = (t2 * t2) % p
b = pow(c, 1 << (m - i - 1), p)
r = (r * b) % p
c = (b * b) % p
t = (t * c) % p
m = i
return r
上の関数に
tonelli(39420360, 2**255-19)を代入すると
y = 14781619447589544791020593568409986887264606134616475288964881837755586237401
が求められる。一応チェックのために
pow(y, 2, 2**255-19)と入れると39420360が得られるのが確認できるだろう。ちなみにx=9はCurve25519の開始点として使われ、
G = (9, 14781619447589544791020593568409986887264606134616475288964881837755586237401)と定義する事にする。これを一般化して楕円曲線上のとある点、Pへの演算、自身を2倍にすると点Qを足す、を見ていく事にする。
Point Doubling
まず、楕円曲線上の点Pから2Pの座標を求める。
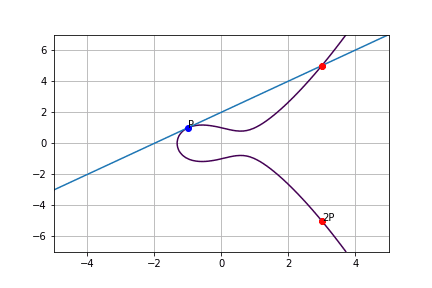
イメージとしては点Pに対して接線を引く。その接線と楕円曲線の交点(x, y)をx軸に対して反転させた座標(x, -y)が2Pである。これを繰り返す事で4P, 8P, 16P・・・と求めていくことができる。式にすると、
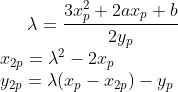
の様に、まず接線の傾きを楕円曲線を微分して求め、あとは元の式に代入するだけである。Gを例にとると、2Gの座標は
2G=(14847277145635483483963372537557091634710985132825781088887140890597596352251, 48981431527428949880507557032295310859754924433568441600873610210018059225738)となる。
Point Addition
R=P+Qを求める時、基本的に上と同じで、微分を計算する代わりに普通に傾きを計算すればいい。
つまり
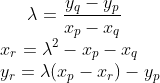
となる。
これにより、例えnが大きな数字だとしても、nを二進法に変換してそれぞれの桁に対応する2の乗数のGを足し合わせることでnGが簡単に計算できる。
例えばn=1337の場合、2進法で10100111001なので1337G = G+8G+16G+32G+256G+1024Gで計算することが可能である。
では、実際にコードを書いてみると下の様になる。
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
class Elliptic_Curve():
def __init__(self, a, b, p, x):
self.a = a
self.b = b
self.p = p
self.x = x
self.n = x**3+a*x**2+b*x
self.G = (x, tonelli(self.n, self.p))
def reset_G(self, x):
self.G = (x, tonelli(self.n, self.p))
def double(self, point):
s = (3*point[0]**2+self.a*2*point[0]+self.b)*modinv(2*point[1], self.p)
x = (s**2-self.a-2*point[0])%self.p
y = s*(point[0]-x)-point[1]
z = -y%self.p
return (x, y, z)
def add(self, point_0, point_1):
if point_0 == 0:
return point_1
else:
s = (point_1[1]-point_0[1])*modinv((point_1[0]-point_0[0])%self.p, self.p)
x = (pow(s, 2, self.p)-point_0[0]-point_1[0]-self.a)%self.p
y = (s*(point_0[0]-x)-point_0[1])
z = -y%self.p
#t = tonelli(x**3+self.a*x**2+self.b*x, self.p)
return (x, y, z)
def get_pubkey(self, privkey):
#self.set_privkey(privkey)
b = bin(privkey)[2:]
total = 0
pt = self.G
for i in b[::-1]:
if i == '1':
total = self.add(total, pt)
#total += pt[0]
pt = self.double(pt)
return total[0]
def get_shared_key(self, pubkey_other, privkey):
x = pubkey_other
n = x**3+self.a*x**2+self.b*x
self.G = (x, tonelli(n, self.p))
shared_key = self.get_pubkey(privkey)
self.reset_G(self.x)
return shared_keyここで、上のコードを使い、Alice, Bobに再度登場してもらい、通信を傍受しているEveにバレない様に共通鍵を実際作ってみる。
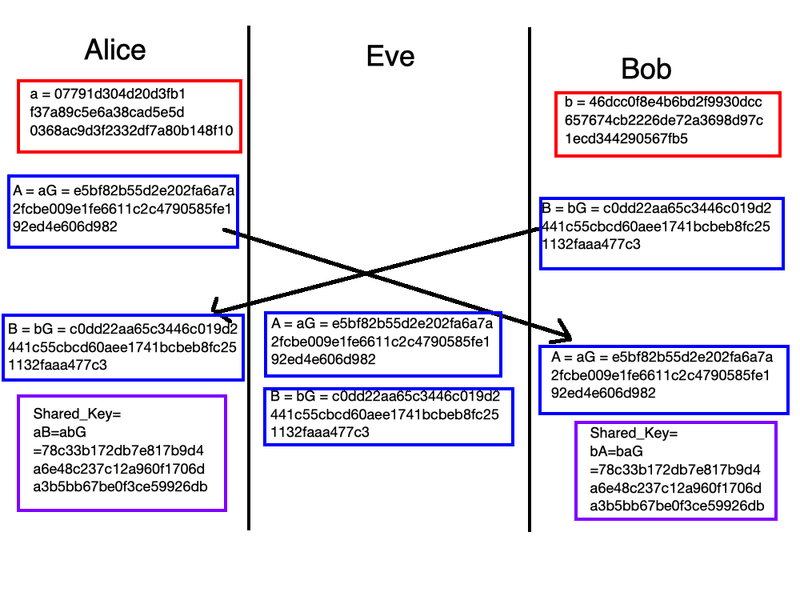
まず、Curve25519のパラメーターに基づいて楕円曲線を下の様に定義する。
ec = Elliptic_Curve(a = 486662, b = 1, p = 2**255-19, x = 9)まず最初に、Alice, Bobはそれぞれ秘密鍵
a = 07791d304d20d3fb1f37a89c5e6a38cad5e5d0368ac9d3f2332df7a80b148f10
b = 46dcc0f8e4b6bd2f9930dcc657674cb2226de72a3698d97c1ecd344290567fb5を持っている。そして、それを元に公開鍵
A = aG = e5bf82b55d2e202fa6a7a2fcbe009e1fe6611c2c4790585fe192ed4e606d982
B = bG = c0dd22aa65c3446c019d2441c55cbcd60aee1741bcbeb8fc251132faaa477c3が作られ(ちなみに一般的に鍵はx座標の値のみ使われる)、AliceにBが、そしてBobにAが送られる。ここで初めて、通信を傍受していたEveにAとBを手にする。
そして、無事にBobの公開鍵Bを手に入れたAliceは自分の秘密鍵aとBobの公開鍵Bを使って
aB = 78c33b172db7e817b9d4a6e48c237c12a960f1706da3b5bb67be0f3ce59926dbを計算し、同じ様にBobも
Ba = 78c33b172db7e817b9d4a6e48c237c12a960f1706da3b5bb67be0f3ce59926dbが得られる。この二つの値が同じであるため、AliceとBobはこの値で対称鍵を暗号化し、交換することで暗号化された通信を行うことができる。
しかし、EveはAとBを持っているものの冒頭に述べたとおり、秘密鍵を持っていないためabGを計算することはできない。
長くなったが、できる限り数学の要素を排除して、コードも可読性を重視して書いてみたが、全て理解できずともイメージが掴めれば幸いである。
この記事が気に入ったらサポートをしてみませんか?
