努力と成長の関係を、無理やり数学的に説明するシリーズ第４弾です。

前回の記事は、こちらからどうぞ。

成長と努力のロジスティック曲線は、次のように表すことができました。

y ＝ K/{1＋α exp(−rx)}

前回まで、限界値 K の寄与ばかり考えたので、今度は初期値 P について考えてみます。
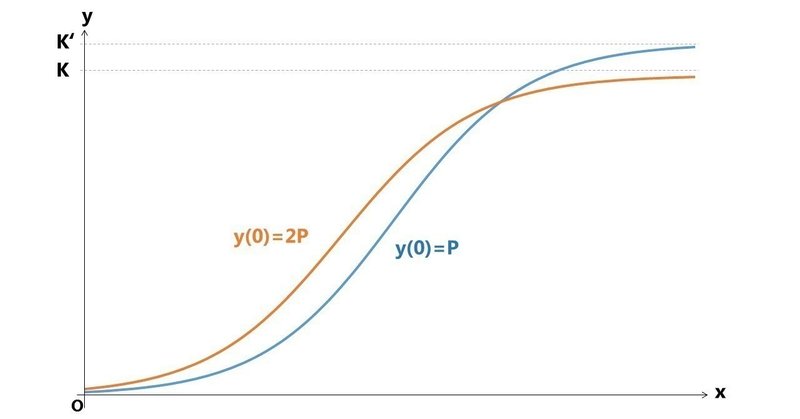
K と r は一定だとした場合、初期値 P が２倍になると、成長曲線は図のようになります。

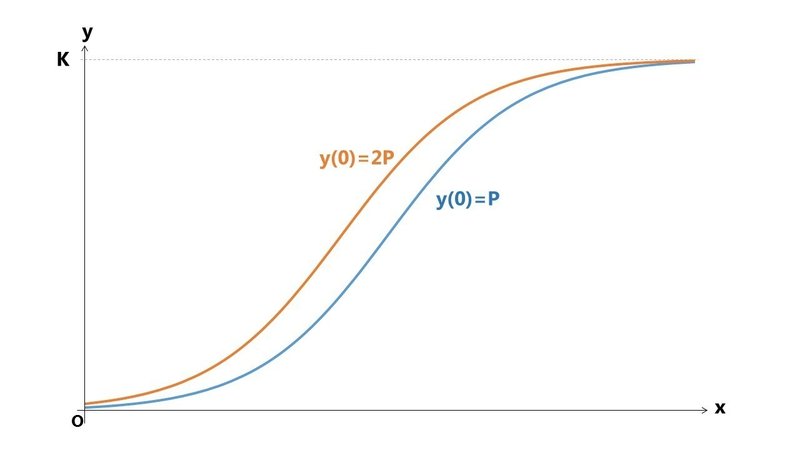
初期値は、生まれ持った先天的な才能だと捉えることができます。
はじめは小さな差ではありますが、同じような条件で同じだけ努力をしても、やはり元から才能がある人には、なかなか追いつけない感じがします。

では、A君が生まれつき能力の高いB君に追いつくための方法を考えます。
やはり、B君以上に必死で努力するのが良さそうです。

努力の密度を高める、例えば、B君より15％大きい係数 r で努力を続けるとこうなります。

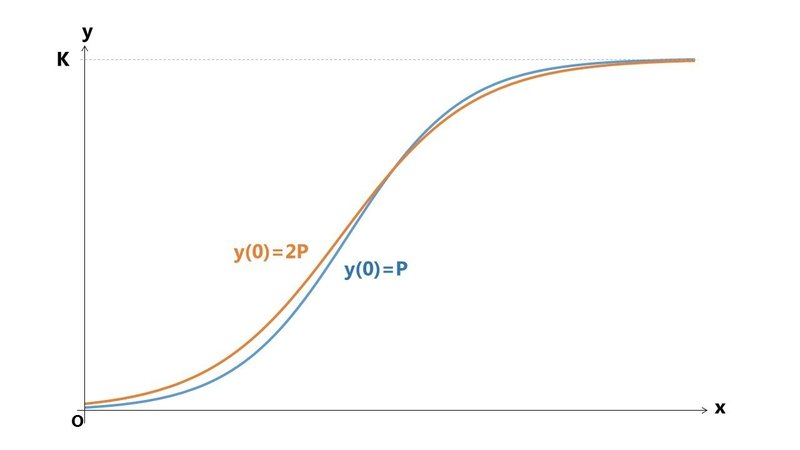
追い越しました。
全体的に、大きく差を広げられる場面も無いです。
天性の才能を持つ者に勝つためには、その人以上に、時間当たりの努力の量、ないしは努力の質を高める必要がありそうです。

次は、r をB君と同じに戻して、少しインチキみたいですが、限界値 K をB君の1.1倍に設定してみます。
戦い方や、戦う場所を、何かしら工夫したと思ってください。

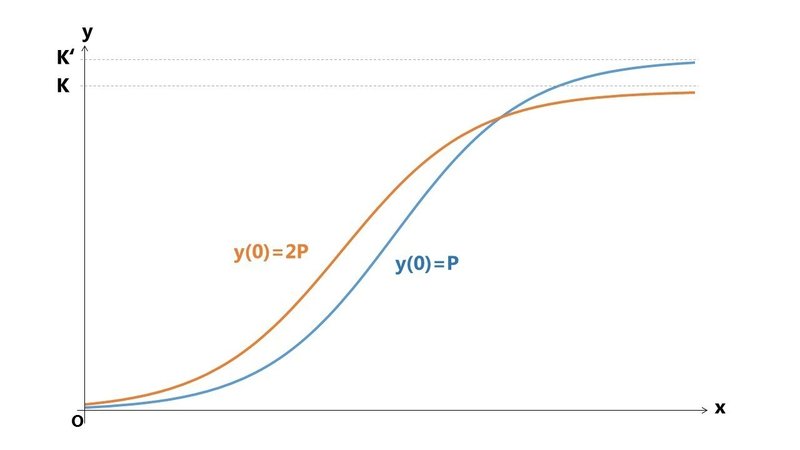
こちらももちろん追い越しましたが、案外追い越すポイントは後半になりました。
かなり長い間、差をつけられたままです。
生まれつきの才能恐るべしですね。
まあ、この辺の数字の設定は僕の匙加減でしかないんですが、あくまでもイメージです。

では、B君は生まれつきA君よりも初期能力が4倍も高かったのに、A君よりもいくらか遅れて努力を始めたとしましょう。
t = 0 から一定の時間の間、B君の Y をフラットにしてみます。

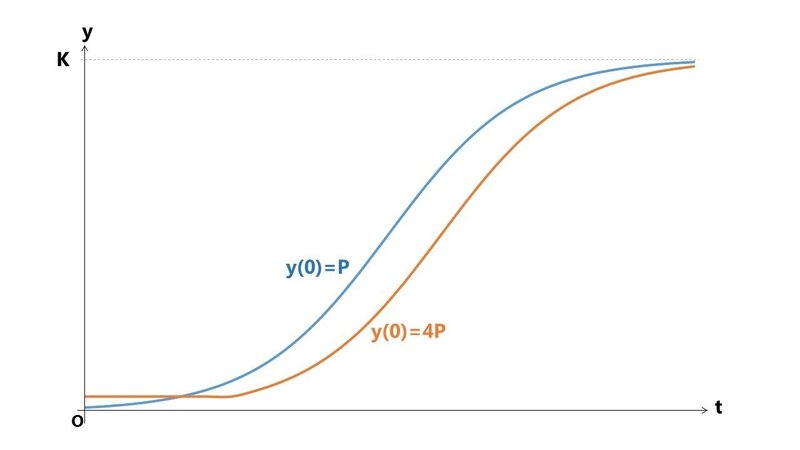
r と K は２人とも同じ条件で、y は時間 t の関数として表しています。
数式の成り立ちを考えれば当たり前なのですが、増加率 dy/dt はその時点での y に依存しているので、r や K が同じであれば、一度追い抜かれたら、初期値に関係なく追いつけません。

さらに、環境の変化に伴って K が減少していくとすると、到達できる最大値にすら差が出てしまいます。

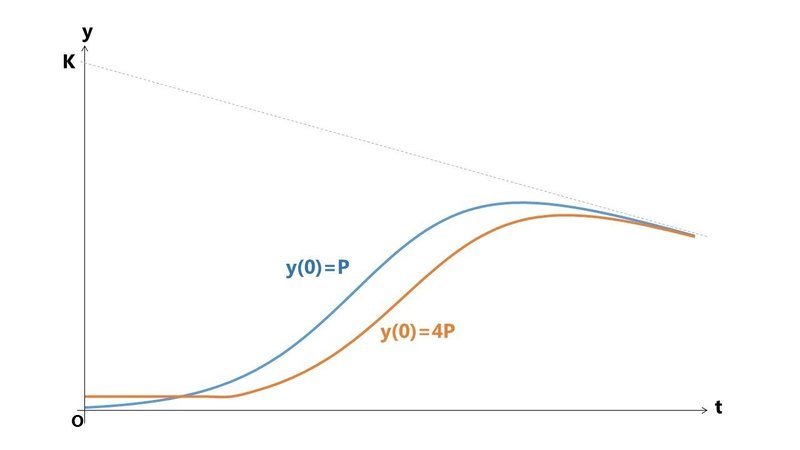
変化の激しい現代において、とにかく早くスタートすることは非常に重要です。
はじめはなかなか結果が出ませんが、例え初期値が高くなくても、誰よりも早く始めるということは、やがて大きなアドバンテージになりえます。

さて、４回に渡って努力と成長の関係を考えてみました。
理論的なのかこじつけなのかよく分からない考察で、正直どこまで議論を深められるか不安でしたが、書いている自分は面白かったので良しとします。

実際、こうして数式に落とし込んで考えてみると、これまで抽象的にしか説明できなかったいろんなことも、同じ理論に当てはめて説明できそうな気がします。

例えば、このスモールスタートの記事の、「小さく素早く始めるべきだが、あくまでトップを狙ってやるべき」という主張は、「K が小さいやり方のままでは、スピードがあってもすぐに成長が止まる」という風に、ロジスティック曲線を用いて説明できます。

自分のキャリアや、会社の戦略を考えるとき、今は成長曲線のどこにいるのか、今の条件での限界値はどの辺りにあるのか、その限界はどういう制約によってもたらされているか、そういうことをロジスティック関数に当てはめながら考えてみるのもいいんじゃないでしょうか。

まとめてみましたが、まだ続きます。
あと１回だけお願いします。

シンプルなくせに汎用性が高い数式が好きなんです。