この記事では、統計学のなかで、とても重要な概念である中心極限定理について、事例をまじえながら、分かりやすく説明していきます。

この記事を読むと、中心極限定理の概念や素晴らしさが理解できます。

中心極限定理とは

教科書的に言うと、以下の通りです。

これだと・・・・ですよね

そこで、ざっくり分かりやすく言うと

ということです。

初見の方は、この段階では、何となく便利そうだなということだけ実感できればいいと思います。

ここでは、「母集団がどんな分布であっても」というのがポイントです。

世の中の多くのデータの母集団は必ずしも正規分布ではありません。
サイコロの目のような一様分布や、コインの裏表のような二項分布など、実に多くあります。

中心極限定理によって、どんな分布であっても、標本平均は正規分布に近似することができます。これが素晴らしいのです

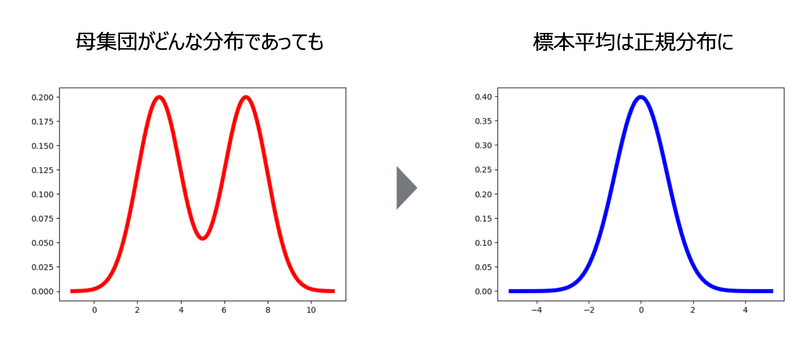
また、正規分布のカタチは、平均$${μ}$$、分散$${σ^2/n}$$になります。

中心極限定理のメリット

では、中心極限定理のメリットは何でしょうか？

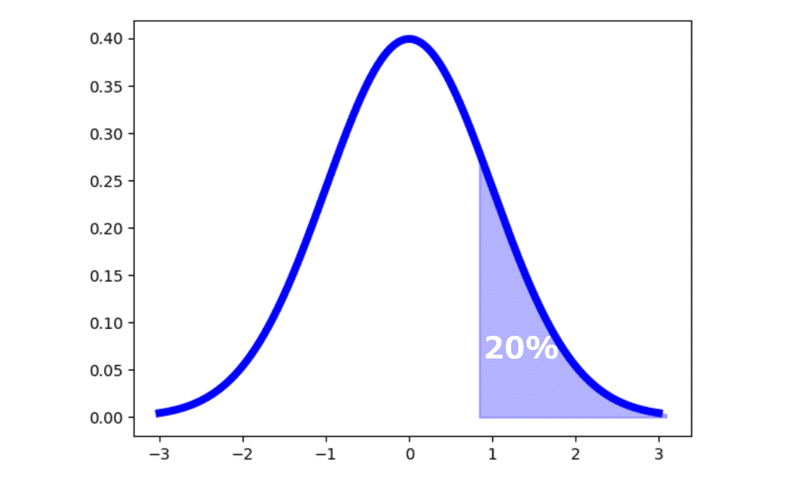
最大のメリットは、正規分布を使って、簡単に期待値や確率を計算できることです。

例題

具体的な例で考えてみましょう。

この事象は、成功確率1/6（5が出る）事象を30回試行しますので、成功回数Xは、二項分布（30, 1/6)に従います。

確率を式で表すと、次のとおりです。

$$
{}_{30} C_X  (\frac{1}{6})^X (\frac{5}{6})^{30-X}
$$

Xに10以上の数字を一つずつ代入していけば問題の答えとなりますが、とても大変です。
そこで中心極限定理を使って、正規分布に近似させます。

二項分布の成功確率の期待値はp、分散はp(1-p)ですので、
したがって、正規分布$${N(p, p(1-p)/n) = N(1/6, \frac{5}{36*30})}$$に近似できます。

この正規分布で、1/3(10÷3)以上になる確率を求めれば良いので、

$$
Z=(1/3-1/6)/\sqrt{\frac{5}{36*30}} = 2.45
$$

標準正規分布表より、確率は0.0071となります。

なお、二項分布の成功回数の期待値np、分散np(1-p)の考え方からいくと、そのまま正規分布$${N(np, np(1-p)) = N(5, 25/6)}$$に近似すると考えることもできます。この場合でも答えは同じになります。

まとめ

中心極限定理とは、大量のランダムな数値（例えば、たくさんのサイコロの目）の合計（または平均）は、どのような元の分布形状であっても、正規分布に近づくという定理です。

これは、自然界や社会現象など、さまざまな場面で見られる現象で、統計学の基礎となっています。
考え方をしっかりマスターして、実務で使えるようにしていきましょう！