（統計学的）機械学習による予測モデルの構築は主に以下の２つの作業によってなされます。

1. 予測モデルのアーキテクチャ（関数形）を設定
2. 実際のサンプリングデータと同様（もしくは近い）出力値が得られるように予測モデルのパラメータを調整

予測モデルのパラメータを調整をする際に登場するのが損失関数です。「実際のサンプリングデータと同様（もしくは近い）出力値が得られるように予測モデルのパラメータを調整」を「損失関数がより小さくなるようにパラメータを調整」に置き換えるわけです。損失関数は問題設定に応じて使い分けられるのが一般的です。例えば，回帰問題だったら二乗誤差，分類問題だったら交差エントロピーといった感じです。機械学習の参考書や説明記事ではこれらが天下り的に与えられることが多い印象がありますが，↓の参考書ではこれらの起源が統一的に説明されており，背後にあるモデル化への発想も分かりやすかったので，自分のメモ書きとして記したいと思います。

機械学習による予測モデルの背後にある概念

入力値xに対して出力値yがある，という状況を想定します。
次に，この(x,y)の背後には確率分布P(x,y)が存在し，(x,y)という値を得ることは確率分布P(x,y)からサンプリングを行っていることに等しい，と考えることにします。P(x,y)をデータ生成分布と称することにします。

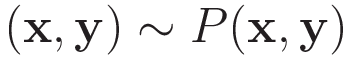
機械学習で行いことは，P(x,y)のモデル式を定義し，モデル式内の調整可能なパラメータを（半）機械的に調整することでP(x,y)にできる限り近づけることになります。P(x,y)のモデル式をQ(W;x,y)と表記することにします。Wはモデル式内の調整可能なパラメータを表します。
P(x,y)とQ(W;x,y)がより近い確率分布であるかを表す量としてKLダイバージェンスがあります。

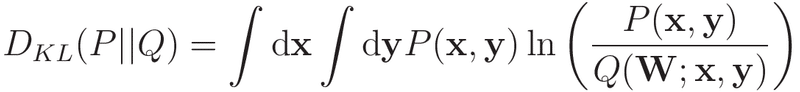
つまり，KLダイバージェンスが小さくなるようにWを調整することでQ(W;x,y)をP(x,y)に近づけることができるわけです。
xの実現確率はP(x,y)でもQ(W;x,y)でも同じとの仮定の下，上式を式変形すると以下のようになります。

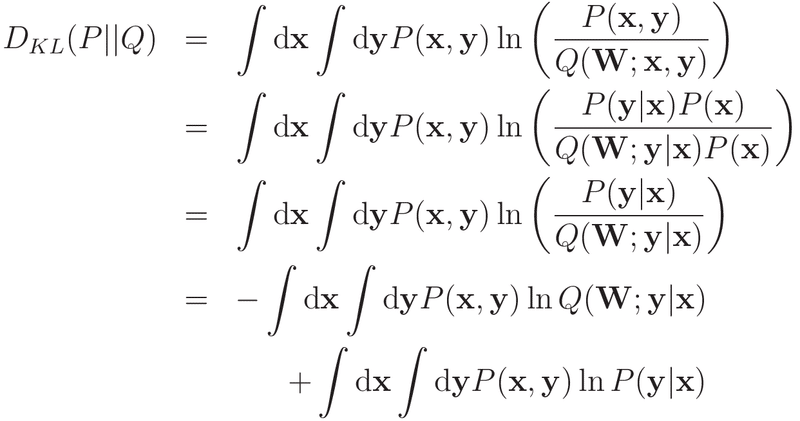
右辺の最後の表式の第2項はWを含んでいないため，学習対象外となります。そのため，損失関数は

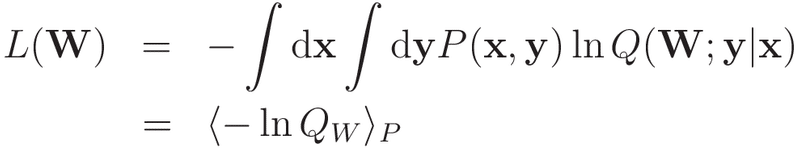
とすれば良さそうです。ですが，P(x, y)の具体的な表式が分からないと-ln(Q_w)の期待値を計算することができませんので，サンプリングデータを用いた平均値で代用することにします。

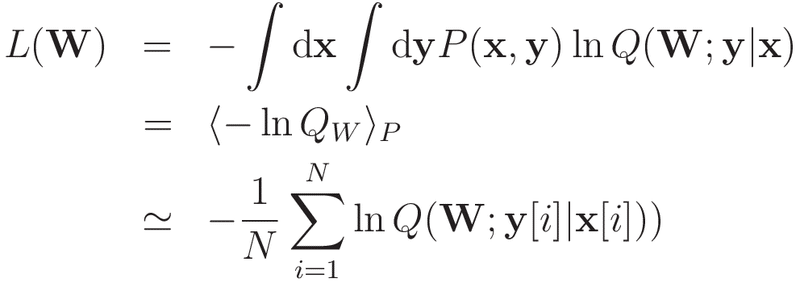
これまでの議論は回帰・分類問題に関わらず成立します。モデル分布Q(W;x,y)の具体的な表式に応じて，損失関数の具体的な表式も変化することになります。

（線形）回帰問題でのモデル分布と損失関数の表式

線形回帰モデル（入力層と出力層のみからなるニューラルネットワークモデルと置き換えても良いです）では，モデル分布をガウス分布で表現していることに等しいです。

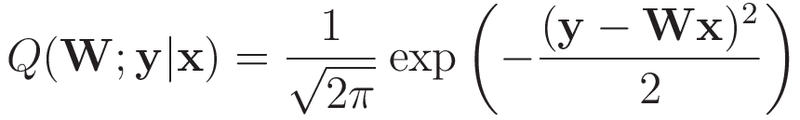
これに対する損失関数は

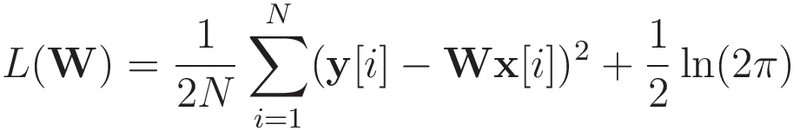
となり，平均二乗誤差と等価になります。

分類問題でのモデル分布と損失関数の表式

ここではカテゴリ数がMであり，m番目のカテゴリの分類をm番目の要素が1，それ以外の要素が0のベクトルで表すことにします。
モデル分布もM次元のベクトルで，かつ各要素が0から1の値を取るような関数が望ましいため，入力xを線形変換によってM次元のベクトルにし，かつ値が0から１になるように定義（例えば，ソフトマックス関数）することにします。

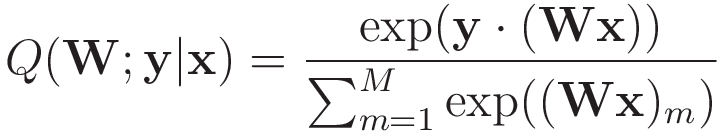
このとき損失関数は

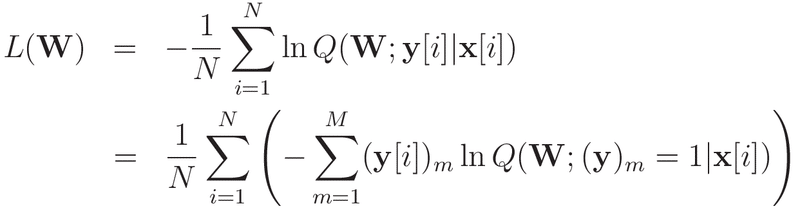
となります。

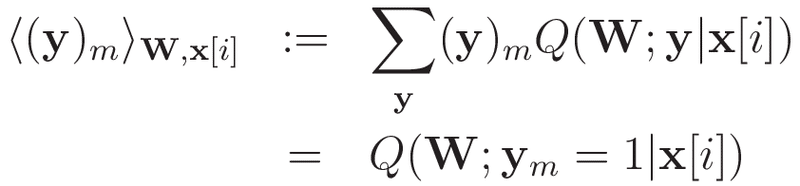
という表記を用いて整理すると，

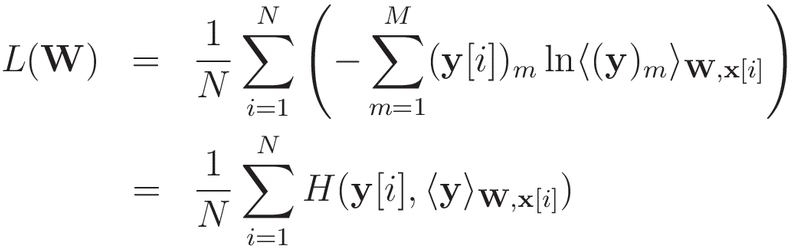
となり，交差エントロピーの平均値の表式を得ることができます。

ディープニューラルネットの場合はどうなのか？

上記の例は単純な線形変換（＋確率に対応付けるための活性化関数）であり，ディープニューラルネットの場合は入力値xに対する出力値yのモデル分布という意味でははるかに複雑な関数形となります。にも関わらず，ディープニューラルネットの場合においても同じ解釈を適用することができます。上記の単純な線形変換とディープニューラルネットの違いは，入力値xが幾つもの変換を経て加工された値に対する出力値yのモデル分布を考えているという点です。つまり，N層のディープニューラルネットのN-1層までは回帰or分類問題に都合の良いデータ加工の役割を担い，最後のN層においてデータ生成分布を模倣するモデル分布の役割を担うと解釈することができます。